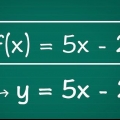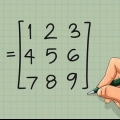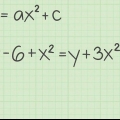Trouver l'inverse d'une matrice 3x3 : 6 étapes (avec photos)

Teneur

Pas
Des astuces
Mises en garde

Calculer l`inverse d`une matrice 3x3 à la main est une corvée fastidieuse. Mais c`est aussi utile et pas difficile, et cela aide à résoudre diverses équations matricielles.

Pas

1. Déterminer det(M), le déterminant de la matrice M. Le déterminant est généralement au dénominateur de l`inverse. Si le déterminant est égal à zéro, alors la matrice n`a pas d`inverse.

2. Déterminer M, la transposition de la matrice. Transposer signifie refléter la matrice dans la diagonale principale ou quoi que ce soit de identique, en échangeant l`élément (i,j) et l`élément (j,i).

3. Déterminer le déterminant de chacune des matrices mineures 2x2, les mineurs.

4. Affichez-le sous forme de matrice de cofacteurs comme indiqué et multipliez chaque terme par le signe indiqué.Le résultat de ces étapes est la matrice auxiliaire (parfois aussi la matrice auxiliaire), notée Adj(M).

5. Trouver l`inverse en divisant la matrice d`adjuvant trouvée à l`étape précédente par le déterminant de la première étape.

6. Ces étapes peuvent être combinées en transposant, en copiant sur les deux premières lignes et colonnes et en déterminant le déterminant 2x2 autour de chaque point. En vérifiant le travail, le déterminant est calculé de trois manières ; si ceux-ci correspondent, alors vous avez trouvé la bonne réponse. Avec le "torus" méthode, le signe est immédiatement correct.

Des astuces

Notez que la même méthode peut être appliquée à une matrice de variables et d`inconnues, par exemple une matrice algébrique, M, et son inverse, M.
Notez toutes vos étapes car il est très difficile de résoudre par cœur l`inverse d`une matrice 3x3. De plus, l`écriture garantit que vous faites des erreurs moins rapidement.
Il existe des programmes informatiques qui calculent les inverses d`une matrice pour vous. , jusqu`à une taille de matrices 30x30

La matrice adjuvantée est la transposition de la matrice des cofacteurs. C`est pourquoi nous transposons la matrice à l`étape 2, pour trouver une transposition d`une matrice de cofacteur.
Vérifiez s`il est correct en multipliant M par M. Vous devriez maintenant être en mesure de confirmer que M*M = M*M = I. I est la matrice unité, composée de uns le long de la diagonale principale et de zéros partout ailleurs. Sinon, tu as fait une erreur quelque part.

Mises en garde

Toutes les matrices 3x3 n`ont pas d`inverse. Si le déterminant de la matrice est 0, alors elle n`a pas d`inverse. (Notez que dans la formule on divise par det(M). La division par zéro n`est pas possible.)