Trouver l'angle entre deux vecteurs

Teneur

Pas
Des astuces

Les mathématiciens et les physiciens doivent souvent trouver l`angle entre deux vecteurs donnés. Bien qu`il soit facile de trouver l`angle entre deux vecteurs dans le même plan en graphique, cela peut être un peu plus délicat dans l`espace ou en trois dimensions. Cet article explique la méthode à utiliser pour trouver l`angle entre deux vecteurs dans le plan ou dans l`espace.

Pas

Méthode 1 sur 4: Déterminer les vecteurs

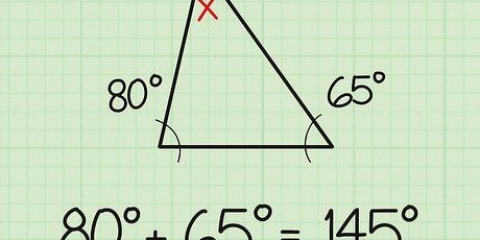
1. Déterminez les vecteurs dont vous avez besoin pour trouver l`angle. Prenons les deux vecteurs À et QO qui se coupent au point O, et calculez l`angle MOQ. Vous devez utiliser les vecteurs À et QO utiliser, ne pas MO ou QO. Dans le cas où MO est connu, multipliez-le par -1 pour obtenir À pour obtenir.

Méthode 2 sur 4: Trouver le produit scalaire

Trouver le produit scalaire (ou produit scalaire) des deux vecteurs. Si vous ne savez pas comment calculer le produit scalaire de deux vecteurs, lisez la suite :

1. Déterminer les composantes du vecteur dans chaque direction. Lorsque les vecteurs sont répertoriés dans un tableau, la première ligne représente généralement l`axe des x, la deuxième ligne représente l`axe des y et la troisième représente l`axe des z. Si le vecteur s`écrit sous la forme xje + ouij + zk, puis définissez les coefficients de je, yo, et k l`amplitude des composantes le long des axes x, y et z (je, yo, et k sont les vecteurs le long des axes x, y et z).

2. Multiplier les composantes des deux vecteurs le long de l`axe des x. Multipliez ensuite les composantes des deux vecteurs le long de l`axe y et faites de même pour les composantes le long de l`axe z.

3. Additionner les trois produits ensemble. C`est le produit scalaire des deux vecteurs. Le produit scalaire, ou "produit interne", de deux vecteurs est un nombre très utile en géométrie et en physique. Pour le moment nous n`utilisons ce produit que comme outil pour calculer l`angle entre deux vecteurs. Dans un vecteur à deux dimensions, la composante le long de l`axe z est nulle, donc le produit scalaire peut être trouvé en ne considérant que les composantes le long des axes x et y.

Méthode 3 sur 4: Calculer la taille

1. Calculer la magnitude des deux vecteurs. Calculer la magnitude des deux vecteurs, en utilisant la formule a=b+c+d, par lequel une est la grandeur du vecteur, et avant JC, et ré la taille des composants dans les trois directions différentes. Dans le plan plat ré être égal à zéro.

Méthode 4 sur 4: = Trouver l`angle

1. Utilisez les valeurs calculées ci-dessus dans cette formule : cosθ = a.b / |a||b|

2. Déduire le cosinus inverse de ce.

3. Fini.

Des astuces

Vous pouvez utiliser cette méthode pour calculer l`angle dans les graphiques 3D ou x-y-z en traitant les côtés comme des vecteurs et en traitant le vecteur comme des vecteurs libres.