Trouver le plus petit commun multiple de deux nombres

Teneur

Pas
Des astuces
Nécessités

Le plus petit commun multiple (KGB) d`un groupe de nombres est le plus petit nombre qui est un multiple de tous les nombres du groupe. Par exemple, le LCF de 16 et 20 est de 80 ; 80 est le plus petit nombre qui est à la fois un multiple de 16 et un multiple de 20. Vous pouvez trouver le LCF de deux nombres ou plus, en utilisant différentes méthodes. Si vous voulez savoir comment trouver le LCF de deux nombres ou plus, suivez ces étapes.

Pas

Méthode 1 sur 4: Factorisation en nombres premiers

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 1

1. Déterminer les facteurs premiers des deux nombres. C`est une méthode idéale pour les grands nombres. La première étape pour trouver le plus petit commun multiple de deux nombres à l`aide de cette méthode est la factorisation des deux nombres en nombres premiers multipliés pour obtenir ce nombre en tant que produit. Vous pouvez commencer par faire une liste de deux nombres (facteurs) multipliés ensemble pour produire ce nombre, puis les factoriser dans leurs facteurs premiers. Supposons que vous vouliez trouver le plus petit commun multiple de 20 et 42. Voici comment le factoriser. 20 = 2 x 2 x 542 = 2 x 3 x 7

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 2

2. Notez quel nombre premier apparaît le plus souvent dans les facteurs premiers de chaque nombre. Voici une liste des nombres qui apparaissent le plus souvent pour chaque nombre premier dans l`exemple précédent 2 → 2 fois3 → 1 fois5 → 1 fois7 → 1 fois

3. Multiplier tous les facteurs ensemble . Voici ce que vous devez faire pour trouver l`ECG de l`exemple :

2 x 2 x 3 x 5 x 7 = 420.

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 3Bullet1

Le LCF de 20 et 42 est de 420.

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 3Bullet2

Méthode 2 sur 4: Lister tous les multiples des deux nombres

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 5

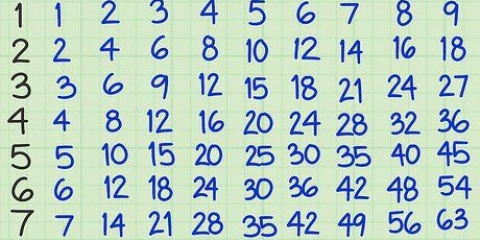
1. Lister quelques multiples du premier nombre dans l`ordre croissant. C`est une méthode idéale pour les petits nombres, en particulier pour les nombres inférieurs à 10. Pour de plus grands nombres, ce n`est pas recommandé car cela peut devenir difficile. Supposons que vous vouliez trouver le KGV de 5 et8. Vous faites d`abord une liste des multiples de 55 x 1 = 55 x 2 = 105 x 3 = 15

2. Lister maintenant quelques multiples du deuxième nombre (8), dans l`ordre croissant.

8x1 = 8

8x2 = 16

8x3 = 24

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 6

3. Essayez un certain nombre de possibilités pour les deux nombres, jusqu`à ce que vous ayez trouvé le plus petit commun multiple. Dans certains cas, vous pouvez trouver le LCF après quelques essais pour chaque numéro. Continuez dans cet exemple jusqu`à ce que vous trouviez le plus petit commun multiple pour 5 et 8. C`est ton kgf

5x4 = 20

5x5 = 25

5x6 = 30

5 x 7 = 35

5x8 = 40

8x4 = 32

8x5 = 40

Le LCF de 5 et 8 est de 40. C`est le multiple le moins commun car c`est un premier facteur du même multiple pour 5 et 8, et donc le LCF pour ces nombres.

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 6Bullet1

Méthode 3 sur 4: Utiliser une table de multiples communs

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 7

1. Écris les nombres en haut d`un tableau de multiples communs. Laissez un peu d`espace à gauche des chiffres et autant d`espace que possible en dessous des chiffres. Supposons que nous ayons les nombres 18, 12 et 30. Écrivez chaque nombre dans sa propre colonne, en haut du tableau.

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 8

2. Écris le facteur premier le moins commun des nombres dans l`espace de gauche. Recherchez le plus petit facteur premier (comme 2, 3 ou 5) que vous pouvez factoriser parmi tous les nombres. Ce sont tous des nombres pairs, donc au moins 2 est possible.

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 9

3. Divisez chacun des nombres que vous supposez par le facteur premier commun. Écris le quotient sous chaque nombre. Voici à quoi cela ressemblera :

18/2 = 9, donc écrivez 9 moins de 18 ans.

12/2 = 6, donc écrivez 6 sous 12.

30/2 = 15, donc écrivez 15 sous 30.

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 10

4. Répétez le processus de factorisation et de division par le facteur premier le plus bas jusqu`à ce qu`il ne reste plus de facteurs. Répétez pour les nombres 9, 6 et 15.

Facteur 3 de ces nombres. 3 est le plus petit facteur premier ici, le plus petit nombre premier divisible par les deux nombres.

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 10Bullet1

Divisez les trois nombres par 3 et écrivez le résultat en dessous de ces nombres.

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 10Bullet2

9/3 = 3, donc vous écrivez un 3 sous 9 ; 6/3 = 2, donc vous écrivez un 2 sous 6 ; 15/3 = 5 donc vous écrivez un 5 sous 15.

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 10Bullet3

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 11

5. Si deux des nombres partagent toujours un facteur premier commun, continuez cette procédure jusqu`à ce qu`aucun des nombres inférieurs n`ait de facteur commun. En ce qui concerne cet exemple, vous avez maintenant terminé.

Par exemple, supposons que les nombres du bas sont 2, 39 et 122, puis divisez 2 et 122 par 2, ce qui donne une nouvelle ligne du bas : 1, 39 et 61.

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 12

6. Multipliez tous les nombres de la première colonne par les facteurs premiers communs, par les nombres au bas de toutes les autres colonnes. C`est le KGV. Dans cet exemple, le produit de la colonne des facteurs communs est égal à 6 (2 x 3). Multipliez 6 par les nombres au bas des autres colonnes : 6 x 3 x 2 x 5 = 180.

Le LCF de 18, 12 et 30 est de 180.

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 12Bullet1

Méthode 4 sur 4: L`algorithme d`Euclide

1. Utilisez l`algorithme d`Euclide pour trouver le plus grand commun diviseur (GGD) de deux nombres. Supposons les deux nombres dans un exemple210 et 45 sont. Voici un exemple d`utilisation de l`algorithme d`Euclide pour trouver le GGD des deux nombres :

Divisez le premier nombre par le second : 210/45 = 4 (résidu 30). Cela signifie que 210 = 4 x 45 + 30.

Image intitulée Trouver le multiple le moins commun ou deux nombres Step 13Bullet1

Divisez ensuite le deuxième nombre (45) par le reste (30). 45/30 = 1 (reste 15). Donc 45 = 1 x 30 + 15.

Image intitulée Trouver le multiple le moins commun ou deux nombres Step 13Bullet2

Divisez ensuite le reste de la première étape (30) par le reste de la deuxième étape (15). 30/15 = 2 (résiduel 0). Donc 30 = 2 x 15 + 0.

Image intitulée Trouver le multiple le moins commun ou deux nombres Step 13Bullet3

Le GGD de 210 et 45 est de 15.

Image intitulée Trouver le multiple le moins commun ou deux nombres Step 13Bullet4

Vous pouvez toujours utiliser cette méthode pour trouver le GGD - arrêtez simplement de partager une fois que vous atteignez un reste de 0.

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 14

2. Multipliez les deux nombres originaux. 210 x 45 = 9 450

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 15

3. Divisez le résultat par le GGD des deux nombres. 9 450/15 = 630. 630 est le LCF de 210 et 45.

Image intitulée Trouver le multiple le moins commun ou deux nombres Étape 16

4. Utilisez l`algorithme d`Euclide pour trouver le LCF de trois nombres. Pour ce faire, recherchez simplement le PGCD de deux nombres, puis utilisez ce GGD pour trouver le VCF de ces deux nombres et le troisième nombre.

Des astuces

Si vous voulez savoir si le VCF est plus petit ou plus grand que le produit, utilisez cette méthode : si le GGD est 1, alors le VCF est le produit. Si le GGD est supérieur à 1, le VCGV sera plus petit que le produit.
Le KGV a de nombreuses applications. Le plus courant est que, lorsque vous additionnez ou soustrayez des fractions, elles doivent avoir le même dénominateur ; si ce n`est pas le cas, vous devrez les rendre éponymes, afin qu`ils aient le même dénominateur. La meilleure façon de le faire est de rechercher le plus petit dénominateur commun, qui est simplement le même que le LCF des dénominateurs. Par exemple, pour calculer 1/6 + 3/8, trouvons le LCF de 6 et 8, qui est 24, puis convertissons chaque fraction de sorte que les deux dénominateurs soient égaux à 24, laissant la somme comme ceci : 4/24 + 24/9. Nous pouvons maintenant calculer simplement cela, en additionnant le numérateur, avec la réponse : 13/24.
Si vous avez besoin de trouver le LCF de plus de 2 nombres, votre méthode ci-dessus devra changer légèrement car elle ne fonctionne que pour 2 nombres en même temps. Par exemple, pour trouver le LCF de 16, 20 et 32, on commence par trouver le LCF de 16 et 20 (qui vaut 80) puis le LCF de 80 et 32, qui sort à 160.
Par exemple, pour trouver les CHF de 16 et 20, on prend le GGD de 16 et 20, ce qui fait 4. 16 × 20 = 320 et 320 4 = 80, donc 80 est le KGV.
Si vous voulez faire une fraction du même nom, vous aurez besoin de savoir combien de fois chaque dénominateur va dans le LCF. En utilisant cette méthode, vous pouvez trouver le facteur de conversion en multipliant tous les nombres au bas de toutes les autres colonnes (sauf la première où tous les facteurs premiers sont répertoriés). Donc pour convertir 18 en 180, multipliez-le par 2 et 5. Pour convertir 12 en 180, multipliez-le par 3 et 5.Pour convertir 30 en 180, multipliez-le par 3 et 2.