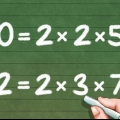Trouver le plus petit commun multiple de deux dénominateurs

Teneur

Pas
Nécessités

Pour additionner ou soustraire des fractions avec différents dénominateurs. il faut d`abord trouver le plus petit commun multiple de ces deux nombres. C`est le plus petit multiple de n`importe quel dénominateur dans une équation. Voici quelques méthodes différentes que vous pouvez utiliser pour trouver le lcm et les utiliser pour résoudre des problèmes de fraction.

Pas

Méthode 1 sur 4: Liste des multiples

Image intitulée Trouvez le plus petit dénominateur commun Étape 1

1. Lister les multiples de chaque dénominateur. Chaque liste doit comprendre le dénominateur de la fraction multiplié par 1, 2, 3, 4, etc.

Exemple : 1/2 + 1/3 + 1/5
Multiples de 2: 2 *1=2 ; 2 *2=4 ; 2 *3=6 ; 2 *4=8 ; 2 *5=10 ; 2 *6=12 ; 2 *7=14 ; etc.
Multiples de 3 : 3 *1=3 ; 3 *2=6 ; 3 *3=9 ; 3 *4=12 ; 3 *5=15 ; 3 *6=18 ; 3 *7=21 ; etc.
Multiples de 5 : 5 *1=5 ; 5 *2=10 ; 5 *3=15 ; 5 *4=20 ; 5 *5=25 ; 5 *6=30 ; 5 *7=35 ; etc.

Image intitulée Trouver le plus petit dénominateur commun, étape 2

2. Trouver le plus petit commun multiple. Parcourez chaque liste et mettez en surbrillance tout multiple commun des deux dénominateurs. Après avoir déterminé les multiples communs, déterminez quel est le plus petit.

Notez que s`il n`y a actuellement pas de multiple commun, vous devez continuer jusqu`à ce que vous trouviez un multiple valable pour les deux dénominateurs.

Exemple : 2 *15=30; 3 *10=30; 5 * 6=30

Le kgv=30

Image intitulée Trouvez le plus petit dénominateur commun, étape 3

3. Réécrire le problème d`origine. Pour écrire chaque fraction dans cette somme afin qu`elle ait la même valeur que le problème d`origine, il faut multiplier le numérateur et le dénominateur de la fraction par la valeur appropriée, qui correspond au multiple commun trouvé.

Exemple : 15 *(1/2); 10 *(1/3); 6 *(1/5)

Nouvelle somme : 15/30 + 10/30 + 6/30

Image intitulée Trouvez le plus petit dénominateur commun, étape 4

4. Résoudre. Une fois que vous avez trouvé le LCF et que les fractions ont été modifiées, vous devriez pouvoir résoudre ce problème sans aucun problème.

Exemple : 15/30 + 10/30 + 6/30=31/30=1 1/30

Méthode 2 sur 4: Utiliser le plus grand diviseur commun

Image intitulée Trouvez le plus petit dénominateur commun, étape 5

1. Trouver le plus grand diviseur commun de chaque dénominateur. Découvrez s`il existe un plus grand commun diviseur pour les deux dénominateurs en découvrant quels nombres sont divisibles par les dénominateurs.

Exemple : 3/8 + 5/12
Facteurs de 8 : 1, 2, 4, 8
Facteurs de 12 : 1, 2, 3, 4, 6, 12

Image intitulée Trouvez le plus petit dénominateur commun, étape 6

2. Identifier le plus grand diviseur commun entre les deux dénominateurs. Encerclez tous les PGCD après avoir trouvé les facteurs de chaque dénominateur. Le plus grand des PGCD est le plus grand dénominateur commun que vous pouvez utiliser pour résoudre davantage le problème.

Dans notre exemple, 8 et 12 partagent le dénominateur 1, 2 et 4.

Le plus grand diviseur commun est 4.

3. Multiplier les dénominateurs entre eux. Passez à l`étape suivante en multipliant les deux dénominateurs ensemble.

Exemple : 8 *12=96

Image intitulée Trouver le plus petit dénominateur commun Étape 7

4. Partage par le pgcd. Après avoir trouvé le produit des deux dénominateurs, divisez-le par le pgcd précédemment trouvé. Le résultat de cette division est votre plus petit commun multiple.

Exemple : 96 / 4=24

Image intitulée Trouver le plus petit dénominateur commun, étape 8

5. Réécrire le problème d`origine. Réécrivez les numérateurs en les multipliant par le même nombre qu`il a fallu pour que les dénominateurs correspondants soient égaux au lcg. Trouvez le facteur pour chaque fraction en divisant le lcm par le dénominateur d`origine.

Exemple : 24 / 8=3 ; 24 / 12=2

3 *(3/8)=9/24 ; 2 *(5/12)=10/24

24/9 + 24/10

Image intitulée Trouvez le plus petit dénominateur commun, étape 9

6. Résoudre le problème. Avec le kgv trouvé, il devrait maintenant être possible d`ajouter et de soustraire sans aucun problème.

Exemple : 9/24 + 10/24 = 19/24

Méthode 3 sur 4: Factorisation des fractions en facteurs premiers

Image intitulée Trouvez le plus petit dénominateur commun, étape 10

1. Diviser les dénominateurs en nombres premiers. Divisez chaque dénominateur en une série de nombres premiers. Rappelez-vous que les nombres premiers sont ces nombres qui ne peuvent être divisés par aucun autre nombre sauf 1 et lui-même.

Exemple : 1/4 + 1/5 + 1/12
Les facteurs premiers de 4: 2 * 2
Les facteurs premiers de 5: 5
Les facteurs premiers de 12 : 2 *2 *3

Image intitulée Trouver le plus petit dénominateur commun Étape 11

2. Compter le nombre de fois où chaque nombre premier apparaît dans l`ensemble des facteurs premiers. Turf le nombre de fois où chaque nombre premier apparaît dans les facteurs premiers de chaque dénominateur.

Exemple : il y a deux 2-et en 4 ; nul 2-et en 5 ; deux 2-et en 12

Il y a zéro 3-et en 4 et 5 ; une 3 en 12

Il y a zéro 5-et en 4 et 12; une 5 en 5

Image intitulée Trouver le plus petit dénominateur commun Étape 12

3. Prendre le plus grand nombre pour n`importe quel nombre premier. Notez combien de fois vous avez utilisé chaque nombre premier.

Exemple : le plus grand nombre pour 2 est deux ; le plus grand nombre pour 3 est un; le plus grand nombre pour 5 est un.

Image intitulée Trouver le plus petit dénominateur commun Étape 13

4. Écrivez ceci comme exemple ci-dessous.

Exemple : 2, 2, 3, 5

Image intitulée Trouver le plus petit dénominateur commun Étape 14

5. Multipliez tous les nombres premiers comme ceci. Multiplier les nombres premiers de la série précédente. Le produit de ces nombres est égal au lcm du problème d`origine.

Exemple : 2 *2 *3 *5=60

kgf=60

Image intitulée Trouvez le plus petit dénominateur commun Étape 15

6. Réécrire le problème d`origine. Divisez le LCF par le dénominateur original. Multipliez chaque numérateur par le même nombre nécessaire pour faire du dénominateur correspondant le LCF.

Exemple : 60/4=15 ; 60/5=12 ; 60/12=5

15 *(1/4)=15/60 ; 12 *(1/5)=12/60 ; 5 *(1/12)=5/60

15/60 + 12/60 + 5/60

Image intitulée Trouver le plus petit dénominateur commun Étape 16

sept. Résoudre. Avec le LCF trouvé et les dénominateurs similaires, il est devenu facile d`ajouter et de soustraire les fractions comme d`habitude.

Exemple : 15/60 + 12/60 + 5/60=32/60=8/15

Méthode 4 sur 4: Travailler avec des nombres entiers et des nombres mixtes

Image intitulée Trouver le plus petit dénominateur commun Étape 17

1. Convertir n`importe quel entier et nombre mixte en une fraction impropre. Convertir des nombres fractionnaires en fractions impropres en multipliant l`entier avant la fraction par le dénominateur et en ajoutant le numérateur au produit. Convertir un entier en une fraction impropre en le plaçant comme numérateur dans une fraction avec le dénominateur `1`.

Exemple : 8 + 2 1/4 + 2/3
8=8/1
2 1/4 ; 2 *4 + 1=8 + 1=9 ; 9/4
Mission réécrite : 8/1 + 9/4 + 2/3

Image intitulée Trouver le plus petit dénominateur commun Étape 18

2. Trouver le plus petit commun multiple des dénominateurs. Appliquer l`une des méthodes pour trouver le LCF d`une fraction commune, comme décrit ci-dessus. Notez que dans cet exemple, nous utilisons la méthode « Liste des multiples », en créant une liste de multiples pour chaque dénominateur et en dérivant le lcm de cette.

Notez que vous n`êtes pas obligé d`énumérer des multiples de 1 car tout nombre est un multiple de 1.

Exemple : 4 *1=4 ; 4 *2=8 ; 4 *3=12; 4 *4=16 ; etc.

3 *1=3 ; 3 *2=6 ; 3 *3=9 ; 3 *4=12; etc.

Le kgv=12

Image intitulée Trouver le plus petit dénominateur commun Étape 19

3. Réécrire le problème d`origine. Au lieu de simplement multiplier le dénominateur, il est nécessaire de multiplier également le numérateur par le nombre nécessaire pour faire du dénominateur un lcg.

Exemple : 12 *(8/1)=96/12 ; 3 *(9/4)=27/12 ; 4 *(2/3)=8/12

96/12 + 27/12 + 8/12

Image intitulée Trouver le plus petit dénominateur commun, étape 20

4. Résoudre le problème. Après avoir ajusté la fraction et trouvé le lcm dans le dénominateur, il devrait être facile d`ajouter et de soustraire les fractions sans aucun problème.

Exemple : 96/12 + 27/12 + 8/12=131/12=10 11/12