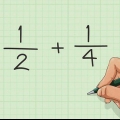Additionner et soustraire des fractions

Teneur

Additionner et soustraire des fractions est une compétence essentielle à apprendre. Vous rencontrez des fractions partout dans la vie de tous les jours, notamment en cours de maths, de l`école primaire à l`université. Suivez simplement les étapes ci-dessous pour apprendre à additionner et soustraire des fractions, qu`elles soient égales, inégales, mixtes ou impropres. Une fois que vous avez appris une façon, tout le reste est beaucoup plus facile!

Pas

Méthode 1 sur 3: Addition et soustraction de fractions avec le même dénominateur

$Image intitulée Ajouter et soustraire des fractions Étape 1$

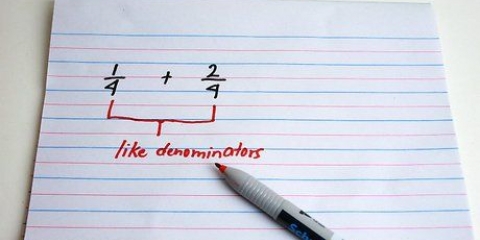
1. Écrire l`équation. Si le dénominateur des deux fractions que vous additionnez/soustrayez est le même, incluez également ce dénominateur dans votre réponse.

En d`autres termes, vous n`avez pas besoin d`écrire 1/5 et 2/5 comme 1/5 + 2/5 = ? Cela peut être noté comme (1+2)/5 = ?. Le dénominateur est le même et n`a donc besoin d`être mentionné qu`une seule fois. Les deux numérateurs sont au-dessus de la ligne de score.

$Image intitulée Ajouter et soustraire des fractions Étape 2$

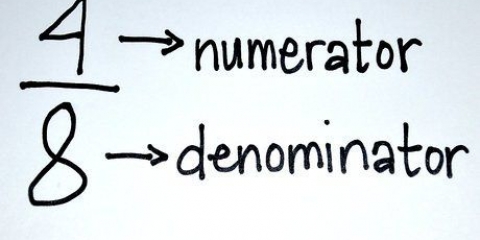
2. Additionner les compteurs ensemble. Le numérateur est le nombre au-dessus de la ligne de fraction. Prenons l`exemple suivant : 1/5 et 2/5 ; voici 1 et 2 nos compteurs.

Que vous écriviez 1/5 + 2/5 ou 1+2/5, la réponse est la même : 3! Enfin, 1 + 2 = 3.

$Image intitulée Ajouter et soustraire des fractions Étape 3$

3. Laisser le dénominateur inchangé. Rien à ajouter, soustraire, etc, mais inchangé.

Donc, en suivant le même exemple, le dénominateur est 5. C`est tout! C`est le nombre inférieur de la fraction et la moitié de la réponse!

$Image intitulée Ajouter et soustraire des fractions Étape 4$

4. Écrivez la réponse. Il ne vous reste plus qu`à écrire la réponse! Vous verrez que d`après l`exemple précédent, la réponse est 3/5.

Quel était le compteur? 3. Et le dénominateur? 5. Donc, 1/5 + 2/5, ou 1+2/5, égale 3/5.

Méthode 2 sur 3: Addition et soustraction de fractions avec différents dénominateurs

$Image intitulée Ajouter et soustraire des fractions Étape 5$

1. Trouver le plus petit commun multiple (LCM) des dénominateurs. C`est le plus petit nombre que les deux dénominateurs ont en commun. Prendre les fractions 2/3 et 3/4. Quels sont les dénominateurs? 3 et 4. Pour trouver le LCF des deux, utilisez l`une des 3 méthodes suivantes :

Notez les multiples. Les multiples de 3 sont 3, 6, 9, 12, 15, 18...et ainsi de suite. Les multiples de 4? 4, 8, 12, 16, 20, etc. Quel est le plus petit nombre qui se produit dans les deux ensembles ?? 12! C`est votre multiple le moins commun ou votre kgv.
Factorisation en facteurs premiers. Si vous savez ce que sont les facteurs premiers, vous pouvez utiliser la factorisation. Ici, vous déterminez avec quels nombres premiers vous pouvez multiplier un certain nombre au moyen de la multiplication "faire". Pour 3, les facteurs sont 3 et 1. Pour 4, les facteurs premiers sont 2 et 2. Ensuite, vous les multipliez ensemble, donc 3 x 2 x 2 = 12. votre kgf!

Multipliez les deux nombres pour obtenir lePetit Nombres. Dans certains cas, comme celui-ci, vous pouvez simplement multiplier les deux nombres ensemble - 3 x 4 = 12. Mais si vos dénominateurs sont de grands nombres, cela ne peut pas arriver! Vous ne pouvez pas simplement faire 56 x 44 et passer à 2464 comme réponse! Ce n`est pas mal, mais c`est gênant.

$Image intitulée Ajouter et soustraire des fractions Étape 6$

2. multipliez le dénominateur par le nombre dont vous avez besoin pour obtenir le lcg. En d`autres termes, vous voulez que chaque dénominateur soit le même nombre - le kgv. Pour notre exemple, cela doit être 12. 4x3 = 12. C`est le dénominateur de notre réponse finale.

Donc 2/3 devient 2/3 x 4 et 3/4 devient 3/4 x 3. Cela signifie que nous avons maintenant 2/12 et 3/12. Mais nous n`avons pas encore fini!

Vous remarquerez que dans ce cas, les dénominateurs ont été multipliés ensemble. Cela fonctionne dans cette situation, mais pas toujours. Parfois, vous devrez chercher des nombres plus petits pour trouver le LCF.

Et dans d`autres cas, avec des petits nombres, il suffit de multiplier les dénominateurs entre eux.

$Image intitulée Ajouter et soustraire des fractions Étape 7$

3. Multipliez également le numérateur par ce nombre. Si vous multipliez le dénominateur d`une fraction par un nombre, vous devrez également multiplier le numérateur par le même nombre. Ce que nous avons fait dans la dernière étape n`était qu`une partie de la multiplication nécessaire.

Nous avions 2/3x4 et 3/4x3 comme première étape - pour ajouter la deuxième étape, c`est en fait 2 x 4/3 x 4 et 3 x 3/4 x 3. Cela signifie que 8/12 et 9/12 sont nos nouveaux numéros. Parfait!

$Image intitulée Ajouter et soustraire des fractions Étape 8$

4. Additionnez (ou soustrayez) les numérateurs pour obtenir votre réponse. Pour additionner 8/12 à 9/12, il suffit d`additionner les numérateurs. N`oubliez pas : vous laissez le dénominateur seul. Le nombre que vous avez obtenu avec le LCF est votre dénominateur final.

Dans cet exemple : 8+9/12 = 17/12. Pour convertir cela en un nombre mixte, soustrayez le dénominateur du numérateur et voyez ce qu`il vous reste. Soit, dans ce cas, 17/12 = 1 5/12

Méthode 3 sur 3: Ajouter et soustraire des fractions mixtes et impropres

$Image intitulée Ajouter et soustraire des fractions Étape 9$

1. Convertissez vos fractions mixtes en fractions impropres. Une fraction mixte est un nombre entier suivi d`une fraction, comme dans l`exemple ci-dessus (1 5/12). Une fraction impropre est une fraction avec un numérateur plus grand que le dénominateur. Un exemple de ceci est 17/12.

Comme exemple nous prenons 13/12 et 17/8.

$Image intitulée Ajouter et soustraire des fractions Étape 10$

2. Trouver le dénominateur commun. Rappelez-vous les trois façons de trouver le lcg des dénominateurs? En déterminant les multiples, en utilisant des facteurs premiers ou en multipliant les dénominateurs entre eux.

Déterminons quels sont les multiples de 12 et 8. Quel est le plus petit nombre dans lequel les deux nombres correspondent ?? 24. 8, 16, 24 et 12, 24 – bingo!

$Image intitulée Ajouter et soustraire des fractions Étape 11$

3. Multipliez les numérateurs par les dénominateurs pour obtenir la fraction égale. Les deux dénominateurs doivent maintenant être convertis en 24. Comment faire 24 sur 12? Multipliez-le par 2. De 8 à 24? Multipliez-le par 3. Mais n`oubliez pas qu`il faut aussi multiplier les numérateurs!

Donc 13 x 2/12 x 2 = 26/24. Et 17 x 3/8 x 3 = 51/24. Nous avons parcouru un long chemin pour résoudre le problème!

$Image intitulée Ajouter et soustraire des fractions Étape 12$

4. Addition et soustraction de fractions. Maintenant que les deux fractions ont le même dénominateur, vous pouvez facilement ajouter ou soustraire les deux fractions. Rappelez-vous, laissez le dénominateur seul!

26/24 + 51/24 = 77/24. C`est la pause que tu cherchais! Mais le compteur est assez grand....

$Image intitulée Ajouter et soustraire des fractions Étape 13$

5. Transformez votre réponse en fraction mixte. Un numérateur aussi grand est un peu étrange et rend difficile de se faire une idée de la taille de votre fraction. Tout ce que vous avez à faire pour résoudre ce problème est de diviser le numérateur par le dénominateur et d`utiliser le reste comme numérateur pour votre nouvelle fraction composée.

Pour cet exemple : 24 va dans 77 . 3 fois.Donc, 24 x 3 = 72. Il reste alors un reste de 5! Alors quelle est votre réponse finale? 3 5/24. C`est tout!