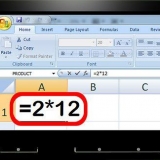
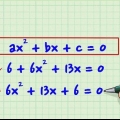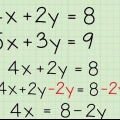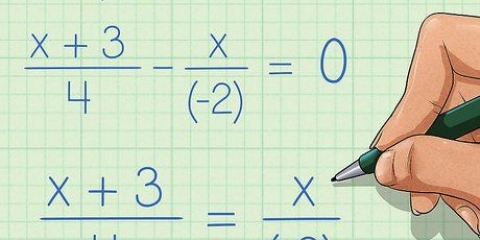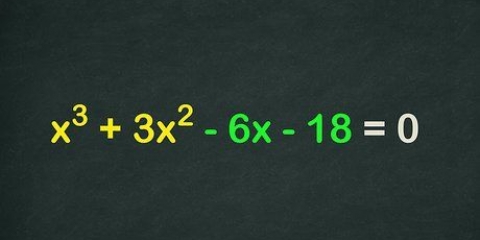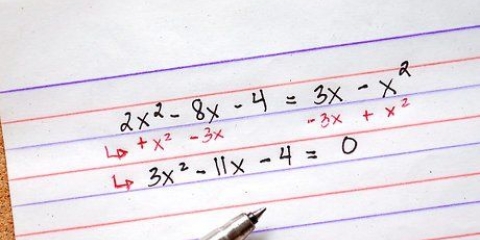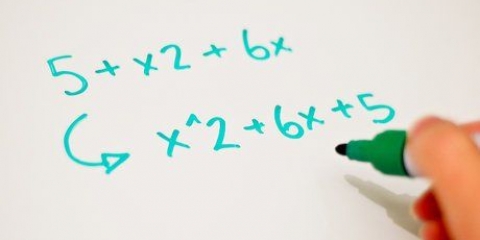Par exemple, la variable 12y peut être réécrite comme le produit des facteurs de 12 et y. Nous pouvons écrire 12y comme 3(4y), 2(6y), etc., en utilisant les facteurs de 12 qui sont les plus pratiques. On peut même aller jusqu`à 12 ans plusieurs fois dissoudre. En d`autres termes, nous n`avons pas à nous arrêter à 3(4y) ou 2(6y) - nous pouvons factoriser 4y et 6y en 3(2(2y) et 2(3(2y) respectivement). Apparemment ces deux expressions sont équivalentes. 
Essayons un exemple de problème. Pour factoriser l`équation 12x + 6, on cherche d`abord le pgcd de 12x et 6. 6 est le plus grand nombre qui divise à la fois 12x et 6, nous pouvons donc simplifier l`équation à 6(2x + 1). Ce processus s`applique également aux équations impliquant des nombres négatifs et des fractions. x/2 + 4, par exemple, peut être simplifié en 1/2(x + 8) et -7x + -21 peut être factorisé en -7(x + 3). 

Par exemple, prenons l`équation quadratique x + 5x + 6 = 0. Puisque 3 x 2 = 6 et 3 + 2 = 5, l`équation simplifiée devient (x + 3)(x + 2). De légères variations sur cette solution rapide simple peuvent être trouvées dans l`équation elle-même : Si l`équation quadratique est sous la forme x-bx+c, alors votre réponse ressemblera à ceci : (x - _)(x - _). Si de la forme x+bx+c, votre réponse ressemblera à ceci : (x + _)(x + _). Si de la forme x-bx-c, votre réponse ressemblera à ceci : (x + _)(x - _). Remarque : Les blancs peuvent être des fractions ou des décimales. Par exemple, l`équation x + (21/2)x + 5 = 0 se transforme en (x + 10)(x + 1/2). 
Élaborons un exemple de devoir. 3x - 8x + 4 semble un peu intimidant au début. Mais si nous nous rendons compte que 3 n`a que deux facteurs (3 et 1), alors cela devient beaucoup plus facile, car nous savons que notre réponse doit être de la forme (3x +/- _)(x +/- _). Dans ce cas, entrer -2 dans les blancs donnera la bonne réponse. -2 × 3x = -6x et -2 × x = -2x. -6x + -2x = -8x. -2 × -2 = 4, nous voyons donc que les termes pris en compte entre parenthèses multipliés ensemble, ont l`équation d`origine comme produit. 
Par exemple, l`équation x + 6x + 9 satisfait cette forme. 3 est 9 et 3 × 2 est 6. On sait donc que les facteurs de cette équation sont égaux à (x + 3)(x + 3) ou (x + 3). 
Revenons à l`équation x + 5x + 6 = 0. L`équation résolue est (x + 3)(x + 2) = 0. Si l`un de ces facteurs est égal à 0, alors toute l`équation est 0, donc les réponses possibles pour x sont les nombres où (x + 3) et (x + 2) sont égaux à 0. Ces nombres sont respectivement -3 et -2. 
On applique -2 et -3 à x + 5x + 6 = 0. Tout d`abord : -2 : (-2) + 5(-2) + 6 = 0 4 + -10 + 6 = 0 0 = 0. C`est correct, donc -2 est une réponse valide. Essayons maintenant -3 : (-3) + 5(-3) + 6 = 0 9 + -15 + 6 = 0 0 = 0. Ceci est également correct, donc -3 est également une réponse valide. 

L`équation 4x + 8xy + 4y peut être réécrite comme 4x + (2 × 2 × 2)xy + 4y. Maintenant, il devient clair qu`il est sous la forme correcte, de sorte que nous pouvons affirmer avec une certaine confiance que notre équation peut être prise en compte (2x + 2y). 
Par exemple : 8x - 27y peut être pris en compte dans (2x - 3y)(4x + ((2x)(3y)) + 9y).
Équations de factorisation
Teneur
En mathématiques, c`est factoriser déterminer des nombres ou des expressions qui, lorsqu`ils sont multipliés ensemble, donnent une valeur ou une équation particulière. L`affacturage est une compétence utile à apprendre lors de la résolution de problèmes mathématiques simples ; la capacité à factoriser correctement devient presque essentielle lorsqu`il s`agit d`équations quadratiques et d`autres polynômes. La factorisation peut être utilisée pour simplifier des équations mathématiques simples afin de faciliter leur résolution. L`affacturage peut vous permettre d`exclure vous-même des réponses possibles beaucoup plus rapidement que si vous deviez vérifier chacune d`entre elles.
Pas
Méthode 1 sur 3: Factorisation des nombres et des équations simples

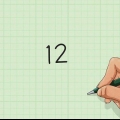
1. Comprendre la définition de la factorisation des nombres. La factorisation est simple en principe, mais en pratique, elle peut être assez difficile lors de la résolution d`équations complexes. Par conséquent, l`approche la plus simple consiste à commencer avec de petits nombres puis des équations simples avant de passer à des applications plus avancées. le les facteurs d`un nombre donné sont les nombres qui, multipliés ensemble, donnent ce nombre unique. Par exemple, les facteurs de 12 sont 1, 12, 2, 6, 3 et 4, car 1 × 12, 2 × 6 et 3 × 4 ont tous 12 comme produit.
- Une autre façon de penser est que les facteurs d`un nombre donné sont les nombres qui font le nombre dans peut être partagé dans son intégralité.
- Pouvez-vous trouver tous les facteurs de 60? Nous utilisons le nombre 60 pour diverses applications (le nombre de minutes dans une heure, de secondes dans une minute, etc.) car il est divisible par un grand nombre de nombres.
- Les facteurs de 60 sont 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 et 60.

2. Comprendre que les équations peuvent aussi être factorisées. Tout comme les nombres, les variables avec des coefficients peuvent également être factorisées. Vous faites cela en trouvant les facteurs du coefficient de la variable. Savoir comment factoriser les variables est utile pour simplifier les équations dont les variables font partie.

3. Appliquer la propriété distributive de la multiplication à la factorisation d`équations mathématiques. En utilisant vos connaissances sur la façon de factoriser à la fois des nombres réguliers et des variables avec des coefficients, vous pouvez également simplifier les équations mathématiques en déterminant les facteurs communs aux nombres et aux variables dans une équation mathématique. Habituellement, nous simplifierons l`équation autant que possible, en recherchant le plus grand diviseur commun (pgcd). Ce processus de simplification est possible en raison de la propriété distributive de la multiplication, qui stipule que pour tout nombre a, b et c, a(b + c) = ab + ac.
Méthode 2 sur 3: Factorisation des équations quadratiques

1. Assurez-vous que l`équation est sous forme quadratique (ax + bx + c = 0). les équations quadratiques sont de la forme ax + bx + c = 0, où a, b et c sont des constantes numériques et a n`est pas égal à 0 (notez que a est égal à pouvez sont sur 1 ou -1). Si vous avez affaire à une équation avec une variable (x) et un ou plusieurs termes de x au carré, vous pouvez généralement échanger les termes de l`équation en utilisant une opération mathématique standard pour obtenir 0 d`un côté de l`équation. signe et hache, etc. d`autre part.
- Par exemple, vous avez l`équation mathématique suivante : 5x + 7x - 9 = 4x + x - 18 qui peut être simplifiée en x + 6x + 9 = 0, sous la forme quadratique.
- Équations avec de plus grandes puissances de x, telles que x, x, etc. ne sont pas des équations quadratiques. Ce sont des équations cubiques ou supérieures, à moins que l`équation puisse être simplifiée de sorte que les termes avec des puissances de x plus élevées (que les carrés) soient éliminés.

2. Dans les équations quadratiques où a = 1, vous factorisez en (x+d )(x+e), où d × e = c et d + e = b. Si votre équation quadratique est sous la forme x + bx + c = 0 (en d`autres termes, si le coefficient de x = 1), alors il est possible (mais pas certain) qu`un raccourci relativement simple puisse être utilisé pour factoriser l`équation. Trouvez deux nombres qui ont tous deux c comme produit et additionnez-les pour obtenir b comme somme. Si vous avez ces deux nombres d et e, mettez-les dans l`expression suivante : (x+d)(x+e). Ces deux termes, lorsqu`ils sont multipliés, vous donnent l`équation quadratique - en d`autres termes, ce sont les facteurs de votre équation quadratique.

3. Si possible, vous pouvez également dissoudre les facteurs en regardant simplement de près. Croyez-le ou non, vous pouvez résoudre des équations quadratiques simples simplement en examinant attentivement le problème, puis en pesant les réponses possibles jusqu`à ce que vous trouviez la bonne. En d`autres termes, décomposez-vous en facteurs en essayant. Si l`équation est de la forme ax+bx+c et a>1, alors les termes seront de la forme (dx +/- _)(ex +/- _), où d et e sont des constantes, supérieures à zéro, qui multipliées ensemble ont a comme produit. D et e (ou les deux) pouvoir, capacité égal à 1, mais ce n`est pas toujours le cas. Si les deux sont à 1, alors vous avez essentiellement utilisé la méthode rapide décrite ci-dessus.

4. Résoudre cela en mettant au carré. Dans certains cas, les équations quadratiques peuvent être factorisées rapidement et facilement en utilisant une propriété mathématique spéciale. Toute équation quadratique de la forme x + 2xh + h = (x + h). Donc, si dans votre équation la valeur de b est le double de celle de la racine carrée de c, alors votre équation peut être factorisée en (x + (sqrt(c))).

5. Utiliser des facteurs pour résoudre des équations quadratiques. Quelle que soit la façon dont vous factorisez une équation quadratique ; une fois qu`il est pris en compte, vous pouvez trouver les réponses possibles pour la valeur de x en définissant chaque facteur égal à zéro et en le résolvant. Puisque vous recherchez des valeurs pour x où votre équation est nulle, une valeur pour x qui rend l`un ou l`autre des facteurs égal à zéro sera la réponse possible de votre équation quadratique.

6. Vérifiez vos réponses - certaines d`entre elles peuvent être incorrectes! Une fois que vous avez trouvé les réponses possibles pour x, appliquez-les à votre équation d`origine pour voir si elles sont valides. Parfois, les réponses que vous trouverez seront l`équation originale ne pas rendre égal à zéro lorsque vous les appliquez. Ces réponses sont Incorrect et nous les ignorons.
Méthode 3 sur 3: Factorisation d`autres formes d`équations

1. Si l`équation est de la forme a-b, alors les termes factorisés sont (a+b)(a-b). Les équations de deux variables sont résolues différemment des équations quadratiques. Pour toute équation a-b où a et b ne sont pas égaux à 0, les facteurs de l`équation sont (a+b)(a-b).
- Par exemple, l`équation 9x - 4y = (3x + 2y)(3x - 2y).

2. Si l`équation est de la forme a+2ab+b, décomposez-la en (a+b). Remarque : pour a le trinôme de la forme a-2ab+b, la forme dissoute est légèrement différente : (a-b).

3. Si l`équation est de la forme a-b, alors vous la décomposez en (a-b)(a+ab+b). Enfin, il convient de mentionner que les équations cubiques et les polynômes supérieurs peuvent également être factorisés, bien que ce processus devienne rapidement irréalisable.
Des astuces
- a-b peut être factorisé, mais a+b ne peut pas.
- Apprenez à factoriser des constantes - cela peut aider.
- Faites attention aux fractions pendant la factorisation et calculez-les correctement et soigneusement.
- Si vous avez un trinôme de la forme x+bx+ (b/2), alors la forme factorisée est (x+(b/2)) (vous pouvez rencontrer cela avec une formule carrée).
- Rappelez-vous que a x 0 = 0.
Nécessités
- Papier
- Crayon
- Livre de maths (si besoin)
Articles sur le sujet "Équations de factorisation"
Оцените, пожалуйста статью
Populaire