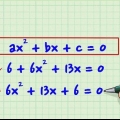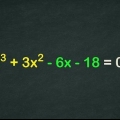→
→ 
 →
→ 
 →
→ 
Notez comment les signes moins restent devant le 2. Lorsqu`un terme est soustrait, le signe moins reste devant lui. 
Devoir d`exercice : .
. Facteurs de 3:1, 3 Facteurs de 6 : 1, 2, 3, 6. `Le plus grand diviseur commun est 3`. 
Devoir d`exercice : .
. Trouvez les plus grands diviseurs communs : 3 Pour supprimer le facteur des deux termes :

Devoir d`exercice :
Trouvez les plus grands diviseurs communs : 3 Pour supprimer le facteur des deux termes :
Multiplier le facteur par une nouvelle expression :
Réponse finale dissoute : 

Pour réorganiser les conditions :
Trouver le plus grand diviseur commun :
Pour supprimer le facteur des deux termes :
Multiplier le facteur par une nouvelle expression :
Vérifier la réponse:


Devoir d`exercice :
Égal à zéro :


Devoir d`exercice :
Égal à zéro :
Dissoudre:

Devoir d`exercice :
Égal à zéro :
Dissoudre:
Rendez les deux termes égaux à zéro 0 : 




y = 0 

y = 4 


 Cette réponse est correcte
Cette réponse est correcte

 Cette réponse est également correcte.
Cette réponse est également correcte.

Mission d`origine :
Pour réorganiser les conditions :
Pour fusionner des termes similaires :
Trouvez les plus grands diviseurs communs :
Dissoudre:

La formule de la différence des carrés parfaits :
Devoir d`exercice :
Déterminer les racines carrées : 

Appliquer des racines carrées à la formule : 

Formule pour la différence des puissances tierces :
Devoir d`exercice :
Déterminer les racines cubiques : ![Binômes de factorisation {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Binômes de factorisation {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Appliquez des cubes à la formule : 

Formule pour la somme des cubes parfaits :
Devoir d`exercice :
Déterminer les racines cubiques : ![Binômes de factorisation {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Binômes de factorisation {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Appliquez les cubes à la formule : 
Binômes de factorisation
Teneur
En algèbre, les binômes sont des expressions à deux termes reliées par un signe plus ou moins, telles que 
Pas
Partie 1 sur 3: Factorisation des binômes

1. Revoir les bases de l`affacturage. L`affacturage divise un grand nombre en ses diviseurs les plus simples. Chacune de ces parties est appelée un « facteur ». Par exemple, le nombre 6 est divisible par quatre nombres différents : 1, 2, 3 et 6. Donc 1, 2, 3 et 6 sont les facteurs de 6.
- Les facteurs de 32 sont 1, 2, 4, 8, 16 et 32
- « 1 » et le nombre que vous factorisez sont toujours des facteurs. Donc les facteurs d`un petit nombre comme 3 sont juste 1 et 3.
- Les facteurs ne sont que les nombres entièrement divisibles, c`est-à-dire les nombres « entiers ». Vous pouvez diviser 32 par 3,564 ou 21,4952, mais ce ne sont pas des facteurs, juste des nombres décimaux.

2. Lister les termes du binôme pour en faciliter la lecture. Un binôme n`est rien d`autre que l`addition ou la soustraction de deux termes, dont au moins un contient une variable. Parfois, ces variables ont des exposants, tels que  ou
ou  . Si vous essayez de factoriser des binômes pour la première fois, il est utile d`ordonner les équations en termes de variables décroissantes, ce qui signifie que le plus grand exposant vient en dernier. Par exemple:
. Si vous essayez de factoriser des binômes pour la première fois, il est utile d`ordonner les équations en termes de variables décroissantes, ce qui signifie que le plus grand exposant vient en dernier. Par exemple:
 ou
ou  . Si vous essayez de factoriser des binômes pour la première fois, il est utile d`ordonner les équations en termes de variables décroissantes, ce qui signifie que le plus grand exposant vient en dernier. Par exemple:
. Si vous essayez de factoriser des binômes pour la première fois, il est utile d`ordonner les équations en termes de variables décroissantes, ce qui signifie que le plus grand exposant vient en dernier. Par exemple: →
→ 
 →
→ 
 →
→ 

3. Trouver le plus grand diviseur commun des deux termes. Cela signifie que vous recherchez le plus grand nombre par lequel les deux parties du binôme sont divisibles par. Si cela ne fonctionne pas, factorisez les deux nombres séparément et voyez quel est le nombre correspondant le plus élevé. Par exemple:
 .
.
4. Divisez le plus grand diviseur commun pour chaque terme. Si vous connaissez le dénominateur commun, vous devez le supprimer de chaque terme. Notez que vous divisez simplement les termes en faisant de chacun un problème de division plus petit. Si cela est fait correctement, les deux équations ont le même facteur :
 .
.

5. Multipliez votre facteur par l`expression résultante pour arrondir. Dans le dernier problème, vous avez supprimé un 3 et vous obtenez  . Mais vous ne voulez pas vous débarrasser complètement des 3, il suffit de les prendre en compte pour simplifier les choses. Vous ne pouvez pas simplement supprimer des numéros sans les remettre! Multipliez le facteur par l`expression pour compléter cette section. Par exemple:
. Mais vous ne voulez pas vous débarrasser complètement des 3, il suffit de les prendre en compte pour simplifier les choses. Vous ne pouvez pas simplement supprimer des numéros sans les remettre! Multipliez le facteur par l`expression pour compléter cette section. Par exemple:
 . Mais vous ne voulez pas vous débarrasser complètement des 3, il suffit de les prendre en compte pour simplifier les choses. Vous ne pouvez pas simplement supprimer des numéros sans les remettre! Multipliez le facteur par l`expression pour compléter cette section. Par exemple:
. Mais vous ne voulez pas vous débarrasser complètement des 3, il suffit de les prendre en compte pour simplifier les choses. Vous ne pouvez pas simplement supprimer des numéros sans les remettre! Multipliez le facteur par l`expression pour compléter cette section. Par exemple:




6. Vérifiez votre travail en multipliant à l`équation d`origine. Si vous avez tout fait correctement, il est facile de vérifier si vous l`avez fait correctement. Multipliez votre facteur par les deux termes individuels entre parenthèses. S`il correspond au binôme original donné, alors vous l`avez bien fait. Du début à la fin, nous résolvons l`expression  à la pratique :
à la pratique :
 à la pratique :
à la pratique :




Partie 2 sur 3: Factoriser des binômes pour résoudre des équations

1. Facteur pour simplifier les équations afin qu`elles soient plus faciles à résoudre. Lors de la résolution d`une équation avec des binômes, en particulier des binômes complexes, il peut sembler qu`il n`y a aucun moyen de tout faire correspondre. Par exemple, essayez de résoudre les problèmes suivants :  . Une façon de le faire, en particulier avec les exposants, est de factoriser d`abord.
. Une façon de le faire, en particulier avec les exposants, est de factoriser d`abord.
 . Une façon de le faire, en particulier avec les exposants, est de factoriser d`abord.
. Une façon de le faire, en particulier avec les exposants, est de factoriser d`abord. - Devoir d`exercice :
- Rappelez-vous que les binômes ne peuvent avoir que deux termes. S`il y a plus de deux termes, vous devez apprendre à résoudre des polynômes.

2. Additionner et soustraire pour qu`un côté de l`équation soit égal à zéro. Toute cette stratégie repose sur l`un des faits les plus fondamentaux des mathématiques : quelque chose multiplié par zéro doit être égal à zéro. Donc, si votre équation est égale à zéro, alors l`un des termes factorisés doit être égal à zéro! Pour commencer, vous allez ajouter et soustraire pour qu`un côté soit égal à zéro.




3. Dissoudre la face non nulle comme vous en avez l`habitude. À ce stade, vous prétendez simplement que l`autre côté n`existe pas. Trouvez le plus grand diviseur commun, divisez-le, puis créez votre expression factorisée.




4. Mettre les termes à l`intérieur et à l`extérieur des parenthèses égaux à zéro. Dans le problème pratique, vous multipliez 2y par (4 – y), et cela doit être égal à zéro. Puisque quelque chose multiplié par zéro est égal à zéro, cela signifie que 2y ou (4 – y) doit être égal à zéro. Faites deux équations distinctes pour savoir quelle valeur y doit avoir pour que chaque côté soit égal à zéro.






5. Résoudre les deux équations pour zéro pour la ou les réponses finales. Vous pouvez obtenir une ou plusieurs réponses. N`oubliez pas qu`un seul côté doit être égal à zéro, vous pouvez donc obtenir quelques valeurs différentes pour y qui résolvent la même équation. Les dernières étapes de l`exercice :





6. Appliquez vos réponses à l`équation d`origine pour vous assurer qu`elles sont correctes. Une fois que vous avez trouvé les bonnes valeurs pour y, vous devriez pouvoir les utiliser pour résoudre l`équation. C`est aussi simple que d`essayer chaque valeur de y au lieu de la variable comme indiqué ci-dessous. Les réponses sont y = 0 et y = 4, donc :


 Cette réponse est correcte
Cette réponse est correcte

 Cette réponse est également correcte.
Cette réponse est également correcte.Partie 3 sur 3 : Traiter des problèmes plus difficiles

1. Rappelez-vous que les variables comptent comme des facteurs, même avec des exposants. Rappelez-vous que la factorisation consiste à déterminer quels nombres correspondent à l`entier. L`expression  est une autre façon de dire
est une autre façon de dire  . Cela signifie que vous pouvez placer n`importe quel x en dehors des parenthèses si l`autre terme en a un aussi. Traiter les variables comme des nombres normaux. Par exemple:
. Cela signifie que vous pouvez placer n`importe quel x en dehors des parenthèses si l`autre terme en a un aussi. Traiter les variables comme des nombres normaux. Par exemple:
 est une autre façon de dire
est une autre façon de dire  . Cela signifie que vous pouvez placer n`importe quel x en dehors des parenthèses si l`autre terme en a un aussi. Traiter les variables comme des nombres normaux. Par exemple:
. Cela signifie que vous pouvez placer n`importe quel x en dehors des parenthèses si l`autre terme en a un aussi. Traiter les variables comme des nombres normaux. Par exemple: peut être factorisé, car les deux termes contiennent un t. La réponse finale sera
- Vous pouvez même placer plusieurs variables en dehors des parenthèses en même temps. Par exemple, dans
les deux termes contiennent le même
. Vous pouvez le dissoudre dans

2. Reconnaître des binômes pas encore simplifiés en combinant des termes similaires. Prenons, par exemple, l`expression  . Ici, il semble que vous ayez affaire à quatre termes, mais si vous regardez de plus près, vous vous rendrez compte qu`il n`y en a que deux. Vous pouvez ajouter des termes similaires et puisque 6 et 14 n`ont pas de variable et que 2x et 3x partagent la même variable, ils peuvent être fusionnés. La dissolution est alors facile :
. Ici, il semble que vous ayez affaire à quatre termes, mais si vous regardez de plus près, vous vous rendrez compte qu`il n`y en a que deux. Vous pouvez ajouter des termes similaires et puisque 6 et 14 n`ont pas de variable et que 2x et 3x partagent la même variable, ils peuvent être fusionnés. La dissolution est alors facile :
 . Ici, il semble que vous ayez affaire à quatre termes, mais si vous regardez de plus près, vous vous rendrez compte qu`il n`y en a que deux. Vous pouvez ajouter des termes similaires et puisque 6 et 14 n`ont pas de variable et que 2x et 3x partagent la même variable, ils peuvent être fusionnés. La dissolution est alors facile :
. Ici, il semble que vous ayez affaire à quatre termes, mais si vous regardez de plus près, vous vous rendrez compte qu`il n`y en a que deux. Vous pouvez ajouter des termes similaires et puisque 6 et 14 n`ont pas de variable et que 2x et 3x partagent la même variable, ils peuvent être fusionnés. La dissolution est alors facile :





3. Reconnaître la "différence des carrés parfaits" spéciale. Un carré parfait est un nombre dont la racine est un nombre entier, tel que 
 ,
, 
 , ou même
, ou même 
 Si votre binôme est une somme négative avec deux carrés parfaits, comme
Si votre binôme est une somme négative avec deux carrés parfaits, comme  , alors vous pouvez simplement les utiliser dans cette formule:
, alors vous pouvez simplement les utiliser dans cette formule:

 ,
, 
 , ou même
, ou même 
 Si votre binôme est une somme négative avec deux carrés parfaits, comme
Si votre binôme est une somme négative avec deux carrés parfaits, comme  , alors vous pouvez simplement les utiliser dans cette formule:
, alors vous pouvez simplement les utiliser dans cette formule:





4. Apprenez à simplifier la « différence des cubes parfaits ». Comme les carrés parfaits, il s`agit d`une formule simple où deux cubes sont soustraits l`un de l`autre. Par exemple,  . Comme précédemment, trouvez la racine cubique de chacun et utilisez-la dans la formule :
. Comme précédemment, trouvez la racine cubique de chacun et utilisez-la dans la formule :
 . Comme précédemment, trouvez la racine cubique de chacun et utilisez-la dans la formule :
. Comme précédemment, trouvez la racine cubique de chacun et utilisez-la dans la formule :

![Binômes de factorisation {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Binômes de factorisation {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)


5. Sachez que la somme des cubes parfaits rentre aussi dans une formule. Contrairement à la différence des carrés parfaits, vous pouvez utiliser des cubes ajoutés, tels que  , aussi facile à trouver avec une formule simple. C`est presque exactement le même que ci-dessus, mais avec quelques avantages et inconvénients inversés. La formule est aussi simple que les deux autres, et il suffit de reconnaître les deux cubes du problème :
, aussi facile à trouver avec une formule simple. C`est presque exactement le même que ci-dessus, mais avec quelques avantages et inconvénients inversés. La formule est aussi simple que les deux autres, et il suffit de reconnaître les deux cubes du problème :
 , aussi facile à trouver avec une formule simple. C`est presque exactement le même que ci-dessus, mais avec quelques avantages et inconvénients inversés. La formule est aussi simple que les deux autres, et il suffit de reconnaître les deux cubes du problème :
, aussi facile à trouver avec une formule simple. C`est presque exactement le même que ci-dessus, mais avec quelques avantages et inconvénients inversés. La formule est aussi simple que les deux autres, et il suffit de reconnaître les deux cubes du problème :

![Binômes de factorisation {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Binômes de factorisation {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)

Des astuces
- Tous les binômes n`ont pas de diviseurs communs! Certains ont déjà été simplifiés au maximum.
- Si vous n`êtes pas sûr s`il existe un diviseur commun, divisez d`abord par des nombres plus petits. Par exemple, si vous ne voyez pas immédiatement que 16 est le diviseur commun de 32 et 16, commencez à diviser les deux nombres par 2. Cela laisse 16 et 8, qui peuvent aussi être divisés par 8. Maintenant vous avez 2 et 1, les plus petits facteurs. Il existe clairement un diviseur commun supérieur à 8 et 2.
- Notez qu`une sixième puissance (x) est à la fois un carré parfait et est un cube parfait. Vous pouvez donc appliquer l`une ou l`autre des formules spéciales ci-dessus, dans n`importe quel ordre, à un binôme qui est la différence des puissances sixièmes parfaites, telles que x - 64. Cependant, vous trouverez peut-être plus facile d`appliquer d`abord la formule de différence pour les carrés parfaits afin de pouvoir factoriser davantage le binôme.
Mises en garde
- Un binôme qui est la somme de carrés parfaits ne peut pas être factorisé.
Articles sur le sujet "Binômes de factorisation"
Оцените, пожалуйста статью
Similaire
Populaire