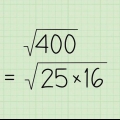Calculer la valeur absolue d'un nombre : 15 étapes (avec des images)

Teneur

Pas
- Méthode 1 sur 2 : Déterminer la valeur absolue
- Méthode 2 sur 2: Résolution d`équations complexes avec des valeurs absolues (équations avec `i`)
Des astuces

La valeur absolue d`un nombre est facile à trouver, et la théorie qui la sous-tend est importante pour résoudre des équations avec une valeur absolue. Chaque valeur absolue est une mesure de la distance entre ce nombre et zéro. Si vous pensez à une droite numérique, avec le zéro au milieu, vous pouvez savoir à quelle distance se trouve le nombre en question de ce zéro.

Pas

Méthode 1 sur 2 : Déterminer la valeur absolue

Image intitulée Trouver la valeur absolue d`un nombre Étape 1

1. Rappelez-vous que la valeur absolue est la distance d`un nombre à zéro. Une valeur absolue est la distance du nombre à zéro le long d`une droite numérique. Soit,

| - 4 |

${style d`affichage |-4|}$ indique donc simplement à quelle distance -4 est de zéro. Étant donné que la distance est toujours un numéro de position (vous ne pouvez pas vous déplacer par pas « négatifs », juste dans une direction différente), le résultat de la valeur absolue est toujours positif.

Image intitulée Trouver la valeur absolue d`un nombre Étape 2

2. Rendre le nombre dans les barres de valeur absolue positif. En termes simples, la valeur absolue rend tout nombre positif. Il est utile pour mesurer la distance ou déterminer des valeurs en matière financière, en travaillant avec des nombres négatifs tels que des dettes ou des prêts.

Image intitulée Trouver la valeur absolue d`un nombre Étape 3

3. Utilisez des barres verticales simples pour indiquer une valeur absolue. Le format pour une valeur absolue est facile. Lignes simples (trouvées près de la touche Entrée d`un clavier) autour d`un nombre ou d`une expression, telle que

| m |, | 3 + 5 |, | - 72 |

${style d`affichage |n|,|3+5|,|-72|}$ , indique une valeur absolue.

| 2 |

${style d`affichage |2|}$ est `la valeur absolue de 2.`

Image intitulée Trouver la valeur absolue d`un nombre Étape 4

4. Omettre les signes moins pour le nombre dans les marques de valeur absolue. Par exemple : |-5| devient alors |5|.

Image intitulée Trouver la valeur absolue d`un nombre Étape 5

5. Omettre les marques de valeur absolue. Le nombre qui reste est la réponse, donc |-5| devient |5| puis 5. Voici tout ce que vous devez faire :

| - 5 | = 5

${style d`affichage |-5|=5}$

Image intitulée Trouver la valeur absolue d`un nombre Étape 6

6. Simplifier l`expression dans la valeur absolue. Est-ce une expression simple, telle que

| - dix |

${style d`affichage |-10|}$ , alors vous pouvez simplement le rendre positif. Mais une expression comme

| (- 4 * 5) + 3 - 2 |

${style d`affichage |(-4*5)+3-2|}$ doit être simplifié avant de pouvoir trouver sa valeur absolue. L`ordre fixe des opérations s`applique toujours :

Mission:

| (- 4 * 5) + 3 - 2 |

${style d`affichage |(-4*5)+3-2|}$

Simplifiez entre parenthèses :

| (- 20) + 3 - 2 |

${style d`affichage |(-20)+3-2|}$

Additionner et soustraire :

| - 19 |

${style d`affichage |-19|}$

Faites en sorte que tout dans la valeur absolue soit positif :

| 19 |

${style d`affichage |19|}$

Réponse finale : 19

Image intitulée Trouver la valeur absolue d`un nombre Étape 7

sept. Utilisez toujours cet ordre d`opérations avant de calculer la valeur absolue. Lorsque vous travaillez sur des équations plus longues, vous effectuez tout le travail requis avant de déterminer la valeur absolue. N`essayez pas de simplifier les valeurs absolues jusqu`à ce que tout soit ajouté, soustrait et divisé correctement. Par exemple:

Mission:

1 + 2 + | 4 - sept | 5 * | - 3 * 2 |

${style d`affichage {frac {1+2+|4-7|}{5*|-3*2|}}}$

Faites l`ordre des opérations à l`intérieur et à l`extérieur de la valeur absolue :

3 + | - 3 | 5 * | - 6 |

${style d`affichage {frac {3+|-3|}{5*|-6|}}}$

Déterminer les valeurs absolues :

3 + (3) 5 * (6)

${style d`affichage {frac {3+(3)}{5*(6)}}}$

Ordre des opérations:

\frac{6}{30}

${style d`affichage {frac {6}{30}}}$

Simplifiez la réponse finale : $\frac{1}{5}$ ${frac{1}{5}}$

Image intitulée Trouver la valeur absolue d`un nombre Étape 8

8. Continuez à travailler sur quelques exemples d`exercices pour vous y habituer. Calculer la valeur absolue d`un nombre est très simple, mais cela ne veut pas dire que faire des exercices pratiques ne serait pas utile pour parfaire vos connaissances :

| 12 |

${style d`affichage |12|}$ =

12

${style d`affichage 12}$

| - 24 |

${style d`affichage |-24|}$ =

24

${style d`affichage 24}$

| 3 + 2 - 11 + 5 - 6 |

${style d`affichage |3+2-11+5-6|}$ =

sept

$sept$

Méthode 2 sur 2: Résolution d`équations complexes avec des valeurs absolues (équations avec `i`)

Image intitulée Trouver la valeur absolue d`un nombre Étape 9

1. Soyez prudent lorsque vous traitez des équations complexes impliquant des nombres imaginaires, tels que « i » ou -1{displaystyle {sqrt {-1}}} ${displaystyle {sqrt {-1}}}$ , et les résoudre séparément. Vous ne pouvez pas trouver la valeur absolue des nombres imaginaires de la même manière que vous pouvez trouver des nombres rationnels. Vous pouvez trouver la valeur absolue d`une équation complexe en la calculant dans la formule de distance. Prends l`expression

| 3 - 4 je |

${style d`affichage |3-4i|}$ par exemple.

Mission: $| 3 - 4 je |$ ${style d`affichage |3-4i|}$
Faites attention: Si vous utilisez une expression comme $\sqrt{- 1}$ ${displaystyle {sqrt {-1}}}$ vous pouvez le remplacer par `i.` La racine carrée de -1 est un nombre imaginaire, je. $| je | = 1$ ${style d`affichage |i|=1}$

Image intitulée Trouver la valeur absolue d`un nombre Étape 10

2. Trouver les coefficients de l`équation complexe. Prenons 3-4i comme équation d`une droite. La valeur absolue est la distance à zéro, vous déterminez donc la distance à zéro pour le point (3, -4) sur cette ligne.Les coefficients sont simplement les deux nombres qui ne sont pas `i`. Bien que le nombre à côté du i soit généralement le deuxième nombre, cela n`a pas d`importance lors de la résolution. Exercez-vous avec les coefficients suivants :

| 1 + 6 je |

${style d`affichage |1+6i|}$ = (1, 6)

| 2 - je |

${style d`affichage |2-i|}$ = (2, -1)

| 6 je - 8 |

${style d`affichage |6i-8|}$ = (-8, 6)

Image intitulée Trouver la valeur absolue d`un nombre Étape 11

3. Supprimer les symboles de valeur absolue de l`équation. Vous n`avez plus besoin que des coefficients. Rappelez-vous que vous déterminez la distance de l`équation à partir de zéro. Étant donné que vous utiliserez la formule de distance à l`étape suivante, cela revient à déterminer la valeur absolue.

Image intitulée Trouver la valeur absolue d`un nombre Étape 12

4. Carré des deux coefficients. Pour déterminer la distance, vous utilisez la formule de distance, également appelée

\sqrt{X} 2 + {oui}^{2}

${displaystyle {sqrt {x^{2}+y^{2}}}}$ . Donc, dans un premier temps, vous devez mettre au carré les deux coefficients de l`équation complexe. On continue avec l`exemple :

| 3 - 4 je |

${style d`affichage |3-4i|}$ :

Coefficients : (3, -4)

Formule de distance :

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Carré des coefficients : `

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Faites attention: Répétez la formule de distance si vous ne la comprenez pas. Notez que la mise au carré des deux nombres les rend positifs, vous donnant essentiellement la valeur absolue.

Image intitulée Trouver la valeur absolue d`un nombre Étape 13

5. Placer le produit des nombres sous le radical. Le signe radical indique que vous soustrayez la racine carrée du nombre en dessous. Additionnez maintenant les nombres ensemble d`abord, sans rien faire sur le signe radical.

Coefficients : (3, -4)

Formule de distance :

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Carré des coefficients :

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Additionnez le produit des coefficients :

\sqrt{25}

${displaystyle {sqrt {25}}}$

Image intitulée Trouver la valeur absolue d`un nombre Étape 14

6. Prenez la racine carrée de votre réponse finale. Vous avez juste besoin de simplifier l`équation pour la réponse finale. Il s`agit de la distance entre votre « point » sur une droite numérique imaginaire et le point zéro. S`il n`y a pas de racine carrée, laissez simplement la réponse de la dernière étape sous le signe radical - c`est une réponse correcte.

Coefficients : (3, -4)

Formule de distance :

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Carré des coefficients :

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Additionnez le produit des coefficients :

\sqrt{25}

${displaystyle {sqrt {25}}}$

Soustrayez la racine carrée de la réponse finale : 5

$| 3 - 4 je | = 5$ ${style d`affichage |3-4i|=5}$

Image intitulée Trouver la valeur absolue d`un nombre Étape 15

sept. Essayez quelques exercices pratiques. Cliquez avec votre souris directement derrière les questions pour voir les réponses, en blanc.

| 1 + 6 je |

${style d`affichage |1+6i|}$ = 37

| 2 - je |

${style d`affichage |2-i|}$ = 5

| 6 je - 8 |

${style d`affichage |6i-8|}$ = 10

Des astuces

Si vous avez une variable dans une valeur absolue, vous ne pouvez pas supprimer les signes de valeur absolue à l`aide de cette méthode, car si la valeur de la variable est négative, la valeur absolue la rendrait positive.
Si vous avez une expression dans une valeur absolue, simplifiez l`expression avant de déterminer sa valeur absolue.
Lorsqu`un nombre positif se trouve dans les marqueurs de valeur absolue, la réponse est toujours ce nombre.
Vous avez besoin d`une méthode différente pour résoudre les équations de valeur absolue avec un x et un y, bien que la théorie derrière la valeur absolue soit utilisée comme base.
Une valeur absolue ne peut jamais être un nombre négatif, donc si vous voyez quelque chose comme | 2 - 4x| = -7, alors vous savez que cette équation est fausse sans avoir à la résoudre.