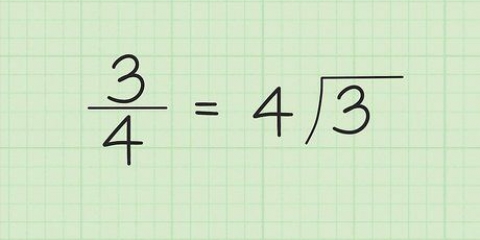Par exemple : l`inverse de 2 est 1 ÷ 2 = /2. 

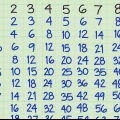
2/5 = 1 + 1 + /5 = /5 + /5 + /5 = /5 = /5. 
Dans l`exemple ci-dessus, /5 l`inverse de /14. 

Par exemple, l`inverse de 0,4 est 1 0,4. 
Par exemple, vous pouvez prendre 1 0,4 et le réécrire sous la forme 10 4. Dans ce cas, vous avez déplacé chaque décimale d`un espace vers la droite, ce qui revient à multiplier chaque nombre par dix. 
Trouver l'inverse d'un nombre
Teneur
L`inverse d`un nombre est utile dans toutes sortes d`équations algébriques. Par exemple, si vous divisez une fraction par une autre, vous multipliez essentiellement la première fraction par l`inverse de la seconde. Vous pouvez également avoir besoin de cette réciprocité pour trouver l`équation d`une ligne.
Pas
Méthode 1 sur 3: Trouver l`inverse d`une fraction ou d`un entier

1. Trouver l`inverse d`une fraction en l`inversant. La définition de « l`inverse » est simple. Pour trouver l`inverse de n`importe quel nombre, il suffit d`écrire ou de calculer `1 ÷ (ce nombre)`. Pour une fraction, l`inverse est juste une autre fraction, avec les nombres inversés, ou vice versa.
- L`inverse de /4 est donc /3.
- Le produit d`un nombre par sa réciproque est toujours égal à 1.

2. Écrire l`inverse d`un entier sous forme de fraction. Encore une fois, l`inverse d`un nombre est toujours 1 (ce nombre). Pour un nombre entier, écrivez cela sous forme de fraction - il ne sert à rien de le calculer à la virgule décimale.
Méthode 2 sur 3: Déterminer l`inverse d`un nombre composé

1. Reconnaître un nombre composé. Les nombres composés sont une combinaison d`un entier et d`une fraction, comme 2/5.Il y a deux étapes pour trouver l`inverse d`un nombre mixte expliqué ci-dessous.

2. Transformez-le en une fraction impropre. N`oubliez pas que le nombre 1 peut toujours être écrit sous la forme (nombre)/(même nombre), et que les fractions avec le même dénominateur (le nombre du bas) peuvent être additionnées. Voici un exemple avec 2/5:

3. Inverser la fraction. Une fois que le nombre est écrit complètement sous forme de fraction, vous pouvez trouver l`inverse comme vous le feriez avec n`importe quelle fraction, simplement en le retournant.
Méthode 3 sur 3: Déterminer l`inverse d`une décimale

1. Convertir un nombre décimal en fraction (si possible). Vous pouvez reconnaître certains nombres décimaux communs qui sont faciles peut s`écrire sous la forme d`une fraction.Par exemple : 0.5 = /2 et 0,25 = /4. Une fois sous forme de fraction, inversez la fraction pour vous retrouver avec l`inverse.
- Par exemple, l`inverse de 0,5 est /1 = 2.

2. Notez un problème de partage. Si vous ne pouvez pas le transformer en fraction, écrivez ou calculez l`inverse de ce nombre en tant que problème de division : 1 (le nombre décimal). Vous pouvez utiliser une calculatrice pour résoudre ce problème ou passer à l`étape suivante pour le résoudre à la main.

3. Changer le problème de division pour utiliser des nombres entiers. La première étape pour diviser des nombres décimaux déplace la virgule jusqu`à ce que tous les nombres soient des nombres entiers. Tant que vous déplacez la virgule pour les deux nombres du même nombre d`espaces, vous obtiendrez la bonne réponse.

4. Résoudre le problème en utilisant la division longue. Usage une longue division pour calculer l`inverse. Si vous calculez 10 4 avec cela, vous obtenez la réponse 2.5 (l`inverse de 0,4).
Des astuces
- L`inverse négatif d`un nombre est le même que l`inverse régulier multiplié par -1. La réciproque négative de /4 est -/3.
- Un inverse est parfois aussi appelé le inverse multiplicatif Nommé.
- Le nombre 1 est sa propre réciproque, puisque 1 1 = 1.
- Le nombre 0 n`a pas d`inverse, car 1 0 n`est pas défini.
Articles sur le sujet "Trouver l'inverse d'un nombre"
Оцените, пожалуйста статью
Similaire
Populaire