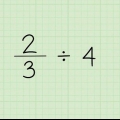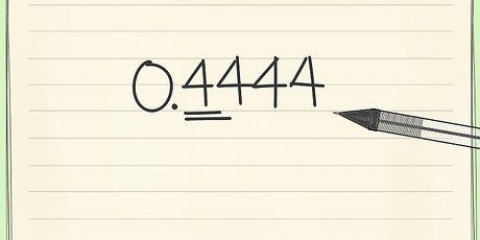Convertir une fraction en nombre décimal

Teneur

Pas
Des astuces

La conversion d`une fraction régulière en un nombre décimal est facile une fois que vous avez compris. Vous pouvez le faire simplement en effectuant une division longue, en multipliant ou en utilisant votre calculatrice si vous ne voulez pas le faire à la main. Une fois que vous aurez appris cette technique, vous pourrez convertir des fractions en nombres décimaux, et vice-versa avec facilité.

Pas

Méthode 1 sur 4: Utilisation de la division longue

$Image intitulée Changer une fraction commune en une étape décimale 1$

1. Écrivez le dénominateur en dehors des parenthèses autour de la division et le numérateur à l`intérieur. Supposons que vous travaillez avec le problème 3/4. Ensuite, écrivez un `4` à l`extérieur du signe de division et un `3` à l`intérieur. Le `4` est le diviseur et le `3` est le dividende.

$Image intitulée Changer une fraction commune en une étape décimale 2$

2. Placez un zéro suivi d`un point décimal au-dessus du signe de division. Puisque vous travaillez avec une fraction, vous savez que la réponse sera inférieure à un, donc la première étape est nécessaire. Après cela, mettez une décimale après le 3 sous le signe de division et mettez un zéro supplémentaire après. Bien que 3 et `3.0` soient identiques, le zéro après la virgule vous donne la possibilité de diviser 3,0 par 4.

$Image intitulée Changer une fraction commune en une étape décimale 3$

3. Utilisez la division longue pour obtenir la réponse. Quand tu fais une division longue, tu peux prétendre que la virgule n`existe pas et que tu divises juste 30 par 4. Vous procédez comme suit :

Divisez d`abord 3,0 par 4, ce qui peut être considéré comme 30. Le plus proche que vous pouvez obtenir est 4 x 7 = 28, avec un reste de 2. Donc, vous écririez 7 après le "0", au-dessus de la division et "28" en dessous du "3.0" en dessous de la division. Sous cela, écrivez 2, le reste, ou ce qui reste après avoir soustrait 28 de 30.

Ajoutez ensuite un autre « 0 » à « 3.0 » pour obtenir « 3.00 », ou tout ce que vous pourriez considérer comme « 300 » sous le signe de division. Cela vous permet de placer un autre 0 à côté du `2` afin que vous puissiez diviser 20 par 4.

Divisez 20 par 4 et vous obtenez « 5 » à droite de « 0,7 » au-dessus du signe de division, vous y écrivez donc « 0,75 ».

$Image intitulée Changer une fraction commune en une étape décimale 4$

4. Ecrivez votre réponse. Vous voyez que « 3 » divisé par « 4 » équivaut à « 0,75 ». Écrivez cette réponse et vous avez terminé.

Méthode 2 sur 4: Division d`une fraction avec une décimale répétée

$Image intitulée Changer une fraction commune en une étape décimale 5$

1. Écrire la division longue. Vous ne savez peut-être pas toujours que vous obtiendrez une réponse avec une décimale répétée lorsque vous commencez une division longue. Supposons que nous convertissions la fraction 1/3 en un nombre décimal. Écrivez le 3 (le dénominateur) à l`extérieur de la division et le 1 à l`intérieur de la division.

$Image intitulée Changer une fraction commune en une étape décimale 6$

2. Placez un zéro suivi d`une virgule, au-dessus du signe de division. Étant donné que votre réponse sera inférieure à un, il est utile d`écrire votre réponse sous forme de nombre décimal. Placez une virgule après le `1` à l`intérieur du caractère de division.

$Image intitulée Changer une fraction commune en une étape décimale 7$

3. Faire une longue division. Pour effectuer une division longue, commencez par faire du `1` un `1.0` afin de pouvoir diviser le nombre 10 par 3. Cela continue comme suit :

Divisez 10 par 3. Cela devient 3 x 3 = 9, reste 1. Vous écrivez donc un 3 après le "0", au-dessus du signe de division, et soustrayez la réponse, 9, de 10 pour obtenir le reste 1.

Ajoutez un autre « 0 » après le « 1 » sous le « 10 », pour obtenir à nouveau « 10 ». Lorsque vous divisez à nouveau 10 par 3, vous devrez répéter le processus, en plaçant un autre « 3 » après le premier « 3 » au-dessus de la marque de division, et en soustrayant un autre « 9 » du nouveau « 10 » qu’il vous reste.

Continuez jusqu`à ce que vous trouviez un modèle. Voyez-vous quelque chose de drôle? Vous remarquez que cela peut durer indéfiniment. Vous pouvez continuer à diviser 10 par 3, en laissant toujours 1 comme reste et en plaçant un autre « 3 » après la virgule décimale, au-dessus de la marque de division.

$Image intitulée Changer une fraction commune en une étape décimale 8$

4. Écrivez votre réponse. Maintenant que vous voyez le « 3 » se répéter, écrivez votre réponse sous la forme « 0,3 » avec une ligne au-dessus ou à travers le « 3 » pour indiquer que la virgule continue indéfiniment, ou sous la forme « 0,33 » avec un tiret au-dessus des deux nombres. C`est 1/3 sous forme décimale, car vous ne pourrez jamais obtenir une décimale finie parfaite comme réponse à cette fraction.

Il existe de nombreuses fractions avec des décimales répétées, telles que 2/9 (répétitions "0,2"), 5/6 ("0,83" avec répétitions "3") ou 7/9 (répétitions "0,7"). Cela se produit chaque fois que vous avez un dénominateur qui est un multiple de 3 qui ne rentre pas bien dans le numérateur.

Méthode 3 sur 4: Utilisation de la multiplication

$Image intitulée Changer une fraction commune en une étape décimale 9$

1. Recherchez un nombre que vous pouvez multiplier par le dénominateur de la fraction pour obtenir 10, 100, 1000 ou tout autre 1 suivi de zéros. Cela peut être un moyen facile de changer une fraction régulière en une fraction décimale sans utiliser votre calculatrice ou faire de longues divisions. Tout d`abord, vous devez trouver un moyen de multiplier le dénominateur de la fraction pour obtenir 10, 100, 1000, etc. pour obtenir. Vous pouvez trouver ce nombre en essayant de diviser le dénominateur par 10 d`abord, puis par 100, 1000, etc. jusqu`à ce que vous arriviez à un nombre entier. Voici quelques exemples:

3/5. 10/5 = 2, un entier. Vous pouvez multiplier cela par 5 x 2 = 10, donc 2 est le nombre que vous recherchez.
3/4. 10/4 = 2,5, ce qui n`est pas un entier, mais 100/4 = 25, et c`est un entier. Alors maintenant, vous savez que 4 x 25 = 100, donc 25 est le nombre que vous allez utiliser.
5/16. 10/16 = 0,625, 100/16 = 6,25, 1000/16 = 62,5, 10.000/16 = 625, qui est le premier entier. Alors maintenant, vous savez que 16 x 625 = 10.000, donc 625 est le nombre que vous recherchez.

$Image intitulée Changer une fraction commune en une étape décimale 10$

2. Multipliez le numérateur et le dénominateur de la fraction par ce nombre. Ce n`est pas si difficile. Multiplier le numérateur et le dénominateur de la fraction par le même nombre. Cela ressemblera à ceci :

3/5 x 2/2 = 6/10

3/4 x 25/25 = 75/100

5/16 x 625/625 = 3125/10.000

$Image intitulée Changer une fraction commune en une étape décimale 11$

3. Donnez votre réponse car le numérateur s`est déplacé vers la gauche de la virgule pour chaque 0 dans le numérateur. Ensuite, vérifiez le bas de votre dénominateur pour voir combien de zéros vous avez affaire. S`il n`y a pas plus d`un zéro, déplacez le point décimal d`une position vers la gauche, etc., et tu as ta réponse finale. Cela se passe comme ceci :

3/5 = 6/10 = 0,6

3/4 = 75/100 = 0,75

5/16 = 3125/10.000 = 0,3125

Méthode 4 sur 4: Utiliser une calculatrice

1. Diviser le numérateur par le dénominateur. C`est facile. Utilisez votre calculatrice pour diviser le numérateur par le dénominateur. Dans cet exemple : ¾ donc vous appuyez sur `3` suivi du symbole de division (`÷) suivi de 4 après quoi vous appuyez sur le signe est (`=`) et voyez votre réponse.

$Image intitulée Changer une fraction commune en une étape décimale 12$

$Image intitulée Changer une fraction commune en une étape décimale 13$

2. Écrivez votre réponse. Vous verrez que la réponse est 0,75. Par conséquent, la fraction 3/4 est égale à la virgule 0,75.

Des astuces

Pour vérifier votre réponse, multipliez-la par le dénominateur de la fraction originale ; le résultat devrait donner le numérateur de cette fraction.
Vous pouvez convertir certaines fractions en nombres décimaux en créant une fraction équivalente avec un dénominateur en base 10 (10, 100, 1000, etc.).) a. Ensuite, utilisez le système de valeur de position pour écrire la décimale correcte.