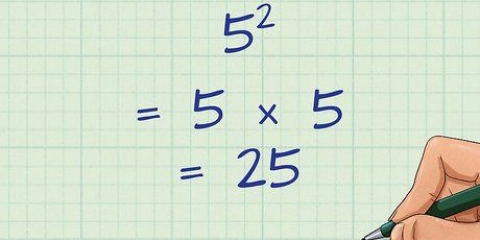Convertir des fractions en nombres décimaux

Teneur

Pas
Des astuces

Les fractions et les nombres décimaux appartiennent tous deux à l`ensemble des nombres rationnels. Convertir des fractions en nombres décimaux peut sembler déroutant au début, mais une fois que vous comprenez ce que sont réellement les fractions, cela devient beaucoup plus facile. Cet article explique d`abord ce qu`est une fraction puis les différentes manières de convertir une fraction en nombre décimal.

Pas

Méthode 1 sur 3: Comprendre les fractions

$Image intitulée Convertir des fractions en décimales Étape 1$

1. Essayez d`abord de comprendre ce qu`est une fraction normale. Une fraction se compose de trois parties : la compteur, le nombre au-dessus de la ligne de score, la ligne de score elle-même et le dénominateur, le nombre sous la ligne de fraction.

Le dénominateur indique combien de parties égales il y a dans un tout. Par exemple : une pizza peut être divisée en 8 morceaux. Le dénominateur de la pizza est alors `8`.
Le compteur indique le nombre à diviser. Une tranche de la pizza entière peut être représentée par un compteur de `1`. Divisez quatre par un « 4 » comme numérateur.
Dans cet exemple, vous avez mangé un morceau de pizza. Si vous avez mangé un morceau, il peut être représenté par 1/8, ou l`un des 8 morceaux. Si vous avez mangé trois morceaux, ce sera 3/8, etc.

$Image intitulée Convertir des fractions en décimales, étape 2$

2. Comprendre le nombre décimal. Un nombre décimal ou décimal, comme son nom l`indique, est basé sur le nombre 10, tout comme le système décimal. Les fractions décimales n`utilisent pas de ligne de rupture pour indiquer quelle partie du tout est signifiée. Au lieu de cela, le tout est basé sur 10, 100, 1000, etc. La fraction est représentée par les nombres à droite de la virgule décimale.

$Image intitulée Convertir les fractions en décimales Étape 3$

3. Comprenez que les deux performances sont en fait les mêmes. Les fractions et les décimales ne sont que des formes différentes d`une valeur inférieure à un nombre entier. Les différentes formes sont utilisées en fonction des différentes finalités que les gens ont pour les utiliser. Le poids et la taille sont souvent exprimés en fractions, mais les mesures scientifiques (nécessitant une plus grande précision) sont presque toujours exprimées en décimales. Le fait qu`ils puissent être utilisés de manière interchangeable signifie que vous devez souvent les convertir pour les ajouter, les soustraire ou les comparer.

Les décimales sont souvent lues d`une manière qui montre leur similitude avec la fraction ; Par exemple, 0,05 se prononce à voix haute comme "cinq centièmes", ce qui équivaut à 5/100.

Méthode 2 sur 3: Conversion d`une fraction à l`aide d`une division longue

$Image intitulée Convertir les fractions en décimales Étape 4$

1. Considérez une fraction comme une division. Le moyen le plus simple de convertir une fraction en nombre décimal est de lire la fraction comme une somme de division.

2/3, par exemple, peut également être considéré comme 2 sur 3 ; 5/8 est 5 divisé par 8 ; et 9/10 équivaut à 9 divisé par 10.
Une fraction est simplement le résultat d`une somme de division, quand ce qui reste n`est plus un nombre entier. Le numérateur (le haut de la fraction) devient le dividende, le dénominateur (le bas de la fraction) devient le diviseur, et la décimale que vous obtenez est le résultat.

$Image intitulée Convertir des fractions en décimales Étape 5$

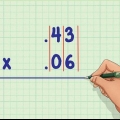
2. Considérez chaque chiffre comme faisant partie d`une colonne. Par exemple : le nombre 23,7 a un « 2 » dans la colonne des dizaines, un « 3 » dans la colonne des unités et après la virgule un « 7 » dans la dixième colonne (c`est-à-dire que le nombre est donc 7/10).

Si le dividende est inférieur au diviseur (ou en termes de fractions, si le numérateur est inférieur au dénominateur), alors le nombre avant la virgule est un 0.

Par exemple, si vous souhaitez convertir la fraction 3/4 le résultat devient inférieur à 1, vous obtenez donc un 0 dans la colonne des unités.

Idem après la virgule. Si le nombre dans la colonne des dixièmes (ou n`importe quelle colonne après) est inférieur au diviseur (encore une fois, le dénominateur dans la fraction), ajoutez un 0 au résultat et continuez à résoudre.

$Image intitulée Convertir les fractions en décimales Étape 6$

3. Ajouter un 0 à la fin du compteur. Dans la division longue, vous devez soustraire le diviseur du dividende, et cela n`est possible que si le dividende est supérieur au diviseur. Ajoutez ensuite un 0 à la fin du diviseur si vous avez un 0 après la virgule, cela n`a aucun effet sur le résultat.

Encore une fois, vous pouvez penser à la fraction 3/4 comme 3,0 4, donc vous l`écrivez de cette façon dans votre division longue.

$Image intitulée Convertir les fractions en décimales Étape 7$

4. Calculez combien de fois vous pouvez multiplier le diviseur pour vous rapprocher le plus possible du dividende.

Dans le cas de 3/4, vous traitez maintenant le 3 comme 30. 4 va 7 fois sur 30, et puis il te reste 2. Ainsi, le premier nombre de la colonne « dixièmes » devient 7, et vous ajoutez un autre « 0 » au reste de 2 afin que vous puissiez répéter le processus à nouveau. 4 entre exactement 5 fois dans 20, donc le résultat en décimal est de 0,75.

Méthode 3 sur 3: Conversion de fractions avec des puissances de 10 au dénominateur

$Image intitulée Convertir les fractions en décimales Étape 8$

1. Connaître les dénominateurs qui ont la puissance de 10 en eux. Un dénominateur "puissance de 10" est un dénominateur composé de n`importe quel exposant du nombre 10. Les nombres 1000 ou 1000000 sont des puissances de 10, mais dans la plupart des applications pratiques de cette méthode, vous aurez affaire aux nombres 10, 100 ou 1000.

$Image intitulée Convertir les fractions en décimales Étape 9$

2. Apprenez à reconnaître les fractions les plus faciles à convertir. Toute fraction avec un 5 comme dénominateur est un candidat clair, mais les fractions avec un dénominateur de 25 sont également très faciles à convertir.

$Image intitulée Convertir des fractions en décimales Étape 10$

3. Multiplier par 1. Comme vous le savez probablement, tous les nombres restent les mêmes lorsque vous les multipliez par 1. Mais vous pouvez aussi écrire 1 sous forme de fraction.

Par exemple, la fraction 2/2 est juste 1 (car 2 divisé par 2 égale 1). Pour convertir 1/5 en fraction avec le dénominateur 10, multiplier par 2/2. La réponse est alors 2/10.

Vous avez peut-être appris que vous devez simplifier les fractions autant que possible (surtout avec des nombres pairs). C`est juste le processus inverse, et cela ne change pas la valeur de la fraction.

$Image intitulée Convertir les fractions en décimales Étape 11$

4. Diviser le numérateur par le dénominateur. Vous n`avez pas besoin d`une longue division difficile pour cela. Tout ce que vous avez à faire est de traiter le numérateur comme le nombre entier, puis de reculer la virgule décimale d`une place en fonction du nombre de zéros dans le dénominateur.

Par exemple, vous avez la fraction 2/10. Le dénominateur a un 0. Donc, vous écrivez 2.0 pour cela (cela ne change pas la valeur), puis déplacez le point décimal d`une place vers la gauche. Vous obtiendrez alors `0.2` comme résultat.

Réessayez avec ce numéro : 28/1000. Le dénominateur a trois zéros. Nous écrivons maintenant `28` comme `28.0`. Maintenant, nous déplaçons la virgule décimale de trois positions vers la gauche, car le nombre a trois zéros. Le résultat est donc `0,028`.

Vous découvrirez bientôt que vous pouvez le faire avec toutes sortes de nombres qui ont un dénominateur facile (ou un dénominateur que vous pouvez facilement faire).

Des astuces

Un autre mot pour fraction est "fraction", qui vient du mot latin "frangere". Cela signifie « rupture » et c`est également la base de mots comme « fracture » et « fragment ».