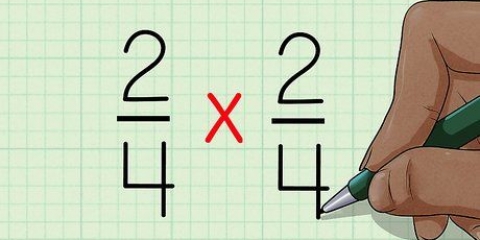(/2) = /2 × /2 ou (/2). La mise au carré de chaque nombre donne (/4). 
Le numérateur reste en haut de la fraction et le dénominateur reste en bas. Par exemple: (/2) = (/2x2) = (/4). 
Pour convertir cela en un nombre mixte, divisez 25 par 4. C`est 6 (6 x 4 = 24), avec un reste de 1. Par conséquent, le nombre mixte est 6/4. 

Par exemple: (-/4) = (–/4) X (-/4) 
Par exemple : (-2) x (-8) = (+16) 
En continuant avec l`exemple, la fraction résultante sera un nombre positif. (–/4) X (-/4) = (+/16) La coutume est d`omettre le signe plus des nombres positifs. 
Par exemple: (/16) a un facteur commun de quatre. Divisez la fraction par 4 : 4/4 = 1, 16/4 = 4 Réécrivez la fraction simplifiée : (/4) 

Par exemple : 16 × (/16) Mettez les parenthèses au carré et éliminez le facteur commun de 16 : 16 * /16 * /16 Comme il s`agit ici d`un 16 en nombre entier et de deux fois un 16 au dénominateur, vous pouvez éliminer l`un d`entre eux. Réécrivez l`équation simplifiée : 12 × /16 simplifier /16 en divisant par 4 : /4 Multiplier : 12 × /4 = 36/4 Pièce : 36/4 = 9 
Par exemple : 16 * (/16) Réécrivez avec le numérateur et le dénominateur au carré : 16 * (/16) Soustraire l`exposant au dénominateur : 16 * /16 Imaginez les 16 premiers comme un exposant de 1:16. En utilisant les règles de soustraction des puissances/exposants, vous soustrayez les exposants les uns des autres. 16/16, donne 16 = 16 ou 1/16. Maintenant vous continuez avec /16 Réécrivez et simplifiez la fraction : /16 =* /4. Simplifier : 12 × /4 = 36/4 Pièce : 36/4 = 9
Fractions au carré
Teneur
La mise au carré des fractions est l`une des opérations les plus simples que vous puissiez effectuer sur les fractions. C`est très similaire à la mise au carré d`entiers en ce sens que vous pouvez simplement multiplier à la fois le numérateur et le dénominateur par eux-mêmes. Il existe des cas où la simplification de la fraction avant la mise au carré rend la procédure plus facile. Si vous n`avez pas encore appris cette compétence, cet article fournit un bref aperçu pour améliorer votre compréhension.
Pas
Partie 1 sur 3: Mettre au carré des fractions

1. Comprendre comment mettre des nombres entiers au carré. Quand tu vois un nombre élevé à la puissance 2, tu sais mettre le nombre au carré. C`est la même chose que de multiplier le nombre par lui-même. Par exemple:
- 5 = 5 × 5 = 25

2. Vous rendez-vous compte que la quadraturefractions fonctionne de la même manière. Pour mettre une fraction au carré, multipliez la fraction par elle-même. Une autre façon de penser est de multiplier le numérateur par lui-même et le dénominateur par lui-même. Par exemple:

3. Multiplier le numérateur par lui-même et le dénominateur par lui-même. L`ordre réel dans lequel vous multipliez ces nombres par eux-mêmes n`a pas d`importance, tant que vous mettez les deux nombres au carré. Pour simplifier les choses, commencez par le numérateur : multipliez-le simplement par lui-même. Puis multipliez le dénominateur par lui-même.

4.Simplifier la fraction pour conclure. Lorsqu`il s`agit de fractions, la dernière étape consiste toujours à simplifier la fraction dans sa forme la plus simple ou à convertir une fraction impropre en un nombre mixte. Notre exemple, /4 est une fraction impropre car le numérateur est supérieur au dénominateur.
Partie 2 sur 3: Mettre au carré des fractions avec des nombres négatifs

1. Recherchez un signe moins devant la fraction. Si vous avez affaire à une fraction négative, il y a un signe moins devant elle. Il est sage de toujours mettre des parenthèses autour d`un nombre négatif afin que vous sachiez que le signe moins fait référence au nombre et n`est pas destiné à être une somme négative.
- Par exemple: (-/4)

2. Multiplier la fraction par elle-même. Carré de la fraction comme vous le feriez normalement, en multipliant le numérateur par lui-même, puis en multipliant le dénominateur par lui-même. Vous pouvez aussi simplement multiplier la fraction par elle-même.

3. Comprendre que multiplier deux nombres négatifs ensemble donne un nombre positif. Lorsqu`un signe moins est présent, la fraction entière devient négative. Lorsque vous mettez la fraction au carré, vous multipliez deux nombres négatifs. Lorsque deux nombres négatifs sont multipliés ensemble, le produit est toujours positif.

4. Supprimer le signe moins après la mise au carré. Si vous avez mis la fraction au carré, vous avez multiplié deux nombres négatifs. Cela signifie que la fraction au carré est positive. N`oubliez pas d`omettre le signe moins dans la réponse finale.

5. Simplifier la fraction autant que possible. La dernière étape des calculs de fractions consiste à simplifier. Les fractions incorrectes doivent d`abord être simplifiées en nombres fractionnaires, puis simplifiées davantage.
Partie3 sur 3: Utilisation de simplifications et de correctifs rapides

1. Vérifiez si vous pouvez faire la fractionsimplifier avant de le carré. Il est généralement plus facile de simplifier les fractions avant de mettre au carré. N`oubliez pas que simplifier une fraction implique de la diviser par un facteur commun jusqu`à ce que 1 soit le seul nombre qui puisse être divisé à la fois par le numérateur et le dénominateur. Simplifier une fraction d`abord signifie que vous n`avez pas à la simplifier à nouveau à la fin, lorsque les nombres sont plus gros.
- Par exemple: (/16)
- 12 et 16 peuvent tous deux être divisés par 4. 12/4 = 3 et 16/4 = 4 ; ainsi tu peux/16 simplifier à /4.
- Vous pouvez maintenant faire la fraction /4 au carré.
- (/4) = /16, que tu ne peux plus simplifier.
- Pour prouver cela, nous élevons au carré la fraction d`origine sans simplifier :
- (/16) = (/16x16) = (/256)
- (/256) a un facteur commun de 16. Diviser à la fois le numérateur et le dénominateur par 16 simplifie la fraction en (/16), la même fraction que nous avons obtenue en simplifiant d`abord.

2. Apprenez quand ne pas simplifier une fraction. Êtes-vous confronté à des problèmes plus complexes équations, alors il peut être possible d`éliminer l`un des facteurs. Dans un tel cas il est donc plus commode d`attendre en simplifiant la fraction. L`ajout d`un facteur supplémentaire à l`exemple ci-dessus rend cela plus clair.

3. Comprendre comment faire cela rapidement avec leexposant. Une autre façon de résoudre le même problème est de d`abord simplifier l`exposant. Le résultat sera le même, obtenu uniquement par une voie différente.
Nécessités
- Du papier ou un ordinateur
- Crayon/stylo (si vous utilisez du papier)
Articles sur le sujet "Fractions au carré"
Оцените, пожалуйста статью
Populaire