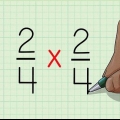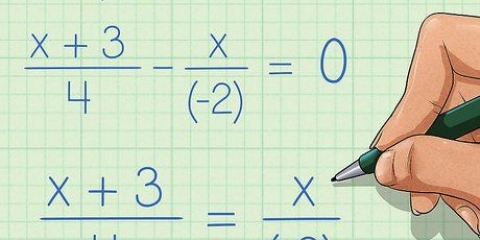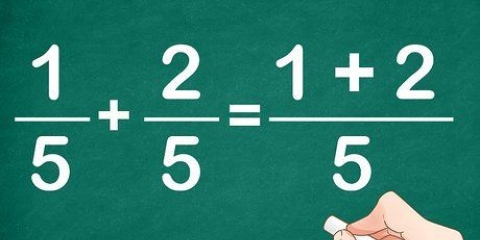Ajouter des fractions avec des dénominateurs différents : 9 étapes (avec photos)

Teneur

Pas
Des astuces

Avez-vous déjà eu des problèmes avec des problèmes mathématiques confus?? Une partie difficile des mathématiques pour de nombreuses personnes est de travailler avec des fractions, surtout lorsque vous commencez à additionner. Cela peut empirer une fois que les fractions ont des dénominateurs différents. Pourtant, c`est relativement facile, alors ne vous inquiétez pas. Suivez simplement les étapes ci-dessous.

Pas

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 1$

1. Écrivez les fractions. Placez-les côte à côte pour une bonne vue d`ensemble. Nous donnons des exemples ci-dessous pour chaque étape.

Ex. 1: 1/2 + 1/4

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 1Bullet1$

Ex. 2: 1/3 + 3/4

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 1Bullet2$

Ex. 3: 6/5 + 4/3

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 1Bullet3$

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 2$

2. Trouver le multiple commun des dénominateurs. Trouver un nombre divisible par les deux dénominateurs. Une façon directe de calculer ceci est de multiplier les deux dénominateurs ensemble.

Ex. 1: 2x4 = 8. les deux fractions obtiennent comme dénominateur 8.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 2Bullet1$

Ex. 2: 3x4 = 12. les deux fractions ont comme dénominateur 12.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 2Bullet2$

Ex. 3: 5x3 = 15. les deux fractions ont comme dénominateur 15.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 2Bullet3$

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 3$

3. Multipliez les deux nombres de premier fraction avec le dénominateur de la deuxième fraction. La valeur de la fraction ne change pas ; nous changeons simplement la façon dont la fraction "ressemble à".C`est toujours la même fraction.

Ex. 1: 1/2 x 4/4 = 4/8.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 3Bullet1$

Ex. 2: 1/3 x 4/4 = 4/12.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 3Bullet2$

Ex. 3: 6/5 x 3/3 = 18/15.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 3Bullet3$

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 4$

4. Multipliez les deux nombres de deuxième fraction avec le dénominateur de la première fraction. Encore une fois, nous ne modifions pas la valeur de la fraction ; nous changeons seulement la façon dont la fraction "ressemble à".C`est toujours la même fraction.

Ex. 1: 1/4 x 2/2 = 2/8.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 4Bullet1$

Ex. 2: 3/4 x 3/3 = 9/12.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 4Bullet2$

Ex. 3: 4/3 x 5/5 = 20/15.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 4Bullet3$

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 5$

5. Placez les deux fractions l`une à côté de l`autre avec les nouveaux nombres. Nous ne les avons pas encore additionnés, juste un peu de patience! Ce que nous avons fait est de multiplier chaque fraction par 1.

Ex. 1: au lieu de 1/2 + 1/4, nous avons 4/8 + 2/8

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 5Bullet1$

Ex. 2: au lieu de 1/3 + 3/4, nous avons 4/12 + 9/12

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 5Bullet2$

Ex. 3: au lieu de 6/5 + 4/3, nous avons 18/15 + 20/15

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 5Bullet3$

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 6$

6. Additionner les numérateurs des deux fractions ensemble. Le numérateur est le nombre supérieur de la fraction.

Ex. 1: 4 + 2 = 6. 6 sera notre compteur.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 6Bullet1$

Ex. 2: 4 + 9 = 13. 13 sera notre compteur.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 6Bullet2$

Ex. 3: 18 + 20 = 38. 38 sera notre compteur.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 6Bullet3$

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 7$

sept. Prenez le multiple que vous avez trouvé à l`étape 2 et placez-le sous votre nouveau comptoir.

Ex. 1: 8 sera notre nouveau dénominateur.

$Image intitulée Ajouter des fractions avec des dénominateurs différents Étape 7Bullet1$

Ex. 2: 12 sera notre nouveau dénominateur.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 7Bullet2$

Ex. 3: 15 sera notre nouveau dénominateur.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 7Bullet3$

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 8$

8. Placez le nouveau numérateur au-dessus de la ligne de score et le nouveau dénominateur en dessous de la ligne de score.

Ex. 1: 6/8 est notre réponse à 1/2 + 1/4 = ?

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 8Bullet1$

Ex. 2: 13/12 est notre réponse à 1/3 + 3/4 = ?

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 8Bullet2$

Ex. 3: 38/15 est notre réponse à 6/5 + 4/3 = ?

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 8Bullet3$

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 9$

9. Simplifier et extraire le nombre entier de la fraction. Simplifier la fraction en divisant à la fois le numérateur et le dénominateur par le plus grand diviseur commun.

Ex. 1: 6/8 peut être simplifié en 3/4.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 9Bullet1$

Ex. 2: 13/12 devient alors 1 1/12.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 9Bullet2$

Ex. 3: 38/15 devient alors 2 8/15.

$Image intitulée Ajouter des fractions avec des dénominateurs différents, étape 9Bullet3$

Des astuces

N`oubliez pas de simplifier.
N`oubliez pas de multiplier tous les nombres de la fraction par le même nombre.
Simplifiez toujours en dernier, les chiffres sont plus faciles à utiliser. À moins bien sûr qu`on ne vous demande de ne pas le faire.
Les dénominateurs doivent être les mêmes pour additionner des fractions, ils sont donc appelés "moyenne" dénominateurs. N`essayez pas de résoudre ce problème avant d`avoir effectué toutes les conversions - cela vous fera simplement plus de travail.