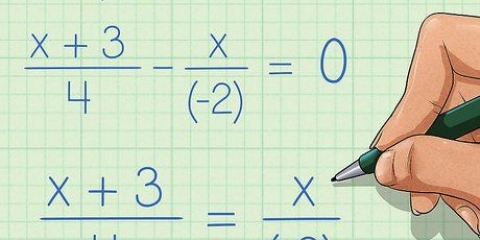18 ÷ 3 = 6, donc 2/3 = (2x6)/(3x6)=12/18 18 ÷ 6 = 3, donc 5/6 = (5x3)/(6x3)=15/18 18 ÷ 3 = 6, donc 1/3 = (1x6)/(3x6)=6/18 

6/18 = (6 6)/(18 6) = 1/3 12/18 = (12 6)/(18 6) = 2/3 15/18 = (15 3)/(18 3) = 5/6 La réponse est "1/3, 2/3, 5/6" 

C`est ce qu`on appelle la multiplication croisée, car vous multipliez des nombres ensemble en diagonale. 



N`oubliez pas de toujours placer le produit de la multiplication à côté de la fraction dont vous avez utilisé le numérateur. 
3/5=(3x3)/(5x3)=9/15 2/3=(2x5)/(3x5)=10/15 9/15 est inférieur à 10/15 Donc 3/5 est inférieur à 2/3 

8/3 = 2 + 2/3 9/9 = 1 19/4 = 4 + 3/4 13/6 = 2 + 1/6 
1 est le plus petit 2 + 2/3 et 2 + 1/6 (on ne sait pas encore lequel est plus gros que l`autre) 4 + 3/4 est le plus grand 
2/3 = (2x2)/(3x2) = 4/6 1/6 = 1/6 4/6 est supérieur à 1/6 2 + 4/6 est supérieur à 2 + 1/6 2 + 2/3 est supérieur à 2 + 1/6 

Trier les fractions par taille
Teneur
Bien qu`il soit facile d`ordonner des nombres entiers comme 1, 3 et 8 par taille, ce n`est pas toujours évident avec les fractions. Si chaque dénominateur est égal, vous pouvez les ordonner comme des entiers, par exemple. 1/5, 3/5 et 8/5. Dans d`autres cas, vous pouvez convertir les fractions pour qu`elles aient le même dénominateur, sans changer la valeur de la fraction. Cela devient plus facile avec la pratique et vous pouvez utiliser quelques astuces pratiques, à la fois pour comparer deux fractions ou pour commander des fractions où le numérateur est supérieur au dénominateur, les fractions impropres telles que 7/3.
Pas
Méthode 1 sur 3 : Commander un nombre quelconque de fractions

1. Trouver un dénominateur égal pour toutes les fractions. Utilisez l`une des méthodes suivantes pour trouver un dénominateur ou diminuez le nombre d`une fraction, que vous pouvez utiliser pour réécrire chaque fraction de la liste pour une comparaison facile. C`est ce que vous appelez un dénominateur commun, ou la le plus petit dénominateur commun si c`est le plus petit possible :
- Multipliez chaque dénominateur ensemble. Par exemple, si vous comparez 2/3, 5/6 et 1/3, multipliez ces dénominateurs ensemble : 3 x 6 = 18. C`est une méthode simple mais qui aboutit souvent à un nombre beaucoup plus important que les autres méthodes, qui sont un peu plus délicates.
- Ou lister les multiples de chaque dénominateur dans une colonne séparée, jusqu`à ce qu`un nombre qui se produit plus souvent ressorte. Par exemple, à 2/3, 5/6 et 1/3, vous avez des multiples de liste de 3:3, 6, 9, 12, 15, 18. Puis une liste de multiples de 6 : 6, 12, 18. Parce que 18 apparaît dans les deux listes, utilisez ce numéro (vous pouvez également utiliser 12, mais les exemples ci-dessous supposent que vous utilisez 18).

2. Convertissez chaque fraction pour qu`elles aient un dénominateur égal. N`oubliez pas que si vous multipliez le numérateur et le dénominateur d`une fraction par le même nombre, la valeur de la fraction reste la même. Utilisez cette technique avec chaque fraction, une à la fois, afin que chaque fraction ait le même dénominateur. Essayez ceci pour 2/3, 5/6 et 1/3, avec le dénominateur 18 :

3. Ordonner les fractions par les numérateurs. Maintenant que toutes les fractions ont le même dénominateur, elles sont faciles à comparer. Commandez-les du plus petit au plus grand selon le comptoir. Cela nous donne la liste suivante : 6/18, 12/18, 15/18.

4. Remettre chaque fraction à sa forme originale. Laissez les fractions dans cet ordre, mais reconvertissez-les dans la fraction d`origine. Pour ce faire, vous vous souvenez simplement de quelle fraction appartient à laquelle ou en divisant à nouveau les nombres supérieur et inférieur de la fraction :
Méthode 2 sur 3: Ordonner deux fractions avec multiplication croisée

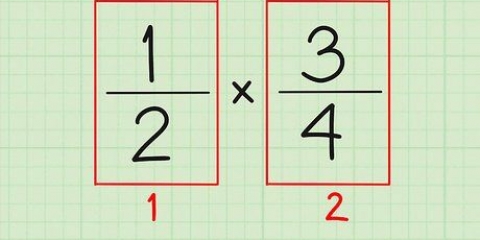
1. Écris les deux fractions côte à côte. Par exemple, comparez la fraction 3/5 et la fraction 2/3. Écrivez-les côte à côte : 3/5 à gauche et 2/3 à droite.

2. Multiplier le numérateur de la première fraction par le dénominateur de la seconde. Donc : 3 x 3 = 9.

3. Écrivez votre réponse à côté de la première fraction. Écrivez le produit de 3 x 3 = 9, à côté de la première fraction.

4. Multipliez le numérateur de deuxième fraction avec le dénominateur de la premier. Maintenant pour voir laquelle est la plus grande, nous comparons la réponse avec une autre multiplication. Multipliez ces deux nombres ensemble. Dans cet exemple (on compare 3/5 et 2/3), on multiplie 2 x 5.

5. Écrivez la réponse à côté de la deuxième fraction. Écrivez le résultat de 2 x 5 =10 à côté de la deuxième fraction.

6. Comparer les valeurs des résultats. Si une valeur est supérieure à l`autre, la fraction à côté du résultat est également la plus grande. Donc, puisque 9 est inférieur à 10, 3/5 est inférieur à 2/3.

sept. Comment ça marche exactement? Ce que vous faites est de convertir les fractions pour qu`elles aient toutes les deux le même dénominateur. C`est donc ce que fait réellement la multiplication croisée! Il saute en fait d`écrire les dénominateurs car en cas de dénominateurs similaires, vous n`avez qu`à comparer les numérateurs. Donc comme suit, sans la courte route de la multiplication croisée :
Méthode 3 sur 3: Ordre des fractions supérieures à un

1. Utilisez cette méthode pour les fractions où le numérateur est supérieur au dénominateur. Si le numérateur est supérieur au dénominateur, alors cette fraction est supérieure à 1. 8/3 en est un exemple. Vous pouvez également l`utiliser pour les fractions avec le même numérateur et dénominateur, comme 9/9. Ce sont deux exemples de "non conforme" fractions.
- Vous pouvez toujours utiliser les autres méthodes pour ces fractions. Cette méthode vous aidera à mieux comprendre ces fractions et peut être un peu plus rapide.

2. Convertir n`importe quelle fraction impropre en fraction mixte. Faites-en une combinaison d`un entier et d`une fraction. Parfois, vous pouvez facilement le faire par cœur. Par exemple, 9/9 = 1. Dans les cas les plus délicats, utilisez la division longue pour savoir combien de fois le dénominateur est divisible par le numérateur. Tout reste de la division longue reste comme une fraction. Par exemple:

3. Trier les nombres mixtes par le nombre entier. Maintenant qu`il n`y a plus de fractions impropres, vous avez une meilleure idée de la taille de chaque nombre. Ignorez d`abord les fractions et triez chaque nombre mixte par l`entier :

4. Comparez les fractions dans chaque groupe si nécessaire. Si vous avez plusieurs nombres mixtes avec le même nombre entier, comme 2 + 2/3 et 2 + 1/6, comparez la fraction des deux nombres pour savoir lequel est le plus grand. Dans l`exemple, nous comparons 2 + 2/3 et 2 + 1/6, en convertissant les fractions au même dénominateur :

5. Utilisez le résultat pour trier davantage la liste des nombres mixtes. L`ordre de toute la liste devient maintenant : 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.

6. Convertissez les nombres mixtes en fractions d`origine. Conservez le même ordre, mais annulez les modifications et réécrivez les fractions comme les fractions impropres d`origine : 9/9, 8/3, 13/6, 19/4.
Des astuces
- Lors du séquençage d`un grand nombre de fractions, il peut être utile de comparer de petits groupes de 2, 3 ou 4 fractions.
- Bien que trouver le plus petit dénominateur commun puisse être utile, tout dénominateur commun fonctionnera. Essayez de classer 2/3, 5/6 et 1/3 avec un dénominateur commun de 36 et voyez si vous obtenez le même résultat.
- Si les numérateurs sont tous les mêmes, vous pouvez également ordonner rapidement les fractions. Par exemple, 1/8 < 1/7 < 1/6 < 1/5. Pensez-y comme si c`était une pizza : si vous passez de 1/2 à 1/8, vous coupez la pizza en 8 morceaux au lieu de 2 et les morceaux sont plus petits.
Articles sur le sujet "Trier les fractions par taille"
Оцените, пожалуйста статью
Populaire