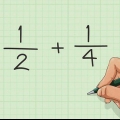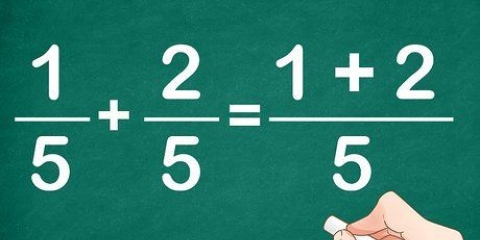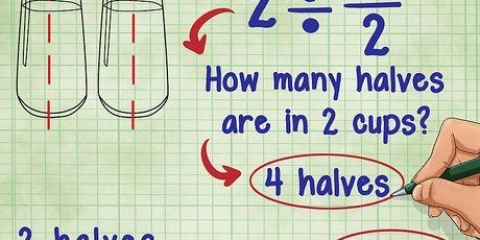Ex. 1: 1/4 + 2/4
Ex. 2: 3/8 + 2/8 + 4/8
Ex. 1: 1/4 + 2/4 est notre équation. "1" et"2" sont les compteurs. Cela signifie 1 + 2 = 3.
Ex. 2: 3/8 + 2/8 + 4/8 est notre équation. "3" et"2" et"4" sont les compteurs. Cela signifie 3 + 2 + 4 = 9.
Ex. 1: 3 est notre nouveau numérateur, et 4 est le `nouveau` dénominateur. Cela donne la réponse : 3/4. 1/4 + 2/4 = 3/4.
Ex. 2 : 9 est notre nouveau numérateur et 8 est le « nouveau » dénominateur. Cela donne la réponse : 9/8. 3/8 + 2/8 + 4/8 = 9/8.
Si le numérateur est supérieur au dénominateur, comme dans par exemple. 2, alors au moins un nombre entier peut être retiré de la fraction. Diviser le numérateur par le dénominateur. Si on divise 9 par 8, on obtient 1 entier et un reste de 1. Mettez le nombre entier avant la fraction et le reste comme numérateur de la nouvelle fraction, en gardant le même dénominateur.9/8 = 1 1/8.

Ex. 3: 1/3 + 3/5
Ex. 4: 2/7 + 2/14
Ex. 3: 3x5 = 15. Les deux fractions ont 8 comme dénominateur.
Ex. 4: 14 est un multiple de 7. Il suffit donc de multiplier 7 par 2 pour obtenir 14. Les deux fractions ont alors un dénominateur de 14.
Ex. 3: 1/3 x 5/5 = 5/15.
Ex. 4: Pour cette fraction, il suffit de multiplier la première fraction par 2, car de cette façon, nous pouvons obtenir le dénominateur commun.
2/7 x 2/2 = 4/14. Ex. 3: 3/5 x 3/3 = 9/15.
Ex. 4: La deuxième fraction n`a pas besoin d`être multipliée car les deux fractions ont déjà le même dénominateur. Ex. 3: au lieu de 1/3 + 3/5, nous avons 5/15 + 9/15
Ex. 4: au lieu de 2/7 + 2/14, nous avons 4/14 + 2/14
Ex. 3: 5 + 9 = 14. 14 sera le nouveau compteur.
Ex. 4: 4 + 2 = 6. 6 sera le nouveau compteur.
Ex. 3: 15 sera notre nouveau dénominateur.
Ex. 4: 14 sera notre nouveau dénominateur.
Ex. 3: 14/15 est notre nouvelle réponse à 1/3 + 3/5 = ?
Ex. 4: 6/14 est notre réponse à 2/7 + 2/14 = ?
Ex. 3: 14/15 ne peut pas être simplifié.
Ex. 4: 6/14 peut être réduit à 3/7 en divisant à la fois le numérateur et le dénominateur par 2, le plus grand diviseur commun.
Additionner des fractions ensemble
Teneur
Être capable d`ajouter des fractions est une compétence très utile. Pas seulement pour l`école primaire et secondaire, c`est juste une compétence très pratique. En savoir plus sur l`ajout de fractions ici. Vous serez étonné de ce que vous pouvez apprendre en quelques minutes.
Pas
Méthode 1 sur 2: Première partie: Ajouter des fractions avec le même dénominateur

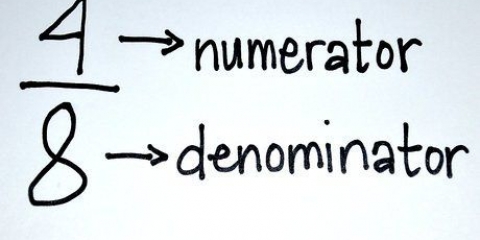
1. Vérifiez les dénominateurs (les nombres sous la ligne) de chaque fraction. S`ils ont le même nombre, alors vous avez affaire à des fractions avec des dénominateurs similaires. Sinon, sautez la section suivante.
2. Voici deux exemples de problèmes sur lesquels nous allons travailler dans cette section. Au moment où vous arrivez à la dernière étape, vous devriez comprendre comment fonctionne l`addition.


3. Prenez les deux numérateurs (les nombres au-dessus de la ligne) et additionnez-les. Peu importe le nombre de fractions que vous avez, si elles ont le même dénominateur, vous pouvez simplement additionner tous les numérateurs ensemble.


4. Construire la nouvelle fraction. Prenez la somme des numérateurs que vous avez obtenus à l`étape 2 ; cette somme devient le nouveau compteur. Utiliser le dénominateur des fractions de l`étape précédente. Ce sera le nouveau dénominateur; ce dénominateur reste toujours le même lorsque vous additionnez des fractions avec le même dénominateur


5. Simplifie si tu peux. Simplifiez la nouvelle fraction pour vous assurer que les nombres sont aussi petits que possible.

Méthode 2 sur 2: Deuxième partie: Ajouter des fractions avec des dénominateurs inégaux

1. Vérifiez les dénominateurs (chiffres sous la ligne de fraction) de chaque fraction. Si les dénominateurs sont inégaux, vous devez trouver un moyen de les rendre égaux. Lisez la suite pour savoir comment.
2. Voici deux exemples de problèmes sur lesquels nous allons travailler dans cette section. Lorsque nous arrivons à la dernière étape, vous savez comment additionner des fractions avec des dénominateurs différents.


3. Trouver un dénominateur approprié. Vous pouvez le faire en cherchant le multiple commun des dénominateurs. Un moyen facile de le trouver est de multiplier simplement les deux dénominateurs. Si l`un des dénominateurs est un multiple de l`autre, il vous suffit de multiplier cette autre fraction.


4. Multiplier les deux nombres de la première fraction par le dénominateur de la deuxième fraction. Il n`y a aucun changement dans la valeur de la fraction; nous changeons simplement à quoi ressemble la fraction. C`est toujours la même fraction.


5. Multiplier les deux nombres de la deuxième fraction par le dénominateur de la première fraction. Encore une fois, nous ne changeons pas la valeur de la fraction, seulement à quoi elle ressemble. C`est toujours la même fraction.

6. Placer les deux fractions l`une à côté de l`autre avec leurs nouveaux nombres. Ils n`ont pas encore été additionnés, juste un peu de patience! Ce que nous avons fait, c`est multiplier chaque fraction par un nombre approprié, dans le but de rendre les deux dénominateurs égaux.


sept. Additionner les numérateurs des deux fractions ensemble.


8. Prenez le dénominateur égal que vous avez calculé à l`étape 2 et utilisez-le comme dénominateur de la nouvelle fraction. Soit dit en passant, c`est bien sûr le même dénominateur que vous voyez déjà dans la fraction modifiée.




9. Simplifier la fraction. Simplifier la fraction en divisant à la fois le numérateur et le dénominateur par le plus grand diviseur commun.


Des astuces
Articles sur le sujet "Additionner des fractions ensemble"
Оцените, пожалуйста статью
Populaire