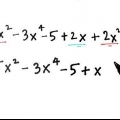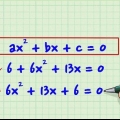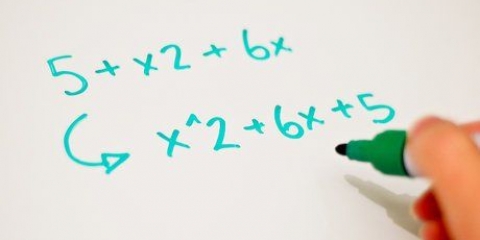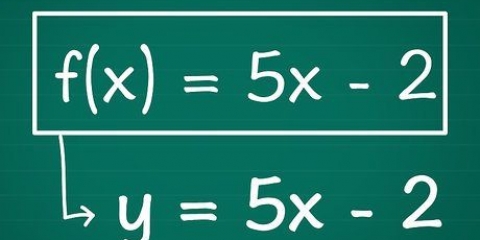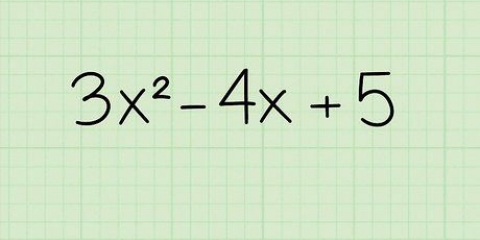Factorisation d'un polynôme du troisième degré : 12 étapes (avec des photos)

Teneur

Pas
- Partie 1 sur 2 : Dissoudre en regroupant
- Partie 2 sur 2: Affacturage avec le terme libre
Des astuces

Cet article concerne la factorisation d`un polynôme cubique, également appelé polynôme. Nous allons explorer comment nous pouvons le faire en utilisant le regroupement et en utilisant les facteurs du terme libre.

Pas

Partie 1 sur 2 : Dissoudre en regroupant

Image intitulée Factor a Cubic Polynomial Step 1

1. Diviser le polynôme en deux groupes. Diviser le polynôme aide à résoudre chaque partie individuelle.

Supposons que nous travaillons avec le polynôme suivant :" x + 3x - 6x - 18 = 0. Décomposons cela en (x + 3x) et (-6x - 18)

Image intitulée Factor a Cubic Polynomial Step 2

2. Essayez de découvrir ce qui est le même dans chaque groupe.

En (x + 3x), on voit que x est égal.

A (-6x - 18), on voit que -6 est égal.

Image intitulée Factor a Cubic Polynomial Step 3

3. Supprimer ces facteurs égaux des deux termes.

En factorisant x on obtient x(x + 3).

En décomposant -6 du deuxième morceau on obtient -6(x + 3).

Image intitulée Factor a Cubic Polynomial Step 4

4. Si chacun des deux termes contient le même facteur, alors vous pouvez combiner ces facteurs.

Cela donne (x + 3)(x - 6).

Image intitulée Factor a Cubic Polynomial Step 5

5. Trouvez la solution en regardant les racines. Si vous avez x dans une racine carrée, rappelez-vous que les nombres positifs et négatifs sont valables pour cette équation.

Les solutions sont -3, et √6.

Partie 2 sur 2: Affacturage avec le terme libre

Image intitulée Factor a Cubic Polynomial Step 6

1. Réorganisez l`expression sous la forme suivante : hache+bx+cx+d.

Supposons que vous travaillez avec l`équation : x - 4x - 7x + 10 = 0.

Image intitulée Factor a Cubic Polynomial Step 7

2. Trouver tous les facteurs de "ré". La constante "ré" devient le nombre sans variables à côté comme "X".

Les facteurs sont les nombres que vous pouvez multiplier ensemble pour obtenir un autre nombre. Dans ce cas, ce sont les facteurs de 10, ou "ré": 1, 2, 5 et 10.

Image intitulée Factor a Cubic Polynomial Step 8

3. Trouver un facteur qui rend le polynôme égal à zéro. Nous voulons déterminer quel facteur rend le polynôme égal à zéro si nous appliquons ce facteur pour "X" remplir l`équation.

Commencez par utiliser le premier facteur,1. remplacer "1" pour chaque "X" dans la comparaison :
(1) - 4(1) - 7(1) + 10 = 0

Cela donne : 1 - 4 - 7 + 10 = 0.

Puisque 0 = 0 est une affirmation vraie, vous savez que x = 1 est la solution.

Image intitulée Factor a Cubic Polynomial Step 9

4. Maintenant va tout réorganiser. Si x=1 alors il est possible d`écrire cette équation légèrement différemment sans changer le sens.

"x = 1" est le même que "x - 1 = 0" ou "(x - 1)". Tu n`en as qu`un "1" soustrait de chaque côté de l`équation.

Image intitulée Factor a Cubic Polynomial Step 10

5. Factoriser la racine carrée de l`équation. "(x - 1)" est la racine. Essayez de les prendre en compte dans le reste de l`équation. Faites cela avec un polynôme à la fois.

Pouvez-vous factoriser (x - 1) à partir de x? Non ce n`est pas possible. Mais si vous empruntez d`abord un -x à la deuxième variable : x(x - 1) = x - x.

Pouvez-vous factoriser (x - 1) à partir de ce qui reste de la deuxième variable? Non, ce n`est pas possible ici non plus. Vous devez à nouveau emprunter quelque chose à la troisième variable, qui est 3x de -7x. Cela nous donne -3x(x - 1) = -3x + 3x.

Puisque vous avez pris 3x sur -7x, la troisième variable est maintenant -10x et la constante est 10. Pouvez-vous délier cela. Oui bien sûr! -10(x - 1) = -10x + 10.

Ce que vous avez fait est de réorganiser les variables afin que vous puissiez obtenir le facteur (x - 1) de toute l`équation. L`équation modifiée ressemble à ceci : x - x - 3x + 3x - 10x + 10 = 0, mais est toujours la même que x - 4x - 7x + 10 = 0.

Image intitulée Factor a Cubic Polynomial Step 11

6. Procéder au remplacement des facteurs du terme libre. Regardez les nombres que vous avez résolus en utilisant (x - 1) à l`étape 5 :

x(x - 1) - 3x(x - 1) - 10(x - 1) = 0. Vous pouvez les réorganiser pour faciliter la dissolution à nouveau : (x - 1)(x - 3x - 10) = 0.

Ici, vous essayez juste de factoriser (x - 3x - 10). Les facteurs deviennent alors (x + 2)(x - 5).

Image intitulée Factor a Cubic Polynomial Step 12

sept. Votre solution est les racines factorisées. Vérifiez cette solution en insérant chacun d`eux dans l`équation d`origine.

(x - 1)(x + 2)(x - 5) = 0 Cela donne les solutions pour 1, -2 et 5.

Insérez -2 dans l`équation : (-2) - 4(-2) - 7(-2) + 10 = -8 - 16 + 14 + 10 = 0.

Insérez 5 dans l`équation : (5) - 4(5) - 7(5) + 10 = 125 - 100 - 35 + 10 = 0.

Des astuces

L`équation cubique est le produit de 3 équations du premier degré ou d`une équation du premier degré et d`une équation du deuxième degré qui ne peut pas être factorisée. Dans ce dernier cas, après avoir trouvé le polynôme du premier degré, vous utilisez une division longue pour trouver le polynôme du deuxième degré.
Il n`y a pas de polynômes cubiques qui ne peuvent pas être factorisés lorsqu`il s`agit de nombres réels, car cette équation doit avoir une racine carrée de nombres réels. Les équations du troisième degré telles que x + x + 1 qui ont une racine réelle irrationnelle ne peuvent pas être factorisées en polynômes avec des nombres entiers ou rationnels comme coefficient. Bien qu`il puisse être pris en compte dans l`équation elle-même, il ne peut pas être réduit à un polynôme entier.

La méthode 2 équivaut à une longue division de deux polynômes , un.v :

(x-1) ∕x³ - 4x²-7x+10 ∕

- 10x + 10................= (x-1) (-10)

Les déterministes x², -3x et -10 du quotient s`obtiennent en soustrayant toujours le 1er terme du diviseur ( x ) au premier terme du dividende, ou ce qu`il en reste ( x³, -3x², -10x ).