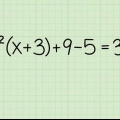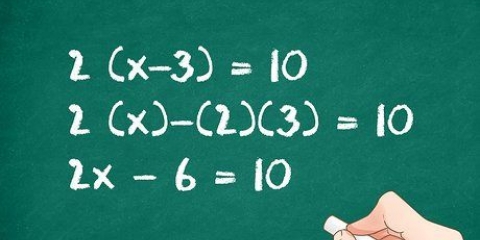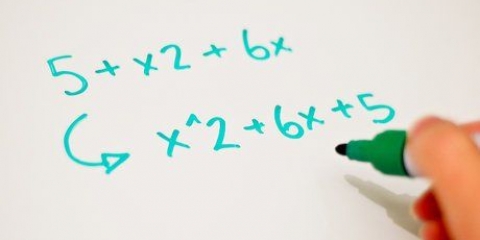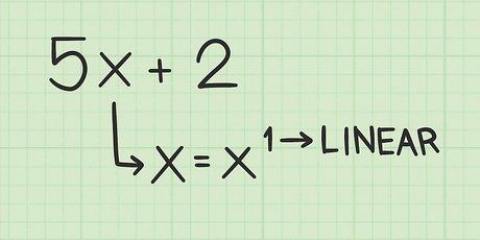3(x - 2/3) =
3(x - 2/3)(x -2/3) = 3[(x -2/3x -2/3x + 4/9)] 3(x - 4/3x + 4/9) 
-4/3 + 15/3 = 11/3.










Place de split
Teneur
La quadrature est une technique utile pour réécrire une équation quadratique, ce qui la rend plus facile à surveiller et à résoudre. Vous pouvez réécrire un carré en le réorganisant en morceaux plus faciles à gérer.
Pas
Méthode 1 sur 2 : Première partie : Réécrire une équation standard

1. Écrire l`équation. Supposons que vous vouliez résoudre l`équation suivante : 3x - 4x + 5.

2. Supprimer le coefficient de l`équation. Placer les 3 crochets extérieurs et diviser chaque terme sauf la constante par 3. 3x divisé par 3 est x et 4x divisé par 3 est 4/3x. Donc la nouvelle équation ressemble à ceci : 3(x - 4/3x) + 5. Le 5 est en dehors des crochets car vous ne l`avez pas divisé par 3.

3. Divisez le deuxième terme par 2 et carré. Le deuxième terme, également appelé b-terme dans l`équation, est 4/3. Réduire de moitié le deuxième mandat. 4/3 2, ou 4/3 x 1/2, équivaut à 2/3. Carré ce terme en multipliant à la fois le numérateur et le dénominateur par eux-mêmes. (2/3) = 4/9. Écrivez ce terme.

4. Addition et soustraction. Tu as ça"Additionnel" terme nécessaire pour convertir les trois premiers termes de l`équation en un carré. Mais rappelez-vous que vous avez ajouté ce terme en le soustrayant également de l`équation. Bien sûr, cela fait peu de différence de simplement combiner à nouveau les termes - alors vous serez de retour là où vous avez commencé. La nouvelle équation devrait maintenant ressembler à ceci : 3( x - 4/3 x + 4/9 - 4/9) + 5.

5. Obtenez le terme que vous avez soustrait en dehors des parenthèses. Parce que vous travaillez déjà avec les 3 en dehors des parenthèses, il n`est pas possible de simplement mettre -4/9 en dehors des parenthèses. Il faut d`abord le multiplier par 3. -4/9 x 3 = -12/9, ou -4/3. Si vous avez affaire à une équation qui ne contient qu`un coefficient 1 dex, vous pouvez sauter cette étape.

6. Convertir les termes entre parenthèses en carré. Votre équation ressemble maintenant à ceci : 3(x -4/3x +4/9). Vous avez travaillé d`avant en arrière pour obtenir 4/9, ce qui est en fait une autre façon de trouver le facteur qui complète le carré. Vous pouvez donc réécrire ces termes sous la forme : 3(x - 2/3). Vous pouvez vérifier cela en multipliant où vous verrez que vous obtenez à nouveau la même équation d`origine que la réponse.


sept. Fusionner les constantes. Vous avez maintenant deux constantes, 3(x - 2/3) - 4/3 + 5. Tout ce que vous avez à faire maintenant est d`ajouter -4/3 à 5 et cela donne 11/3 comme réponse. Pour ce faire, donnez-leur le même dénominateur : -4/3 et 15/3, puis ajoutez les deux numérateurs pour obtenir 11, en gardant le dénominateur égal à 3.


8. Écrire l`équation sous une autre forme. Maintenant tu as fini. L`équation finale est 3(x - 2/3) + 11/3. Vous pouvez éliminer le 3 en divisant l`équation par 3, vous laissant avec l`équation suivante : (x - 2/3) + 11/9.Vous avez maintenant écrit avec succès l`équation sous une autre forme : a( x - h ) + k, par lequel k la constante est.
Méthode 2 sur 2 : Deuxième partie : Résolution d`une équation quadratique

1. Notez la tâche. Supposons que vous vouliez résoudre l`équation suivante : 3x + 4x + 5 = 6

2. Additionnez les constantes et placez-les à gauche du signe égal. Les termes constants sont les termes sans variable. Dans ce cas vous en avez 5 à gauche et 6 à droite. Vous voulez déplacer 6 vers la gauche, alors soustrayez 6 des deux côtés de l`équation. Cela laisse 0 à droite (6-6) et -1 à gauche (5-6). L`équation ressemble maintenant à ceci : 3x + 4x - 1 = 0.

3. Prendre le coefficient du carré en dehors des parenthèses. Dans ce cas, 3 est le coefficient de x. Pour exclure 3 des parenthèses, supprimez le 3, placez le terme restant entre parenthèses et divisez chaque terme par 3. Donc, 3x 3 = x, 4x ÷ 3 = 4/3x et 1 ÷ 3 = 1/3. L`équation ressemble maintenant à ceci : 3(x + 4/3x - 1/3) = 0.

4. Divisez par la constante que vous venez de mettre entre crochets. Avec cela, vous vous débarrassez enfin de ces 3 ennuyeux en dehors des parenthèses. En divisant chaque terme par 3, il peut être éliminé sans changer l`équation. Vous avez maintenant : x + 4/3x - 1/3 = 0

5. Divisez le deuxième terme par 2 et carré. Prenons maintenant le deuxième terme, 4/3, de b terme, et diviser par 2. 4/3 2 ou 4/3 x 1/2, est 4/6, ou 2/3. Et 2/3 au carré c`est 4/9. Lorsque vous avez terminé, vous devez l`écrire à gauche et à droite de l`équation, car vous venez d`ajouter un nouveau terme. Vous devez le faire des deux côtés de l`équation. L`équation ressemble maintenant à ceci : x + 4/3 x + 2/3 - 1/3 = 2/3

6. Déplacez la constante d`origine vers la droite de l`équation et ajoutez-la au terme déjà présent. Déplacez la constante, -1/3, vers la droite pour en faire 1/3. Ajoutez ceci à l`autre terme, 4/9 ou 2/3. Trouver le plus petit commun multiple pour additionner 1/3 et 4/9. Cela donne ceci : 1/3 x 3/3 = 3/9. Ajoutez maintenant 3/9 à 4/9 pour avoir 7/9 du côté droit de l`équation. Cela donne : x + 4/3 x + 2/3 = 4/9 + 1/3 puis x + 4/3 x + 2/3 = 7/9.

sept. Écrivez le côté gauche de l`équation sous la forme d`un carré. Puisque vous avez déjà utilisé une formule pour trouver le terme manquant, le plus dur est déjà fait. Il suffit de mettre le x et la moitié du deuxième coefficient entre parenthèses et de le mettre au carré, comme ceci :(x + 2/3). Notez que la factorisation du carré donne 3 termes : x + 4/3 x + 4/9. L`équation ressemble maintenant à ceci : (x + 2/3) = 7/9.

8. Prendre la racine carrée des deux membres de l`équation. Du côté gauche de l`équation, la racine carrée de (x + 2/3) est égale à x + 2/3. Le côté droit donne +/- (√7)/3. La racine carrée du dénominateur 9 est 3, et la racine carrée de 7 est √7. N`oubliez pas d`écrire le +/- car la racine carrée d`un nombre peut être positive ou négative.

9. Mettre la variable de côté. Pour isoler la variable x du reste, déplacez la constante 2/3 vers la droite de l`équation. Vous avez maintenant deux réponses possibles pour x :+/- (√7)/3 - 2/3. Ce sont vos deux réponses. Vous pouvez le laisser ainsi ou élaborer sur la racine carrée, si on vous demande une réponse sans radical.
Des astuces
- Assurez-vous de mettre le +/- aux bons endroits sinon vous n`obtiendrez qu`une seule réponse.
- Même si vous connaissez la formule de la racine carrée, cela ne peut pas faire de mal de s`entraîner à diviser des carrés ou à élaborer des équations quadratiques de temps en temps. De cette façon, vous savez avec certitude que vous savez comment le faire quand c`est nécessaire.
Articles sur le sujet "Place de split"
Оцените, пожалуйста статью
Populaire