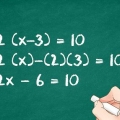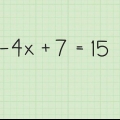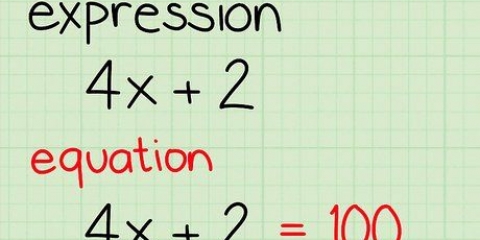4(x+3) + 9 - 5 = 32 
4x + 12 + 9 - 5 = 32 
4x+21-5 = 32 4x+16 = 32 4x + 16 - 16 = 32 - 16 4x = 16 
4x/4 = 16/4 x = 4 
2(x+3)+ 9 - 5 = 32 2(4+3)+ 9 - 5 = 32 2(7) + 9 - 5 = 32 4(7) + 9 - 5 = 32 28 + 9 - 5 = 32 37 - 5 = 32 32 = 32 

2x+12-12 = 44-12 2x = 32 
(2x)/2 = 32/2 x = 16 

2x + 12 = 44 2 x (4) + 12 = 44 2 x 16 + 12 = 44 32 + 12 = 44 44 = 44 

(x + 3)/6 = 2/3 6 x 2 = 12 (x + 3) x 3 = 3x + 9 3x + 9 = 12 
3x + 9 - 9 = 12 - 9 3x = 3 

(x + 3)/6 = 2/3 (1 + 3)/6 = 2/3 4/6 = 2/3 2/3 = 2/3 

(2x+9) - 5 + 5 = 0 + 5 (2x+9) = 5 
(√(2x+9)) = 5 2x + 9 = 25 
2x + 9 - 9 = 25 - 9 2x = 16 

(2x+9) - 5 = 0 (2(8)+9) - 5 = 0 (16+9) - 5 = 0 (25) - 5 = 0 5 - 5 = 0 

|4x +2| - 6 = 8 |4x +2| - 6 + 6 = 8 + 6 |4x +2| = 14 
4x + 2 = 14 4x + 2 - 2 = 14 -2 4x = 12 x = 3 
4x + 2 = -14 4x + 2 - 2 = -14 - 2 4x = -16 4x/4 = -16/4 x = -4 
(Pour x = 3) : |4x +2| - 6 = 8 |4(3) +2| - 6 = 8 |12 +2| - 6 = 8 |14| - 6 = 8 14 - 6 = 8 8 = 8 (pour x = -4) : |4x +2| - 6 = 8 |4(-4) +2| - 6 = 8 |-16 +2| - 6 = 8 |-14| - 6 = 8 14 - 6 = 8 8 = 8
Résoudre x dans une équation
Teneur
Il existe plusieurs façons de résoudre x dans une équation, que vous travailliez avec des exposants et des racines ou que vous ayez simplement besoin de diviser ou de multiplier. Quelle que soit la méthode que vous utilisez, vous devez toujours trouver un moyen d`isoler x d`un côté de l`équation afin de pouvoir calculer la valeur. Voici comment procéder :
Pas
Méthode 1 sur 5: Utilisation d`une équation linéaire ordinaire

1. Écrivez le problème. Voici le devoir :
- 2(x+3) + 9 - 5 = 32

2. Calculer l`exposant. Rappelez-vous l`ordre des opérations : HMVDOA, qui signifie Parenthèses, Exponentiation, Division/Multiply, Addition/Soustraction. Dans ce cas, vous ne pouvez pas d`abord déterminer ce qui est entre parenthèses car le x lui appartient, vous commencez donc par la puissance, 2. 2 = 4

3. Faire la multiplication. Multiplier 4 par (x+3). Voici comment:

4. Maintenant, travaillez l`addition et la soustraction. Il suffit d`ajouter ou de soustraire les nombres restants. Voici comment:

5. Isoler la variable. Pour ce faire, divisant les deux côtés de l`équation par 4 pour trouver x. 4x/4 = x et 16/4 = 4, donc x = 4.

6. Vérifiez votre calcul. Remplacez x = 4 dans l`équation d`origine pour vous assurer qu`elle est correcte. Voici comment:
Méthode 2 sur 5: Avec exponentiation

1. Écrivez le problème. Supposons que vous travaillez sur un problème où le terme x contient également un exposant :
- 2x + 12 = 44

2. Isoler le terme avec l`exposant. La première chose que vous devez faire maintenant est de combiner des termes similaires afin que toutes les constantes soient du côté droit de l`équation tandis que le terme avec l`exposant est à gauche. Il suffit de soustraire 12 des deux côtés. Voici comment:

3. Isoler la variable avec l`exposant, en divisant les deux côtés par le coefficient du terme x. Dans ce cas, 2 est le coefficient x, ce qui signifie que les deux côtés doivent être divisés par 2 afin de l`éliminer. Voici comment:

4. Prendre la racine carrée de chaque côté de l`équation. En calculant la racine carrée de x, il vous reste x à gauche et la racine carrée de 16,4, à droite. Donc, x = 4.

5. Vérifiez votre calcul. Remplacez x = 4 dans l`équation d`origine pour vous assurer qu`elle est correcte. Voici comment:
Méthode 3 sur 5: Utiliser des fractions

1. Écrivez le problème. Supposons que vous ayez affaire au problème suivant :
- (x + 3)/6 = 2/3

2. Multiplication croisée. Pour multiplier en croix, multipliez le dénominateur de chaque fraction par le numérateur de l`autre fraction. Alors, multipliez 6 (le premier dénominateur) par 2 (le deuxième numérateur), pour obtenir 12 du côté droit de l`équation.Multipliez ensuite 3 (le deuxième dénominateur) par x + 3 (le premier numérateur), pour obtenir 3 x + 9 à gauche de l`équation. Voici à quoi cela ressemblera :

3. Combiner des termes similaires. Combinez les constantes de l`équation en soustrayant 9 des deux côtés de l`équation. Voici ce qu`il faut faire :

4. Isoler x en divisant chaque terme par le coefficient x. Divisez simplement 3x et 9 par 3, le coefficient de x, et résolvez x. 3x/3 = x et 3/3 = 1, donc il vous reste x = 1.

5. Vérifiez votre calcul. Pour vérifier votre travail, remplacez x dans l`équation d`origine pour vous assurer qu`elle est correcte. Voici ce qu`il faut faire :
Méthode 4 sur 5: Utilisation des caractères racine

1. Écrivez le problème. Supposons que vous résolviez x dans le problème suivant :
- (2x+9) - 5 = 0

2. Isoler la racine carrée. Vous devez isoler la partie racine carrée de l`équation à gauche de l`équation avant de pouvoir continuer. Donc, vous ajoutez 5 aux deux côtés de l`équation. Voici comment:

3. Tracer la racine carrée des deux côtés. Tout comme vous divisez les deux côtés d`une équation par le coefficient multiplié par x, vous devez également prendre la racine carrée des deux côtés d`une équation si x est inférieur au signe radical. Cela supprime le radical de l`équation. Voici comment procéder :

4. Combiner des termes similaires. Combinez des termes égaux en soustrayant 9 des deux côtés de l`équation de sorte que toutes les constantes soient à droite, tandis que x reste à gauche. Voici ce qu`il faut faire :

5. Isoler la variable. La dernière chose à faire pour résoudre pour x est d`isoler la variable en divisant les deux côtés de l`équation par 2, le coefficient du terme x. 2x/2 = x et 16/2 = 8, il te reste donc x = 8.

6. Vérifiez votre calcul. Entrez à nouveau 8 dans l`équation pour x pour vérifier que votre calcul est correct :
Méthode 5 sur 5: Utiliser la valeur absolue

1. Écrivez le problème. Supposons que vous essayez de résoudre x dans le problème suivant :
- |4x +2| - 6 = 8

2. Isoler la valeur absolue. La première chose à faire est de combiner des termes similaires et d`isoler la valeur absolue. Dans ce cas, vous pouvez le faire en ajoutant 6 des deux côtés de l`équation. Voici comment:

3. Supprimer la valeur absolue et résoudre l`équation. C`est la première et la plus simple étape. Vous devez maintenant résoudre x deux fois, à chaque fois que vous travaillez avec une valeur absolue. Voici comment procéder la première fois :

4. Supprimez la valeur absolue et changez le signe des termes de l`autre côté du signe égal avant de continuer à résoudre. Maintenant, recommencez, cette fois en rendant la partie gauche de l`équation égale à -14 au lieu de 14. Voici comment:

5. Vérifiez votre calcul. Maintenant que vous savez que x = (3, -4), remplacez simplement les deux nombres dans l`équation pour vous assurer que c`est correct. Voici comment:
Des astuces
- Pour vérifier votre travail, entrez la valeur de x dans l`équation d`origine et résolvez-la.
- Les racines sont une autre façon de représenter les exposants.La racine carrée de x = x^1/2.
Articles sur le sujet "Résoudre x dans une équation"
Оцените, пожалуйста статью
Similaire
Populaire