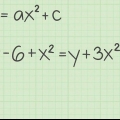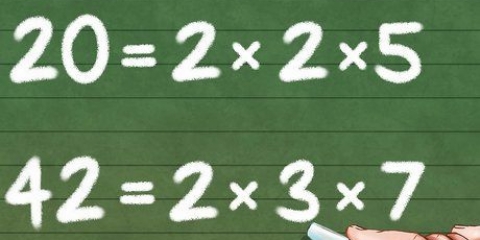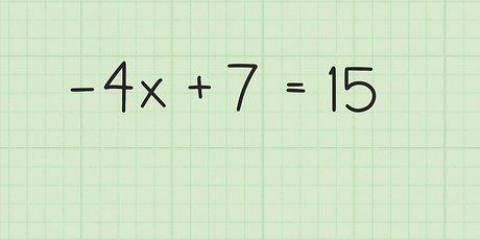Trouver la valeur extrême d'une équation : 10 étapes (avec des images)

Teneur

Pas
- Méthode 1 sur 2: La formule x = -b/2a
- Méthode 2 sur 2: Élaboration de l`équation
Des astuces
Mises en garde
Nécessités

La valeur extrême d`une parabole est le maximum ou le minimum de l`équation. Si vous voulez trouver la valeur extrême d`une équation quadratique, utilisez une formule ou résolvez l`équation. Ici, vous apprendrez comment faire cela.

Pas

Méthode 1 sur 2: La formule x = -b/2a

Image intitulée Trouver le sommet d`une équation quadratique Étape 1

1. Déterminer les valeurs de a, b et c. Dans une équation quadratique ou quadratique,X = une,X = b, et la constante (le terme sans variable) = c. Supposons que nous ayons affaire à l`équation suivante : oui = x + 9x + 18. Dans cet exemple, une = 1, b = 9 et c = 18.

Image intitulée Trouver le sommet d`une équation quadratique Étape 2

2. Utiliser une formule pour trouver la valeur de x. Le sommet de la parabole est aussi l`axe de symétrie de l`équation. La formule pour trouver la valeur extrême x d`une équation quadratique est x = -b/2a. Remplissez les valeurs pertinentes dans cette équation pour obtenir X trouver. Substituer les valeurs pour a et b. Voici comment:

x=-b/2a

x=-(9)/(2)(1)

x=-9/2

Image intitulée Trouver le sommet d`une équation quadratique Étape 3

3. Branchez la valeur de x dans l`équation d`origine pour obtenir la valeur de y. Maintenant que vous connaissez x, il est possible d`appliquer cette valeur à l`équation d`origine pour obtenir y. La formule pour déterminer la valeur extrême d`une équation quadratique est (x, y) = [(-b/2a), f(-b/2a)]. Cela signifie simplement que pour obtenir y, vous pouvez trouver x à l`aide de cette formule, puis le brancher dans l`équation d`origine. Voici comment ça se passe :

y = x + 9x + 18

y = (-9/2) + 9(-9/2) +18

y = 81/4 -81/2 + 18

y = 81/4 -162/4 + 72/4

y = (81 - 162 + 72)/4

y = -9/4

Image intitulée Trouver le sommet d`une équation quadratique Étape 4

4. Écrivez les valeurs de x et y sous la forme d`une paire ordonnée. Maintenant que vous savez que x = -9/2 et y = -9/4, écrivez simplement ces valeurs sous forme de paire ordonnée : (-9/2, -9/4). La valeur extrême de cette équation quadratique est (-9/2, -9/4). Si vous vouliez dessiner cette parabole dans un graphique, alors ce point est le minimum de la parabole, car x est positif.

Méthode 2 sur 2: Élaboration de l`équation

Image intitulée Trouver le sommet d`une équation quadratique Étape 5

1. Écrire l`équation. L`élaboration de l`équation est une autre façon de trouver la valeur extrême d`une équation quadratique. Avec cette méthode, il est possible de trouver les coordonnées x et y immédiatement. Disons que nous travaillons avec l`équation quadratique suivante : x + 4x + 1 = 0.

Image intitulée Trouver le sommet d`une équation quadratique Étape 6

2. Divisez chaque terme par le coefficient de x . Dans ce cas, le coefficient dex est égal à 1, vous pouvez donc sauter cette étape. Diviser chaque terme par 1 n`a pas d`importance!

Image intitulée Trouver le sommet d`une équation quadratique Étape 7

3. Déplacer la constante vers le côté droit de l`équation. La constante est le terme sans coefficient. Dans ce cas c`est "1". Déplacez le 1 de l`autre côté de l`équation en soustrayant 1 des deux côtés. Voici comment procéder :

x + 4x + 1 = 0

x + 4x + 1 -1 = 0 - 1

x + 4x = - 1

Image intitulée Trouver le sommet d`une équation quadratique Étape 8

4. Complétez le carré à gauche de l`équation.Travail (b/2) et ajouter le résultat des deux côtés de l`équation. remplir "4" en valeur de b, parce que "4x" le b-terme est de l`équation.

(4/2) = 2 = 4. Ajoutez maintenant 4 des deux côtés de l`équation pour obtenir ce qui suit :

x + 4x + 4 = -1 + 4

x + 4x + 4 = 3

Image intitulée Trouver le sommet d`une équation quadratique Étape 9

5. Factoriser le côté gauche de l`équation. Maintenant, vous verrez que x + 4x + 4 est un carré parfait. Cela peut être réécrit comme (x + 2) = 3

Image intitulée Trouver le sommet d`une équation quadratique Étape 10

6. Utilisez ceci pour trouver les coordonnées x et y. Vous pouvez trouver la coordonnée x en faisant simplement (x + 2) égal à zéro. Donc si (x + 2) = 0, alors que doit être x? La variable x devrait alors être égale à -2 pour compenser le +2, donc la coordonnée x est -2. La coordonnée y est simplement le terme constant de l`autre côté de l`équation. Donc, y = 3. Vous pouvez également prendre un raccourci et prendre le signe du nombre entre parenthèses pour trouver la coordonnée x. Donc, la valeur extrême de l`équation x + 4x + 1 = (-2, 3)

Des astuces

Comprendre ce que représentent a, b et c.
Montrez votre travail et vérifiez-le! En conséquence, votre professeur sait que vous comprenez et vous avez vous-même la chance de voir et de corriger les erreurs dans vos réponses.
Respecter cet ordre de traitement pour garantir un bon déroulement de la mission.