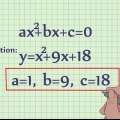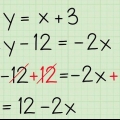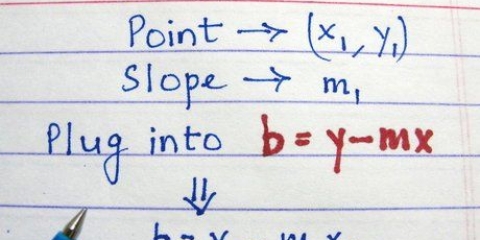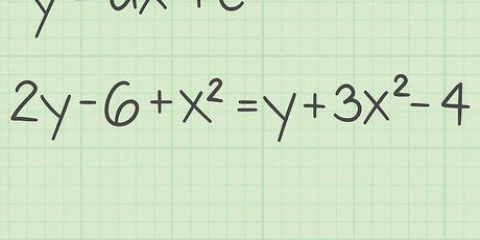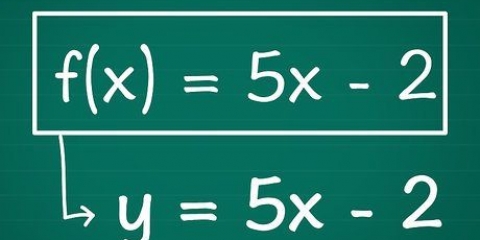Dans l`exemple d`équation ci-dessus, si vous divisez les deux côtés par 2, 2x = 6, vous obtenez 2/2 x = 6/2, ou x = 3. Ceci est l`ordonnée à l`origine de l`équation 2x + 3y = 6. Vous pouvez utiliser les mêmes étapes pour les équations de la forme ax^2 + by^2 = c. Dans ce cas, si vous entrez 0 pour y, vous obtenez x^2 = c/a, et après avoir trouvé la valeur à droite du signe égal, vous devez trouver la racine de x-carré. Cela vous donne 2 valeurs, 1 positive et 1 négative, qui totalisent 0. 

La factorisation consiste à diviser une équation quadratique en 2 expressions algébriques plus simples qui, lorsqu`elles sont multipliées ensemble, produisent l`équation quadratique. Souvent, les valeurs de a et c peuvent être la clé pour trouver les bons facteurs. Puisque 2 fois 5 égale 10, la valeur absolue de c, et parce que la valeur absolue de b est inférieure à celle de c, 2 et 5 sont probablement les composantes numériques des bons facteurs. Puisque 5 moins 2 est égal à 3, les facteurs corrects sont x + 5 et x - 2. Si vous remplissez les facteurs de l`équation quadratique, (x + 5)(x - 2) = 0, les 2x intersections sont -5 (-5 + 5 = 0) et 2 (2 - 2 = 0). Si vous utilisez la formule quadratique, insérez les valeurs pour a, b et c de la formule quadratique dans la formule (-b + ou - W (b^2 - 4 ac))/2a (où W est le carré root ) pour trouver la ou les valeurs de x. Si vous branchez les valeurs 1, 3 et -10 dans cette équation, vous obtenez (-3 + ou - W (3^2 - 4(1)(-10)))/2(1). La valeur à l`intérieur des parenthèses W sort à 9 -(-40) ou 9+40, qui est 49, donc l`équation sort à (-3 + ou - 7)/2, ce qui conduit à (-3 + 7 ) /2 ou 4/2, qui vaut 2, et (-3 -7)/2 ou -10/2, qui vaut -5. Contrairement aux simples équations à 2 variables décrites dans la section précédente, les équations quadratiques sur un graphique de coordonnées sont dessinées comme une parabole (une ligne courbe ressemblant à un "VOUS" ou "V") au lieu d`une ligne droite. Les équations quadratiques ne peuvent avoir aucune intersection x, 1 x intersection ou 2 x intersections.
Trouver l'intersection avec l'axe des x
Teneur
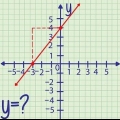
En algèbre, les graphiques bidimensionnels avec des coordonnées ont un axe horizontal, ou axe des x, et un axe vertical, ou axe des y. Les endroits où les lignes représentant une plage de valeurs coupent ces axes sont appelés intersections. L`ordonnée à l`origine est l`endroit où la ligne coupe l`axe des y, et l`intersection des x est l`endroit où la ligne coupe l`axe des x. Trouver l`abscisse à l`origine avec l`algèbre peut être simple ou compliqué, selon que l`équation n`a que 2 variables ou qu`elle est quadratique. Les étapes ci-dessous montrent comment cela fonctionne pour les deux types d`équations.
Pas
Méthode 1 sur 2 : Équations simples à 2 variables

1. Remplacez la valeur de y par 0. Au point où la ligne des valeurs croise l`axe horizontal, y a une valeur de 0.
- Dans l`exemple d`équation, si vous remplacez 2x + 3y = 6, y par 0, l`équation devient 2x + 3(0) = 6, donc en gros 2x = 6.

2. Trouver la solution pour x. Cela signifie généralement diviser les deux côtés de l`équation par le coefficient de x pour lui donner une valeur de 1.
Méthode 2 sur 2: Pour les équations quadratiques

1. Mettez l`équation sous la forme ax^2 + bx + c = 0. C`est la forme standard pour écrire une équation quadratique, où a est le coefficient de x au carré, b est le coefficient de x et c est une valeur purement numérique.
- Pour l`exemple de cette section, nous utiliserons l`équation x^2 +3x - 10 = 0.

2. Résoudre l`équation pour x. Il y a plusieurs façons de résoudre une équation quadratique. Les 2 dont nous traitons ici sont la factorisation et l`utilisation de la formule quadratique.
Des astuces
- Si dans l`exemple de comparaison ci-dessous "Équations simples à 2 variables" en entrant un 0 pour x au lieu de y, vous pouvez connaître la valeur de l`ordonnée à l`origine.
Articles sur le sujet "Trouver l'intersection avec l'axe des x"
Оцените, пожалуйста статью
Similaire
Populaire