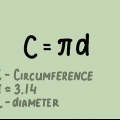Même le bouton d`une calculatrice n`utilise pas la valeur exacte de , bien qu`elle soit suffisamment précise. 
C est juste une façon plus courte d`écrire "circonférence". 
Vous avez peut-être écrit le côté gauche comme 2r, ce qui est aussi correct. Les gens aiment mettre les chiffres avant les symboles pour rendre l`équation plus facile à lire, mais cela ne change pas le résultat de l`équation. Dans une équation mathématique, vous pouvez toujours multiplier les côtés gauche et droit par la même quantité et toujours obtenir une équation correcte. 
Par exemple, si le rayon mesure deux unités de long, alors 2πr = 2 x (3,14) x (2 unités) = 12,56 unités = la circonférence. Dans le même exemple, mais en utilisant le bouton π d`une calculatrice pour une meilleure précision, vous obtenez 2 x π x 2 unités = 12,56637... unités, mais sauf indication contraire de votre professeur, vous pouvez arrondir le nombre à 12,57 unités. 

Nous utilisons ré`, ne pas2r, parce que ton problème de maths te dit quoi ré veux dire. Cependant, il est important de comprendre cette étape afin de ne pas vous tromper si votre professeur ou votre livre de mathématiques 2r utilisé là où vous avez un ré attendrait. 
Même le bouton d`une calculatrice n`utilise pas la valeur exacte de , bien qu`elle soit très précise. 

x d = (C / d) x d d = C 
Par exemple, si le diamètre est de six, vous obtenez (3,14) x (6) = 18,84. Dans le même exemple, mais en utilisant le bouton d`une calculatrice pour plus de précision, vous obtenez π x 6 = 18.84956... mais sauf indication contraire, vous pouvez arrondir le nombre à 18,85. 


A = r A / = r / π = r (A/π) = (r) = r r = (A/π) 
C = 2πr C = 2π(√(A/π)) 
La réponse pour cet exemple est 13.72937... mais sauf indication contraire, vous pouvez arrondir la réponse à 13.73. 


Assurez-vous d`enrouler la ficelle autour d`elle plus d`une fois. Vous devriez vous retrouver avec une seule boucle afin qu`il n`y ait aucune partie du cercle où la corde est enroulée en double. 

Trouver la circonférence d'un cercle
Teneur
La circonférence d`un cercle est la distance autour de son bord. Si un cercle a une circonférence de 2 miles, alors vous devez faire le tour du cercle 2 miles avant de revenir à votre point de départ. Cependant, si vous travaillez sur un problème géométrique, vous n`avez pas à vous lever de votre chaise. Lisez attentivement le problème pour savoir si le "rayon" (r), le "diamètre" (d) ou la "surface" (A) du cercle est donné, puis trouvez la partie de cet article qui est destinée à vous aider avec la tâche. Il existe également des instructions pour trouver le périmètre d`un objet circulaire existant que vous souhaitez mesurer.
Pas
Méthode 1 sur 4: Détermination du périmètre à l`aide du rayon

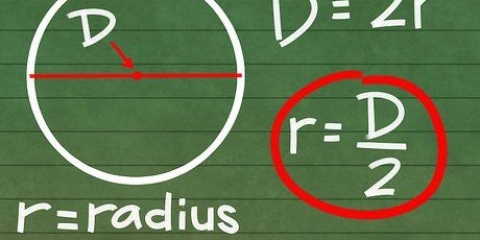
1. Dessinez un `rayon` sur le cercle. Tracez une ligne du centre du cercle à n`importe quelle position sur le bord du cercle. Cette ligne est le « rayon » du cercle, souvent écrit « r » dans les équations et formules mathématiques.
- `Remarque: si le rayon n`est pas donné dans le problème mathématique, alors ce ne sont peut-être pas les bonnes instructions. Voir si celles concernant le diamètre ou la surface sont plus utiles pour l`affectation.

2. Tracez un "diamètre" sur le cercle. Prolongez la ligne que vous venez de tracer pour qu`elle atteigne le bord du cercle de l`autre côté. Tu viens de dessiner un deuxième rayon. Les deux rayons ajoutés ont une longueur de `2 x le rayon`, écrit comme 2r. La longueur de cette ligne est le « diamètre » du cercle, souvent écrit comme ré.

3. Comprendre π (`pi`). Le symbole ??, aussi écrit comme pi n`est pas un nombre magique qui se trouve être utilisé dans ce genre de problèmes mathématiques. En fait, le nombre π a été à l`origine « découvert » en mesurant des cercles : si vous mesurez la circonférence d`un cercle (par exemple avec un ruban à mesurer), puis divisez par le diamètre, vous obtenez toujours le même nombre. Ce nombre est inhabituel car il ne peut pas être écrit sous la forme d`une simple fraction ou d`un nombre décimal. Au lieu de cela, nous pouvons l`arrondir à un nombre comme 3,14, ce qui est "assez bon".

4. Écrire la définition de comme un problème d`algèbre. Comme expliqué ci-dessus, signifie simplement "le nombre que vous obtenez lorsque vous divisez la circonférence par le diamètre". Sous la forme d`une formule mathématique, c`est : = C / j. Puisque nous savons que le diamètre est égal à 2 x le rayon, nous pouvons également écrire ceci comme = C / 2r.

5. Modifiez ce problème pour que vous résolviez ce problème pour le périmètre C. Nous voulons savoir quel est le périmètre (C dans ce problème de maths). Si vous multipliez les deux côtés par 2r vous obtenez x 2r = (C/2r) x 2r, et c`est pareil que 2πr = C.

6. Substituer les nombres à résoudre pour C. Maintenant, nous savons que 2πr = C. Revenez au problème mathématique d`origine pour voir ce que r (le rayon) est. Remplacez ensuite π par 3.14, ou utilisez le bouton de votre calculatrice pour obtenir une réponse plus précise. Calculez 2πr avec ces nombres. La réponse que vous obtenez est la circonférence.
Méthode 2 sur 4: Détermination de la circonférence à l`aide du diamètre

1. Comprendre ce qu`est un "diamètre". Placez votre crayon sur le bord du cercle. Tracez une ligne passant par le centre du cercle et le bord de l`autre côté. Cette ligne (d`un bord à l`autre et passant par le centre) est le « diamètre » du cercle, souvent écrit comme ré dans les problèmes de maths.
- La ligne passe par le centre exact du cercle, pas n`importe où dans le cercle.
- Remarque: Si l`énoncé n`indique pas la longueur du diamètre, utilisez une autre méthode.

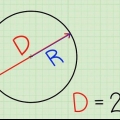
2. Apprenez ce que d = 2r signifie. Le « rayon » du cercle, également écrit comme r, est la distance du centre au bord du cercle. Puisque le diamètre passe par le cercle d`un bord à l`autre, par le centre, le diamètre est égal à deux rayons. Une façon simple d`écrire ceci est d = 2r. Cela signifie que vous ré peut toujours remplacer par 2r dans un problème de maths, et vice versa.

3. Comprendre π (`pi`). Le symbole ??, aussi écrit comme pi n`est pas un nombre magique qui se trouve être utilisé dans ce genre de problèmes mathématiques. En fait, le nombre π a été à l`origine « découvert » en mesurant des cercles : si vous mesurez la circonférence d`un cercle (par exemple avec un ruban à mesurer), puis divisez par le diamètre, vous obtenez toujours le même nombre. Ce nombre est inhabituel car il ne peut pas être écrit sous la forme d`une simple fraction ou d`un nombre décimal. Au lieu de cela, nous pouvons l`arrondir à un nombre comme 3,14, ce qui est "assez bon".

4. Écrire la définition de comme un problème d`algèbre. Comme expliqué ci-dessus, signifie simplement "le nombre que vous obtenez lorsque vous divisez la circonférence par le diamètre". Sous la forme d`une formule mathématique c`est : π = circonférence / diamètre ou = C / j.

5. Modifiez ce problème pour que vous résolviez ce problème pour le périmètre C. Nous voulons savoir quel est le périmètre, nous devons donc obtenir C d`un seul côté. Pour ce faire, multipliez chaque côté de l`équation par d :

6. Remplacez les nombres et résolvez pour C. Revenez au problème d`origine pour voir quel est le diamètre et remplacez le d dans cette équation par ce nombre. Remplacez π par un arrondi comme 3.14, ou utilisez le bouton de votre calculatrice pour un résultat plus précis. Multipliez les valeurs et d ensemble et vous obtenez le périmètre C.
Méthode 3 sur 4: Trouver le périmètre à l`aide de la zone

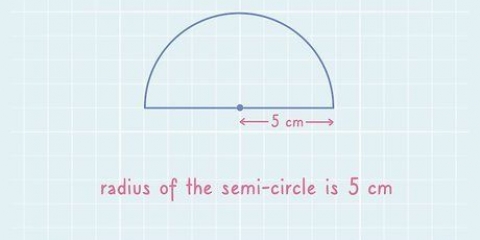
1. Comprendre comment se calcule l`aire d`un cercle. Généralement la zone (une) d`un cercle non mesuré directement. Au lieu de cela, vous mesurez le rayon (r) du cercle, puis calculez l`aire avec la formule A = r. La raison pour laquelle cette formule a du sens est un peu difficile à expliquer, mais vous pouvez en savoir plus via ce lien si vous êtes intéressé et disposé à aller au fond d`une algèbre plus lourde.
- Remarque: Si le problème de maths ne mentionne pas l`aire du cercle, vous devrez peut-être utiliser une méthode différente de cet article.

2. Apprendre une formule pour calculer la circonférence. La circonférence (C) est la distance autour du cercle. Vous le calculez généralement avec la formule C=2πr, mais parce qu`on ne sait pas encore quel est le rayon (r), nous devrons passer un certain temps à déterminer la valeur de r avant de pouvoir résoudre l`équation.

3. Utilisez la formule de la zone pour obtenir r d`un côté. Puisque A = r, nous pouvons réorganiser cette formule pour résoudre r à la place. Si vous trouvez les étapes ci-dessous difficiles à suivre, essayez d`abord des problèmes d`algèbre plus simples ou pratiquez certaines techniques pour comprendre l`algèbre.

4. Modifiez la formule du périmètre en utilisant ce que vous avez trouvé. Chaque fois que vous avez une équation comme r = (A/π), pouvez-vous remplacer un côté de l`équation par l`autre ?. Utilisons cette technique pour obtenir la formule de circonférence ci-dessus, C=2πr, changer. Pour ce problème, nous ne connaissons pas la valeur de r, mais nous connaissons celle de A. Modifions-le comme ceci pour que le problème soit résolu :

5. Remplacez les nombres pour trouver le périmètre. Utilisez la zone donnée dans le problème pour trouver le périmètre du périmètre. Par exemple, si la zone (une) d`un cercle est de 15 unités carrées, puis remplissez 2π(√(15/π)) dans ta calculatrice. N`oubliez pas les parenthèses.
Méthode 4 sur 4: Détermination de la circonférence d`un cercle réel

1. Utilisez cette méthode pour mesurer de vrais objets circulaires. Vous pouvez mesurer la circonférence des cercles que vous trouvez dans le monde réel, pas seulement dans les problèmes. Essayez-le sur une roue de vélo, une pizza ou une pièce de monnaie.

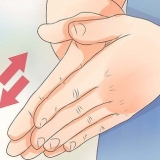
2. Prenez un morceau de ficelle et une règle. La ficelle doit être suffisamment longue pour envelopper le cercle une fois et suffisamment flexible pour s`adapter parfaitement. Vous aurez besoin de quelque chose pour mesurer la corde plus tard, comme une règle ou un ruban à mesurer. La ficelle sera plus facile à mesurer si la règle est plus longue que la longueur de la ficelle.

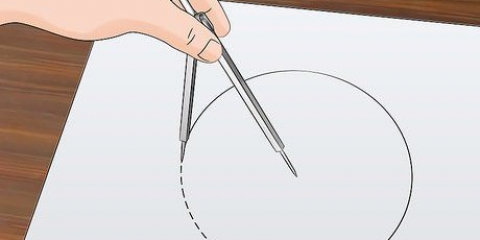
3. Enroulez la ficelle une fois autour du cercle. Commencez par placer une extrémité de la ficelle le long du bord du cercle. Enroulez la corde autour du cercle et tirez dessus. Si vous mesurez une pièce de monnaie ou un autre objet fin, vous ne pourrez peut-être pas serrer la ficelle autour de celle-ci. Posez l`objet circulaire à plat et disposez la ficelle autour, aussi serrée que possible.

4. Marquer ou couper la ficelle. Trouvez l`endroit sur la chaîne où la boucle se termine et touche la fin de la chaîne avec laquelle vous avez commencé. Marquez cet endroit avec un marqueur, ou coupez la corde à cet endroit.

5. Desserrez la corde et mesurez-la avec une règle. Prenez la corde enroulée et mesurez-la avec une règle. Si vous avez utilisé un marqueur, mesurez uniquement de la fin de la chaîne au marqueur. C`est la partie de la ficelle qui entoure le cercle, et puisque la circonférence d`un cercle n`est que la distance autour du cercle, vous avez trouvé la réponse! La longueur de cette corde est égale à la circonférence du cercle.
Des astuces
- Vous pouvez écrire le pluriel de rayon comme rayons ou comme rayons.
Articles sur le sujet "Trouver la circonférence d'un cercle"
Оцените, пожалуйста статью
Populaire