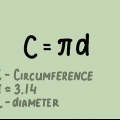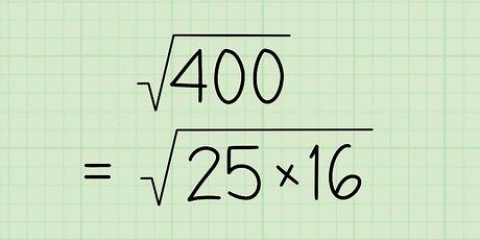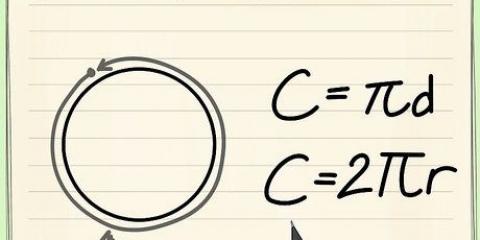Disons que l`aire du cercle est de 500 cm. Ensuite, vous élaborez l`équation comme suit : 2√3,14 x 500. 
Si le calcul est égal à 2√3,14 x 500, alors vous calculez d`abord 3,14 x 500 = 1570. Calculez ensuite 2√1,570. 
La racine carrée de 1570 est 39,6. 
Calculez 39,6 x 2 = 79,2. Cela signifie que la circonférence est de 79,2 cm, ce qui résout la formule. 

Supposons que l`aire du cercle est de 200 cm. L`équation devient alors 200 = 3,14 x R. 
Si vous divisez 200 par 3,14, le résultat est 63,7. Donc la nouvelle équation est 63,7 = R. 
La racine carrée de 63,7 est 7,9. L`équation devient alors 7,9 = R, ce qui signifie que le rayon du cercle est de 7,9. Cela vous donnera toutes les informations dont vous avez besoin pour trouver le périmètre. 
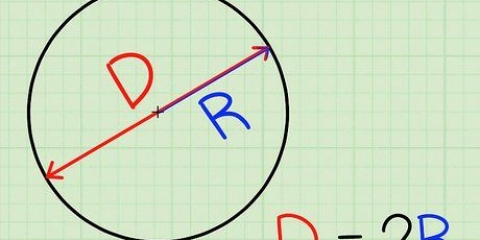
Utilisez la première option, 7,9 x 2 = 15,8, le diamètre du cercle. Ce diamètre multiplié par 3,14 est de 49,6. Pour la deuxième option, le calcul devient 2 x 3,14 x 7,9. Vous calculez d`abord 2 x 3,14 = 6,28, et cela multiplié par 7,9 est de 49,6. Remarquez comment les deux méthodes vous donnent la même réponse.
Calculer la circonférence à l'aide de la surface
Teneur
La formule pour calculer la circonférence (C) d`un cercle, C = πD ou C = 2πR, est simple si vous connaissez le diamètre (D) ou le rayon (R) du cercle. Mais que faites-vous si vous ne connaissez que l`aire du cercle? Comme beaucoup de choses en mathématiques, il existe plusieurs solutions à ce problème. La formule C = 2√πA est conçue pour trouver la circonférence d`un cercle en utilisant l`aire (A). Vous pouvez également inverser l`équation A = πR pour trouver R, puis entrer R dans l`équation du périmètre. Les deux équations donnent le même résultat.
Pas
Méthode 1 sur 2: Utilisation de l`équation du périmètre

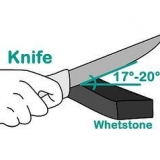
1. Utilisez la formule C=2√πA pour résoudre le problème. Cette formule calcule la circonférence d`un cercle si vous ne connaissez que son aire. C représente le périmètre et A pour la zone. Écrivez cette formule pour commencer à résoudre le problème.
- Le symbole π, qui signifie pi, est un nombre décimal répété avec (maintenant) des milliers de chiffres après la virgule. Pour plus de simplicité, utilisez 3,14 comme valeur de pi.
- Puisque vous devez de toute façon convertir pi en sa forme numérique, utilisez 3.14 dans l`équation depuis le début. Écrivez-le comme C = 2√3,14 x A.

2. Inclure la zone comme A dans l`équation. Puisque vous connaissez déjà l`aire du cercle, c`est la valeur de A. Procédez ensuite à la résolution du problème en utilisant l`ordre des opérations.

3. Multiplier pi par l`aire du cercle. Dans l`ordre des opérations, les opérations dans le symbole de la racine carrée viennent en premier. Multipliez pi par l`aire du cercle que vous avez branché. Puis branchez ce résultat dans l`équation.

4. Particulierracine carrée de la somme. Il existe plusieurs façons de calculer la racine carrée. Si vous utilisez une calculatrice, appuyez sur la fonction et tapez le nombre. Vous pouvez également résoudre le problème à la main en utilisant des facteurs premiers.

5. Multipliez la racine carrée par 2 pour trouver le périmètre. Enfin, vous terminez le calcul en multipliant le résultat par 2. Cela renvoie un nombre final, la circonférence.
Méthode 2 sur 2: Résoudre le problème à l`envers

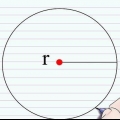
1. Utilisez la formule A = πR dans. C`est la formule de l`aire d`un cercle. A représente l`aire et R le rayon. Normalement, vous l`utiliseriez si vous connaissiez le rayon, mais vous pouvez également remplir la zone pour résoudre l`équation.
- Encore une fois, utilisez 3,14 comme valeur arrondie pour pi.

2. Entrez la zone comme valeur pour A. Utiliser l`aire du cercle dans l`équation. Placez ceci à gauche de l`équation comme valeur pour A.

3. Divisez les deux côtés de l`équation par 3,14. Pour résoudre ce genre d`équation, il faut éliminer progressivement les étapes à droite en faisant les opérations inverses. Puisque vous connaissez la valeur de pi, vous divisez chaque côté par cette valeur. Cela élimine pi à droite et vous donne une nouvelle valeur numérique à gauche.

4. Particulierracine carrée du résultat pour obtenir le rayon du cercle. Ensuite, l`exposant du côté droit de l`équation est éliminé. Le contraire de "exponentiation" est de trouver la racine carrée du nombre. Trouver la racine carrée de chaque côté de l`équation. Cela supprime l`exposant à droite et met le rayon à gauche.

5.Déterminer la circonférence du cercle en utilisant le rayon. Il existe deux formules pour trouver le périmètre (C). Le premier est C = πD, où D est le diamètre. Multipliez le rayon par 2 pour trouver le diamètre. La seconde est C = 2πR. Multipliez 3,14 par 2 puis multipliez le résultat par le rayon. Les deux formules vous donneront le même résultat.
Articles sur le sujet "Calculer la circonférence à l'aide de la surface"
Оцените, пожалуйста статью
Similaire
Populaire