Calculer l'aire d'une ellipse : 5 étapes (avec photos)

Teneur

Pas
- Partie 1 sur 2: Calcul de la superficie
- Partie 2 sur 2: Comprendre pourquoi cela fonctionne
Des astuces

Une ellipse est une forme bidimensionnelle que vous connaissez peut-être déjà de la classe de géométrie, qui ressemble à un cercle allongé. Calculer l`aire d`une ellipse est facile quand on connaît la longueur du plus grand rayon et du plus petit rayon.

Pas

Partie 1 sur 2: Calcul de la superficie

Image intitulée Calculer l`aire d`une ellipse Étape 1

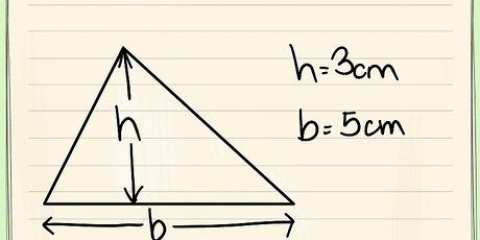
1. Trouver le plus grand rayon de l`ellipse. C`est la distance entre le centre de l`ellipse et le bord extrême de l`ellipse. Considérez ceci comme le rayon de la partie « épaisse » de l`ellipse. Mesurez ceci ou recherchez l`étiquette appropriée dans le tableau. Nous appelons cette valeur une.

Vous pouvez également appeler cela le « grand axe principal ».

Image intitulée Calculer l`aire d`une ellipse Étape 2

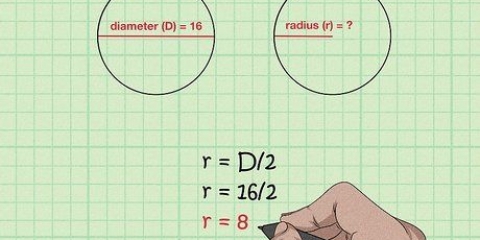
2. Trouver le plus petit rayon. Comme vous l`avez peut-être deviné, le plus petit rayon est la distance entre le centre et le point le plus proche sur le bord. Nous appelons cette valeur b.

Ce rayon est perpendiculaire au plus grand rayon, mais vous n`avez pas besoin de mesurer les angles pour ce problème.

Vous pouvez également appeler ce rayon le « grand axe mineur ».

Image intitulée Calculer l`aire d`une ellipse Étape 3

3. Multiplier par pi. L`aire de l`ellipse est une X b X. Puisque vous multipliez deux unités de longueur ensemble, votre réponse est un carré.

Par exemple, si une ellipse a un plus grand rayon de 5 et un plus petit rayon de 3, alors l`aire de l`ellipse est de 3 x 5 x π, soit environ 47 unités au carré.

Si vous n`avez pas de calculatrice ou si votre calculatrice n`a pas de symbole , utilisez « 3.14 » comme valeur pour pi.

Partie 2 sur 2: Comprendre pourquoi cela fonctionne

Image intitulée Calculer l`aire d`une ellipse Étape 4

1. Considérons l`aire d`un cercle. Vous vous souviendrez peut-être que le aire d`un cercle est égal àr, qui est le même que x r X r. Supposons que nous voulions déterminer l`aire d`un cercle comme s`il s`agissait d`une ellipse? Nous mesurons le rayon dans une direction: r. Mesurez-le avec des angles droits : aussi r. Appliquez ceci à la formule de l`aire d`une ellipse : π x r x r! Il s`avère qu`un cercle n`est qu`un type spécifique d`ellipse.

Image intitulée Calculer l`aire d`une ellipse Étape 5

2. Imaginez un cercle aplati. Imaginez qu`un cercle est imprimé en forme d`ellipse. Au fur et à mesure que le cercle se comprime de plus en plus, un rayon se raccourcit et l`autre s`allonge. La zone reste la même, car rien ne sort du cercle. Tant que nous utilisons les deux rayons dans l`équation, le « serrer » et « l`étirement » s`annuleront et nous obtiendrons toujours la bonne réponse.