Superficie = 1/2 x (3 cm x 5 cm) 
Superficie = 1/2 x (3 cm x 5 cm) Superficie = 1/2 x 15 cm Superficie = 7.5 cm 

Aire = √{6 (6 - 3)(6 - 4)(6 - 5)} 
6 - 3 = 3 6 - 4 = 2 6 - 5 = 1 Aire = {6 (3)(2)(1)} 









Aire = 1/2(b)(c) x sin A Aire = 1/2(150)(231) x sin A 
Aire = 1/2(150)(231) x sin A Aire = 1/2 (34 650) x sin A Aire = 17,325 x sin A Superficie = 17 325 x .8386705 Superficie = 14,530 cm
Calculer l'aire d'un triangle
Teneur
Bien que la méthode la plus courante pour calculer l`aire d`un triangle consiste à multiplier sa demi-base par sa hauteur, il existe un certain nombre d`autres façons de calculer l`aire d`un triangle, en fonction des données disponibles. Cela comprend la longueur des trois côtés, la longueur d`un côté d`un triangle équilatéral et la longueur des deux côtés ainsi que l`angle inclus. Lisez ici comment vous pouvez calculer l`aire d`un triangle en utilisant ces données.
Pas
Méthode 1 sur 4: Avec la base et la hauteur

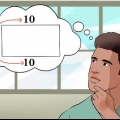
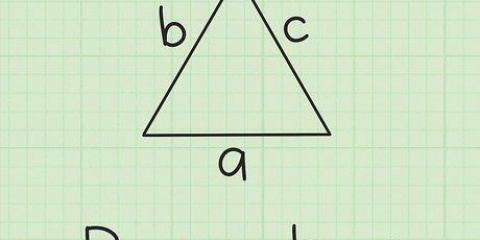
1. Déterminez la base et la hauteur de votre triangle. La base du triangle est la longueur d`un côté, qui est généralement le côté inférieur du triangle. La hauteur est la longueur de la base au coin supérieur du triangle, qui est perpendiculaire à la base. Dans un triangle rectangle, la base et la hauteur sont les deux côtés qui se rencontrent à un angle de 90 degrés. Mais, dans un autre triangle, comme on le voit ci-dessous, la ligne d`altitude traversera la forme.
- Une fois que vous avez déterminé la base et la hauteur du triangle, vous êtes prêt à commencer à utiliser la formule.

2. Écrivez la formule pour trouver l`aire d`un triangle. La formule pour ce type de problème est Aire = 1/2 (base x hauteur), ou 1/2(soutien-gorge). Une fois que vous avez tout noté, vous pouvez commencer à remplir la longueur de la hauteur et de la base.

3. Entrer les valeurs de base et de hauteur. Trouvez la base et la hauteur du triangle et utilisez ces valeurs dans l`équation. Dans cet exemple, la hauteur du triangle est de 3 cm et la base du triangle est de 5 cm. Voici à quoi ressemblerait la formule après avoir entré ces valeurs :

4. Résous l`équation. Vous pouvez d`abord multiplier la hauteur par la base car ces valeurs sont entre parenthèses. Ensuite, vous multipliez le résultat par 1/2. N`oubliez pas que vous donnerez la réponse en mètres carrés car vous travaillez dans un espace à deux dimensions. Voici comment résoudre ce problème pour la réponse finale :
Méthode 2 sur 4: Utilisation de la longueur de chaque côté (formule de Heron)

1. Calculer le demi-périmètre (semi-périmètre) du triangle. Pour trouver le demi-périmètre du triangle, il suffit d`additionner tous les côtés et de diviser le résultat par deux. La formule pour trouver le demi-périmètre d`un triangle est la suivante : demi-périmètre = (longueur du côté a + longueur du côté b + longueur du côté c) / 2, ou s = (a + b + c) / 2. Étant donné que les trois longueurs du triangle rectangle sont données, 3 cm, 4 cm et 5 cm, vous pouvez les insérer directement dans les formules et résoudre le problème du demi-périmètre :
- s = (3 + 4 + 5)/2
- s = 12/2
- s = 6

2. Entrez les valeurs correctes dans la formule pour trouver l`aire d`un triangle. Cette formule pour trouver l`aire d`un triangle est aussi appelée formule de Heron et se présente ainsi : Aire = √{s (s - a)(s - b)(s - c)}. Nous répétons l`étape précédente où s la demi-circonférence est et une, b, et c les trois côtés du triangle. Utilisez la séquence d`opérations suivante : commencez par résoudre tout ce qui est entre parenthèses, puis tout sous le signe radical, et enfin la racine carrée elle-même. Voici à quoi ressemblera cette formule lorsque vous aurez entré toutes les valeurs connues :

3. Soustraire les valeurs entre parenthèses. Donc : 6 - 3, 6 - 4 et 6 - 5. Voici le résultat sur papier :

4. Multiplier les résultats de ces opérations. Multipliez 3 x 2 x 1 pour obtenir 6 comme réponse. Il faut multiplier ces nombres entre eux avant de les multiplier par 6 car ils sont entre parenthèses.

5. Multiplier le résultat précédent par la moitié de la circonférence. Multipliez ensuite le résultat, 6, par la demi-circonférence, qui est également 6. 6 x 6 = 36.

6. Calculer la racine carrée. 36 est un carré parfait et √36 = 6. N`oubliez pas l`unité avec laquelle vous avez commencé : les centimètres. Exprimez la réponse finale en centimètres carrés. L`aire du triangle de côtés 3, 4 et 5 est de 6 cm.
Méthode 3 sur 4: Utilisation d`un côté d`un triangle rectangulaire

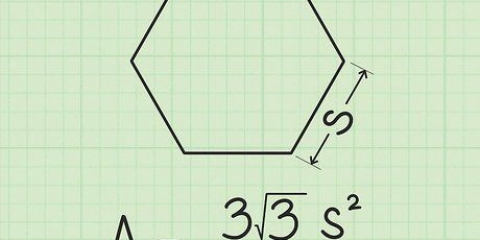
1. Trouver le côté du triangle équilatéral. Un triangle équilatéral a des côtés de même longueur et des angles égaux. Vous savez que vous avez affaire à un triangle équilatéral, soit parce que c`est une donnée, soit parce que vous savez que tous les angles et tous les côtés ont la même valeur. La valeur d`un des côtés de ce triangle est de 6 cm. Notez ceci.
- Si vous savez que vous avez affaire à un triangle équilatéral mais que seul le périmètre est connu, il suffit de diviser cette valeur par 3. Par exemple, la longueur d`un côté d`un triangle équilatéral de périmètre 9 est très simplement 9/3, ou 3.

2. Écrivez la formule pour trouver l`aire d`un triangle équilatéral. La formule pour ce type de problème est aire = (s^2)(√3)/4. Noter que s « soie » signifie.

3. Appliquer la valeur d`un côté à l`équation. Calculez d`abord le carré du côté de valeur 6, pour obtenir 36. Trouvez ensuite la valeur de 3, si la réponse doit être donnée en décimales. Entrez maintenant √3 dans votre calculatrice pour obtenir 1.732 pour obtenir. Divisez ce nombre par 4. Notez que vous pouvez également diviser 36 par 4 puis multiplier par √3 -- l`ordre des opérations n`a aucun effet sur la réponse.

4. Résoudre. Maintenant, il s`agit principalement de compter. 36 x √3/4 = 36 x .433 = 15.59 cm L`aire d`un triangle équilatéral de 6 cm de côté est de 15.59cm.
Méthode 4 sur 4: Utilisation de la longueur des deux côtés et de l`angle inclus

1. Trouver la valeur des longueurs des deux côtés et l`angle inclus. L`angle inclus est l`angle entre les deux côtés connus du triangle. Vous devez connaître ces valeurs pour trouver l`aire d`un triangle en utilisant cette méthode. Supposons un triangle avec les dimensions suivantes :
- angle A = 123º
- côté b = 150 cm
- côté c = 231 cm

2. Écrivez la formule pour trouver l`aire du triangle. La formule pour trouver l`aire d`un triangle avec deux côtés connus et un angle inclus connu est la suivante : Aire = 1/2(b)(c) x sin A. Dans cette équation représentent "b" et "c" les longueurs des côtés et "une" le coin. Vous devriez toujours prendre le sinus de l`angle dans cette équation.

3. Remplissez les valeurs dans l`équation. Voici à quoi ressemble l`équation une fois ces valeurs saisies :

4. Résoudre. Pour résoudre cette équation, multipliez d`abord les côtés et divisez le résultat par deux. Multipliez ensuite ce résultat par le sinus de l`angle. La valeur du sinus peut être trouvée avec votre calculatrice. N`oubliez pas de donner votre réponse en unités cubes. Voici comment procéder :
Des astuces
- Si vous ne comprenez pas pourquoi la formule de base - hauteur fonctionne de cette façon, voici une courte explication. Si vous faites un deuxième triangle identique et que vous le placez l`un à côté de l`autre, il formera soit un rectangle (deux triangles rectangles) soit un parallélogramme (deux triangles non rectangles). Pour trouver l`aire d`un rectangle ou d`un parallélogramme, il suffit de multiplier la base par la hauteur. Puisqu`un triangle est égal à la moitié d`un rectangle ou d`un parallélogramme, il s`ensuit que l`aire d`un triangle est égale à la moitié d`une base multipliée par sa hauteur.
Articles sur le sujet "Calculer l'aire d'un triangle"
Оцените, пожалуйста статью
Populaire