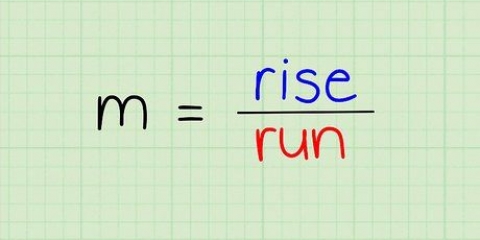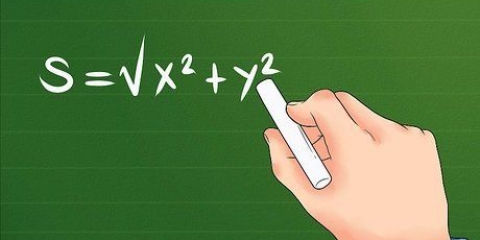Notez, cependant, que si les unités de temps utilisées dans votre valeur de vitesse moyenne sont différentes de celles de votre valeur de temps, vous devrez convertir l`une ou l`autre pour correspondre. Par exemple, si une vitesse moyenne est mesurée en km/h et le temps est en minutes, vous devrez diviser le temps par 60 pour le convertir en heures. Résolvons notre exemple de problème. 120 km/h × 0,5 h = 60 km. Notez que les unités de temps (heures) tomber contre les unités au dénominateur de la vitesse moyenne (heures), ne laissant que les unités de distance (km). 
Supposons que nous sachions qu`une voiture a parcouru 60 km en 50 minutes, mais nous n`avons aucune valeur pour la vitesse moyenne en conduisant. Dans ce cas, nous pouvons utiliser la variable sgemme isolent dans l`équation de base pour la distance, et nous obtenons sgemme = d/t pour obtenir. Ensuite on calcule 60 km/50 minutes = 1,2 km/min. Notez que dans notre exemple, notre réponse pour la vitesse a une unité inhabituelle (km/minute). Pour obtenir votre réponse sous la forme la plus courante de km/h, multipliez-la par 60 minutes/h et obtenez `72 km/h pour obtenir. 
Exemple : Dans l`exemple de problème ci-dessus, nous avons conclu que pour parcourir 60 km en 50 minutes, il faudrait parcourir 72 km/h. Cependant, cela n`est vrai que si nous voyageons à une vitesse pendant tout le trajet. Par exemple, en faisant la moitié du trajet à 80 km/h et l`autre moitié à 64 km/h, on fait quand même 60 km en 50 minutes — 72 km/h = 60 km/50 min = ????? Solutions mathématiques l`utilisation de dérivées est souvent un meilleur choix que la formule de distance pour définir la vitesse d`un objet dans des situations réelles, car des changements de vitesse sont probables. 

Notez que cette formule utilise des valeurs absolues (le symbole |). Les valeurs absolues signifient simplement que les termes dans les symboles deviennent positifs lorsqu`ils sont négatifs. Par exemple, disons que nous nous arrêtons sur un tronçon de route parfaitement rectiligne le long du chemin. S`il y a une petite ville à 5 km devant nous et une ville à 1 km derrière nous, à quelle distance sont les deux villes ?? Si nous prenons la ville 1 comme x1 = considérer 5 et la ville 2 comme x2 = -1, alors on peut trouver d, la distance entre les deux villes, comme suit : d = |x2 - X1| = |-1 - 5| = |-6| = 6 km. 
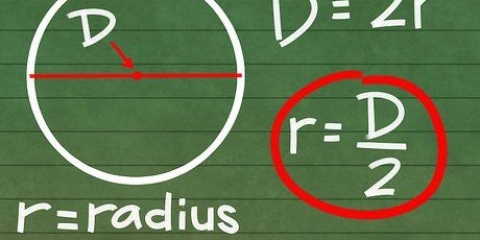
La formule de distance dans l`espace à deux dimensions utilise le théorème de Pythagore, qui stipule que l`hypoténuse d`un triangle rectangle est égale à la racine carrée des deux autres côtés. Par exemple, disons que nous avons deux points dans le plan x-y : (3, -10) et (11, 7) qui représentent respectivement le centre d`un cercle et un point sur le cercle. Pour trouver la distance en ligne droite entre ces deux points, nous pouvons résoudre les problèmes suivants : d = ((x2 - X1) + (y2 - oui1)) d = ((11 - 3) + (7 - -10)) d = (64 + 289) d = (353) = 18,79 
Exemple : Disons qu`en tant qu`astronaute planant dans l`espace près de deux astéroïdes. L`un est à environ 8 km devant nous, 2 km à notre droite et 5 km en dessous de nous, tandis que l`autre est à 3 km derrière nous, 3 km à notre gauche et 4 km au-dessus de nous. Si nous représentons les positions de ces astéroïdes avec les coordonnées (8.2,-5) et (-3,-3.4), nous pouvons trouver la distance entre les deux comme suit : d = ((-3 - 8) + (-3 - 2) + (4 - -5)) d = ((-11) + (-5) + (9)) d = (121 + 25 + 81) d = (227) =15,07 km
Calculer la distance
Teneur
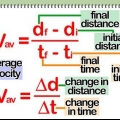
La distance, souvent appelée la variable ré, est une mesure de l`espace occupé par une droite entre deux points. La distance peut faire référence à l`espace entre deux points fixes (par exemple, la taille d`une personne est la distance entre le bas de ses pieds et le haut de sa tête) ou peut faire référence à l`espace entre la position actuelle d`un objet et son emplacement de départ. La plupart des problèmes de distance peuvent être résolus avec les équations d = sgemme × t où d est la distance, sgemme la vitesse moyenne, et t le temps, ou l`équation d = ((x2 - X1) + (y2 - oui1)), où (x1, oui1) et (x2, oui2) sont les coordonnées x et y de deux points.
Pas
Méthode 1 sur 2: Déterminer la distance avec la vitesse et le temps moyens

1. Déterminer les valeurs pour la vitesse moyenne et le temps. Lorsqu`on essaie de trouver la distance qu`un objet en mouvement a parcourue, deux informations sont vitales pour faire ce calcul : la vitesse` (ou l`amplitude de la vitesse) et letemps où l`objet a été déplacé. Avec ces données, il est possible de trouver la distance parcourue par l`objet, en utilisant la formule d = sgemme × t.
- Pour mieux comprendre l`application de la formule de distance, dans cette section, nous allons résoudre un exemple de problème. Disons que nous roulons à environ 120 km/h et que nous voulons savoir quelle distance nous parcourrons en une demi-heure. De 120 km/h comme notre valeur pour la vitesse moyenne et 0,5 heure comme valeur du temps, nous allons résoudre ce problème à l`étape suivante.

2. Multiplier la vitesse moyenne par le temps. Une fois que vous connaissez la vitesse moyenne d`un objet en mouvement et le temps qu`il a mis pour se déplacer, il est relativement facile de trouver la distance qu`il a parcourue. Il suffit de multiplier ces deux valeurs ensemble pour obtenir votre réponse.

3. Modifier l`équation à résoudre pour les autres variables. La simplicité de l`équation de distance de base (d = sgemme × t) permet d`utiliser assez facilement l`équation pour trouver les valeurs des variables en plus de la distance. Isolez la variable que vous souhaitez résoudre selon les règles de base de mathématiques, puis entrez les valeurs des deux autres variables, pour trouver la valeur de la troisième. En d`autres termes, pour trouver la vitesse moyenne de votre objet, utilisez l`équation sgemme = d/t et pour trouver le temps qu`un objet a parcouru, utilisez l`équation t = d/sgemme.

4. Notez que la variable `sgemme` dans la formule de distance fait référence à moyenne vitesse. Il est important de comprendre que la formule de distance standard fournit une image simplifiée du mouvement d`un objet. La formule de distance suppose que l`objet en mouvement a un vitesse constante a — en d`autres termes, cela suppose que l`objet en mouvement se déplace à une vitesse « uniforme », immuable. Pour les problèmes mathématiques abstraits, tels que ceux rencontrés dans un cadre académique, il est parfois encore possible de modéliser le mouvement d`un objet en utilisant cette hypothèse. Dans la vraie vie, cependant, ce modèle ne représente souvent pas avec précision le mouvement des objets en mouvement, qui en réalité peuvent accélérer, décélérer, s`arrêter et s`inverser au fil du temps.
Méthode 2 sur 2: Détermination de la distance entre deux points

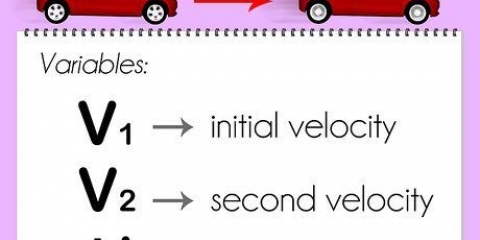
1. Détermination de deux points dans un espace plat. Et si au lieu de déterminer la distance parcourue par un objet en mouvement, vous deviez déterminer la distance entre deux objets fixes? Dans de tels cas, la formule de distance basée sur la vitesse décrite ci-dessus ne sera d`aucune utilité. Heureusement, il existe une autre formule de distance pour trouver rapidement la distance la plus courte entre deux points. Cependant, pour cette formule, vous devez connaître les coordonnées des deux points. Si vous avez affaire à une distance unidimensionnelle (comme sur une droite numérique), vos coordonnées sont deux nombres, x1 et x2. Si vous avez affaire à une distance en deux dimensions, vous avez besoin de valeurs pour deux points (x,y), (x1,oui1) et (x2,oui2). Enfin, pour trois dimensions, vous avez besoin de valeurs pour (x1,oui1,z1) et (x2,oui2,z2).

2. Déterminer la distance sur une ligne en soustrayant la valeur des coordonnées des deux points. Calculer la distance unidimensionnelle entre deux points si vous connaissez la valeur de chaque point est facile. Utilisez simplement la formule d = |x2 - X1|. Dans cette formule, vous soustrayez x1 hors de x2 et prenez la valeur absolue de votre réponse pour trouver la distance entre x1 et x2 trouver. Normalement, vous utilisez la formule de distance unidimensionnelle lorsque les deux points se trouvent sur une droite numérique ou un axe.

3. Trouver la distance dans le plan en utilisant le théorème de Pythagore. Trouver la distance entre deux points dans un espace à deux dimensions est plus compliqué que dans une dimension, mais pas difficile. Utilisez simplement la formule d = ((x2 - X1) + (y2 - oui1)). Dans cette formule, vous soustrayez les deux coordonnées x, placez le résultat au carré, soustrayez les coordonnées y, placez le résultat au carré, ajoutez les deux résultats intermédiaires et calculez la racine carrée pour trouver la distance entre les deux points à trouver. Cette formule fonctionne dans le plan bidimensionnel — par exemple sur les cartes x/y standard.

4. Déterminer la distance tridimensionnelle en changeant la formule de la zone. En trois dimensions, les points ont également une coordonnée z en plus des coordonnées x et y. Pour trouver la distance entre deux points dans un espace tridimensionnel, utilisez d = ((x2 - X1) + (y2 - oui1) + (z2 - z1)). Il s`agit d`une forme modifiée de la formule de distance bidimensionnelle décrite ci-dessus qui prend également en compte les coordonnées z. En soustrayant les deux coordonnées z l`une de l`autre, en les plaçant dans le carré et en parcourant le reste de la formule comme décrit ci-dessus, vous pouvez être sûr que votre réponse finale reflète la distance tridimensionnelle entre les deux points.
Articles sur le sujet "Calculer la distance"
Оцените, пожалуйста статью
Populaire