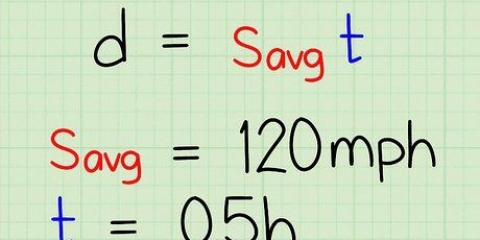N`oubliez pas non plus de relier le point de départ au point d`arrivée, en utilisant une ligne droite.C`est le déplacement que nous allons calculer. Par exemple, si un objet parcourt d`abord 300 mètres vers l`est puis 400 mètres vers le nord, un triangle rectangle se forme. AB est le premier côté et BC est le deuxième côté du triangle.AC est l`hypoténuse du triangle et sa valeur est le déplacement de l`objet. Dans cet exemple, les deux directions sont "est" et "Nord." 
Par exemple, x = 300 et y = 400.Votre équation ressemble maintenant à ceci : s = √300² + 400². 
Par exemple : s = 90000 + 160000.s = 250000.s = 500.Vous savez maintenant que le déplacement est égal à 500 mètres. 

L`équation ressemblera à ceci : s = 1/2(20 + 23)45. 
Pour cette équation, peu importe si vous échangez accidentellement les vitesses initiale et finale. Parce que vous ajoutez d`abord ces valeurs ensemble, cela n`a pas d`importance. Mais dans d`autres équations, l`échange des vitesses initiale et finale peut affecter la réponse finale ou la valeur du déplacement. Votre équation ressemble maintenant à ceci : s = 1/2(43)45.Divisez d`abord 43 par 2, ce qui donne 21,5 comme réponse. Multipliez 21,5 par 45, ce qui donne 967,5 mètres comme réponse.967,5 est le déplacement de la voiture, vu depuis le point de départ. 

Sur la base de l`exemple ci-dessus, votre équation devrait maintenant ressembler à ceci : s = 25(4) + 1/2(3)4².Cela peut certainement aider si vous mettez des parenthèses autour des valeurs d`accélération et de temps pour séparer les nombres les uns des autres. 
Regardons de plus près l`équation : s = 25(4) + 1/2(3)4². L`ordre est : 4² = 16 ; alors 16 x 3 = 48 ; alors 25 x 4 = 100 ; et si dernier 48/2 = 24. L`équation ressemble maintenant à ceci : s = 100 + 24.Après addition, cela donne s = 124, donc le déplacement est de 124 mètres. 

Exemple de devoir : une fille est assise sur un manège. Son siège est à une distance de 1 mètre du centre du cercle (le rayon). Si la fille se déplace le long d`un arc de cercle de 1,5 mètre (déplacement linéaire), quel est son déplacement angulaire? L`équation ressemble à ceci : = 1.5/1. 
Après la division 1.5/1 il vous reste 1.5.Le déplacement angulaire de la fille est de 1,5 radians. Étant donné que le déplacement angulaire indique de combien un objet a été tourné depuis sa position d`origine, il est nécessaire de le représenter en radians, et non en distance. Les radians sont des unités utilisées pour mesurer les angles. 

Le déplacement est aussi appelé "quantité de vecteur" appelé changement de position d`un objet par rapport à la direction dans laquelle l`objet se déplace. Supposons que vous marchiez 5 mètres vers l`est. Si vous marchez à nouveau 5 mètres vers l`ouest, vous vous déplacerez dans la direction opposée, retour à votre point de départ. Même si vous avez parcouru un total de 10 mètres, votre position n`a pas changé et votre déplacement est donc de 0 mètre. 
Imaginez un entraîneur de football rebondissant sur la touche.Tout en donnant des instructions aux joueurs, il a parcouru la ligne plusieurs fois, en va-et-vient. Si vous gardiez constamment un œil sur l`entraîneur, vous verriez la distance qu`il parcourt. Mais supposons que l`entraîneur s`arrête pour dire quelque chose à un défenseur? S`il est dans un endroit différent de son point de départ, alors tu regardes le mouvement du coach (à un certain moment). 
Un chemin courbe finira par vous conduire du point de départ au point final, mais ce n`est pas le chemin le plus court. Pour vous aider à visualiser cela, imaginez marcher en ligne droite et être arrêté par un pilier ou un autre obstacle. Tu ne peux pas traverser le pilier, alors tu le contournes. Même si vous vous retrouvez au même endroit que si vous étiez passé directement par le pilier, vous deviez quand même parcourir un plus long chemin pour vous y rendre. Bien que le déplacement soit de préférence en ligne droite, il est possible de mesurer le déplacement d`un objet qui "bien" se déplace le long d`un chemin tortueux. C`est ce qu`on appelle le "déplacement angulaire" et il peut être calculé en trouvant la distance la plus courte qui existe entre le point de départ et le point d`arrivée. 
Par exemple, supposons que vous marchiez 5 mètres vers l`est puis 3 mètres vers l`ouest. Bien que vous soyez techniquement à 2 mètres de votre point de départ, le déplacement est de -2 car vous vous déplacez dans la direction opposée à ce point.La distance sera toujours positive, car tu ne connais pas la distance que tu as parcourue "défait" peut faire. Un déplacement négatif ne signifie pas que le déplacement diminue. C`est simplement une façon d`indiquer que le mouvement est dans la direction opposée. 
Cela n`est donc possible que si vous vous déplacez en ligne droite depuis le point de départ, et sans changer de direction par la suite.Par exemple, supposons que vous habitiez à San Francisco, en Californie et que vous trouviez un emploi à Las Vegas, au Nevada. Vous devrez ensuite déménager à Las Vegas pour vivre plus près de votre travail. Si vous prenez l`avion, un vol direct de San Francisco à Las Vegas, vous avez parcouru 670 km et votre déplacement est donc de 670 km. Cependant, si vous voyagez en voiture de San Francisco à Las Vegas, votre distance peut toujours être de 670 km mais vous avez parcouru 906 km entre-temps.Étant donné que la conduite implique généralement un changement de direction (descente, emprunter un itinéraire différent), vous avez parcouru une distance beaucoup plus grande que la distance la plus courte entre les deux villes.
Calculer le déplacement
Teneur
Le terme déplacement en physique fait référence au changement plutôt qu`à un objet. Lors du calcul du déplacement, vous mesurez de combien un objet s`est déplacé, en fonction des données de la position de départ et de la position de fin. La formule que vous utilisez pour déterminer le déplacement dépend des variables qui sont données pour un problème. Suivez les étapes suivantes pour apprendre à calculer le déplacement d`un objet.
Pas
Partie 1 sur 5: Calcul du déplacement résultant

1. Utilisez la formule pour le déplacement résultant en utilisant l`unité de longueur utilisée pour spécifier la position de début et de fin. Bien que la distance soit différente du déplacement, une déclaration sur le déplacement résultant indiquera de combien "marraine" a jeté un objet. Utilisez ces unités de mesure pour calculer le déplacement, à quelle distance un objet est de son emplacement d`origine.
- L`équation du déplacement résultant est : s = x²+y²."s" signifie déplacement.X est la première direction dans laquelle l`objet se déplace et y est la deuxième direction dans laquelle l`objet se déplace. Si votre objet ne se déplace que dans 1 direction, alors y = 0.
- Un objet ne peut se déplacer que dans 2 directions maximum, car se déplacer le long de la ligne nord-sud ou est-ouest est considéré comme neutre.

2. Reliez les points selon l`ordre de mouvement et étiquetez ces points de A-Z.Utilisez une règle pour tracer des lignes droites d`un point à un autre.

3. Entrez les valeurs pour x² et y².Maintenant que vous connaissez la direction dans laquelle votre objet se déplace, vous pouvez commencer à renseigner les valeurs des variables pertinentes.

4. Établir l`équation. Calculez d`abord 300² puis 400², additionnez-les et soustrayez la racine carrée de la somme.
Partie 2 sur 5: Connaître le vecteur vitesse et la durée

1. Utilisez cette formule si le problème donne le vecteur vitesse et la durée. Il peut arriver qu`un problème de physique ne dise pas un mot sur la distance parcourue, mais indique combien de temps un objet a voyagé et à quelle vitesse. Vous pouvez ensuite calculer le déplacement en utilisant la durée et la vitesse.
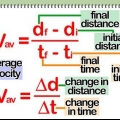
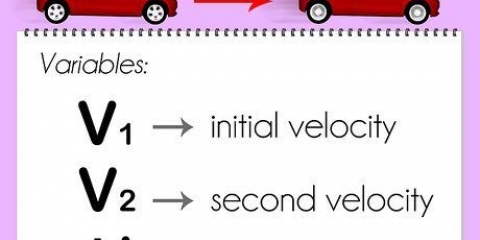
- Dans ce cas, l`équation ressemblera à ceci: s = 1/2(u + v)t.u = la vitesse initiale de l`objet, la vitesse à laquelle l`objet a commencé à se déplacer dans une direction particulière.v = la vitesse finale de l`objet, ou à quelle vitesse il est allé à la fin. t = le temps qu`il a fallu à l`objet pour atteindre sa destination.
- Par exemple : une voiture roule pendant 45 secondes.La voiture a tourné vers l`ouest avec une vitesse de 20 m/s (vitesse initiale) et au bout de la rue la vitesse est de 23 m/s (vitesse finale). Calcul du déplacement sur la base de ces données.

2. Entrez les valeurs pour la vitesse et le temps. Maintenant que vous savez depuis combien de temps la voiture roule et quelle était la vitesse de départ et d`arrivée, vous pouvez trouver la distance entre le point de départ et le point d`arrivée.

3. Établissez l`équation une fois que vous avez entré les valeurs. N`oubliez pas de calculer les termes dans le bon ordre sinon le déplacement se passera mal.
Partie 3 sur 5: Quand la vitesse, l`accélération et le temps sont donnés

1. Une autre équation est nécessaire si l`accélération est donnée pour un problème, ainsi que la vitesse et le temps. Avec une telle tâche, vous savez quelle a été la vitesse initiale de l`objet, quelle est l`accélération et combien de temps l`objet a été sur la route. Vous avez besoin de l`équation suivante.
- L`équation pour ce type de problème ressemble à ceci : s = ut + 1/2at².le "vous" représente toujours la vitesse initiale; le "une" est l`accélération de l`objet, ou aussi la vitesse à laquelle la vitesse de l`objet change. La variable"t" peut soit signifier le temps total, soit indiquer une période spécifique au cours de laquelle l`objet s`est accéléré. Quoi qu`il en soit, cela est indiqué en unités de temps telles que les secondes, les heures, etc.
- Supposons qu`une voiture avec une vitesse initiale de 25 m/s gagne une accélération de 3 m/s2 pendant une période de 4 secondes.Quelle est la cylindrée de la voiture après 4 secondes?

2. Remplissez les valeurs au bon endroit dans l`équation. Contrairement à l`équation précédente, seule la vitesse initiale est affichée ici, alors assurez-vous d`entrer les valeurs correctes.

3. Calculer le déplacement en résolvant l`équation. Un moyen rapide de vous aider à vous souvenir de l`ordre des opérations dans une équation est le mnémonique "M. Dale en attente de réponse".Indique toutes les opérations arithmétiques dans le bon ordre (exagération, multiplication, division, enracinement, addition et soustraction).
Partie 4 sur 5: Calcul du déplacement angulaire

1. Détermination du déplacement angulaire lorsqu`un objet se déplace le long d`une courbe. Bien que cela implique toujours de calculer le déplacement à l`aide d`une ligne droite, vous avez besoin de la différence entre la position de départ et la position de fin le long d`un chemin courbe.
- Prenons comme exemple une fille qui est sur un manège. Alors qu`elle tourne autour de l`extérieur de la roue, elle se déplace en cercle. Le déplacement angulaire essaie de trouver la distance la plus courte entre la position de départ et la position de fin si un objet ne se déplace pas en ligne droite.
- La formule du déplacement angulaire est : = S/r, par lequel "s" représente le déplacement linéaire, "r" pour le rayon, et "??" le déplacement angulaire est.Le déplacement linéaire est la distance parcourue par un objet le long d`un cercle.Le rayon est la distance d`un objet au centre du cercle.Le déplacement angulaire est la valeur que nous voulons connaître.

2. Branchez les valeurs du déplacement linéaire et du rayon dans l`équation. N`oubliez pas que le rayon est la distance entre le centre d`un cercle et le bord ; il se peut que le diamètre soit donné pour un problème, auquel cas vous devrez le diviser par 2 pour trouver le rayon (rayon) du cercle.

3. Diviser le déplacement linéaire par le rayon.Cela vous donnera le déplacement angulaire de l`objet.
Partie 5 sur 5: Comprendre le déplacement

1. Il est important de comprendre que "distance" signifie parfois autre chose que "déplacement."La distance dit quelque chose sur la distance totale qu`un objet s`est déplacée.
- La distance est quelque chose que nous appelons aussi un "scalaire" à mentionner. C`est un moyen d`indiquer la distance que vous avez parcourue, mais ne dit rien sur la direction dans laquelle vous vous êtes déplacé.
- Par exemple, si vous marchez 2 mètres à l`est, 2 mètres au sud, 2 mètres à l`ouest et encore 2 mètres au nord, vous êtes de retour à votre point de départ. Bien que vous ayez parcouru une distance totale de 10 mètres, votre déplacement est égal à 0 mètre, car votre point final est égal à votre point de départ.

2. Le déplacement est la différence entre deux points. Le déplacement n`est pas une somme de mouvements comme c`est le cas pour la distance ; il ne s`agit que de la partie entre votre point de départ et votre point d`arrivée.

3. Retiens bien les mots "d`avant en arrière" quand tu essaies d`imaginer un déplacement. La direction opposée annule le mouvement dans la direction d`origine.

4. Le déplacement est mesuré le long d`une ligne droite, pas le long d`un chemin circulaire. Pour connaître le mouvement, vous cherchez le chemin le plus court entre deux points différents.

5. Veuillez comprendre que le déplacement peut également avoir une valeur négative, contrairement à la distance. Si le point final est atteint en se déplaçant dans une direction opposée à la direction que vous avez commencée (par rapport au point de départ), alors votre déplacement est négatif.

6. Sachez que les valeurs de distance et de déplacement peuvent parfois être les mêmes. Si vous marchez tout droit sur 25 mètres puis vous vous arrêtez, la distance que vous avez parcourue est égale au déplacement, simplement parce que vous n`avez pas changé de direction.
Des astuces
- Travaillez avec précision
- Ne mémorisez pas les formules, mais essayez de comprendre comment elles fonctionnent
Nécessités
- Calculatrice
- Distancemètre
Articles sur le sujet "Calculer le déplacement"
Оцените, пожалуйста статью
Populaire