Déplacement = ré Le déplacement est la distance parcourue par un objet donné. Habituellement, l`unité de déplacement est notée en mètres. Temps = t Vitesse = v La vitesse vectorielle est la vitesse d`un objet dans une direction particulière. Lors du calcul de la vitesse instantanée, nous recherchons la vitesse d`un objet à un instant donné t (temps). La vitesse est généralement notée en mètres par seconde (m/s). Pente (ou "pente") = m Ici, il peut être utile de montrer le mouvement d`un objet dans un simple graphique x-y avec le temps tracé le long de l`axe des x et le déplacement le long de l`axe des y. Alors la pente de la ligne à un certain point est la vitesse de l`objet. 
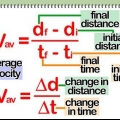
La vitesse (v) à un instant donné (t) est égale à la pente (taux de variation) de l`équation ci-dessus, où le déplacement (d) est tracé en fonction du temps (t). 
Une règle générale pour trouver la dérivée : Si y = a*x, alors la dérivée est a*n*x. Cette règle s`applique à tout terme du polynôme. La constante (le nombre sans variable à côté) disparaîtra car elle est multipliée par 0. 






Afin de calculer la vitesse instantanée, il est nécessaire de calculer la pente d`un graphique pour un point donné. 




La valeur à laquelle la pente se déplace lorsque H s`approche de 0 est la limite. C`est égal à la pente de la tangente à la courbe. La tangente est une droite définie comme une parallèle à la parabole sur une distance infiniment courte. La pente de la tangente est donc la pente de la parabole/courbe si H devient une distance infinitésimale sur la droite. L`équation pour trouver la tangente est la dérivée de l`équation de la fonction de déplacement, comme dans la première partie. 
Calculer la vitesse instantanée
Teneur
La vitesse vectorielle (velocity en anglais) est définie comme la vitesse d`un objet dans une direction particulière. À des fins générales, trouver la vitesse d`un objet est aussi simple que de diviser la distance parcourue par le temps qu`il faut pour parcourir cette distance. Mais cela ne donne que la vitesse moyenne le long d`un chemin donné. En utilisant des équations mathématiques et des dérivées, il est possible de calculer la vitesse de l`objet à un moment donné le long du chemin. C`est appelé Vitesse instantanée. Pour des raisons de commodité et de lisibilité, nous ferons référence à la vitesse dans ce qui suit, à la fois lorsque nous entendons la vitesse « normale » et la vitesse vectorielle.
Pas
Méthode 1 sur 2: Calcul de la vitesse instantanée

1. Qu`est-ce que "Vitesse instantanée". Les objets qui bougent peuvent le faire avec un vitesse constante – qui se déplace à vitesse constante tout au long du trajet. Un coureur qui court le long d`un terrain de football maintient à peu près la même vitesse sur toute la longueur du terrain. Les objets peuvent également se déplacer avec un vitesse variable. Par exemple, une voiture roulant sur une route avec de nombreux virages n`aura pas toujours la même vitesse - dans les virages, la vitesse diminue, pour augmenter à nouveau dans les lignes droites.
- Vitesse instantanée est une mesure de la vitesse d`un objet à un moment donné. Par exemple, la vitesse instantanée d`une fusée, exactement une seconde après l`allumage de l`ergol, est bien inférieure à sa vitesse instantanée 30 secondes après le décollage, si la fusée a eu le temps de prendre de la vitesse.

2. Connaissez vos variables. Lorsque vous traitez des calculs de vitesse instantanée, vous rencontrerez presque toujours certaines variables à un moment donné. Ces variables sont :

3. Un exemple. Disons que le déplacement d`un objet peut être représenté par une équation : déplacement(s) = 3t + 4t + 7. Le graphique de cette fonction est une ligne courbe ou une parabole, où l`axe des x représente le temps et l`axe des y représente le déplacement.

4. Pour calculer la vitesse instantanée d`un objet avec un déplacement selon la fonction ci-dessus, nous avons besoin de la dérivée de cette fonction. La dérivée d`une fonction est égale à la pente de la fonction en tout point du graphique. Pour trouver la dérivée, on différencie la fonction selon cette formule :

5. Utilisez cette formule pour calculer la dérivée de la fonction. Si nous notons cela comme y = 3x + 4x + 7, alors la dérivée est (3*2)*x+(4*1)*x+(7*0)*x

6. Simplifier l`équation. En multipliant tous les termes entre parenthèses, on obtient 6x+ 4x+ 0x

sept. Continuez à simplifier. Cette équation peut s`écrire 6x + 4. le "0x" terme devient alors égal à 0, tandis que le "4x" terme est simplifié à 4 (n = 1.)

8. Rendre cette nouvelle fonction égale à la pente m. Nous utilisons cette fonction dérivée pour trouver la pente de l`équation d`origine y = 3x + 4x + 7 pour toute valeur donnée de x (temps). La pente d`origine de l`équation à un instant donné est la vitesse instantanée.

9. Trouver la vitesse instantanée de l`objet pendant t=4 secondes. Tout ce que vous avez à faire est d`entrer la valeur du temps dans la variable x de la dérivée de l`équation. Cela donne l`équation suivante y = 6(4) + 4 . Ceci est simplifié à 28. La vitesse instantanée de l`objet pendant t=4 secondes est 28 m/s.
Méthode 2 sur 2: Comprendre un dérivé

1. Dessiner un système de coordonnées x-y ordinaire. Pour bien comprendre comment une dérivée peut aider à trouver la vitesse instantanée d`un objet, une représentation graphique est très utile. L`axe des y représente le déplacement de l`objet, tandis que l`axe des x représente le temps.
- Le graphique peut continuer sous l`axe des x. Si la ligne représentant le mouvement de l`objet descend en dessous de l`axe des x, cela signifie que l`objet se déplace dans le sens inverse et avant le point de départ. Habituellement, le graphique ne s`étendra pas au-delà de l`axe des y. La vitesse n`est pas mesurée pour les objets remontant dans le temps!
- Si vous ne savez pas comment tracer un graphique ou ce que représentent exactement l`axe des x et l`axe des y, apprenez à peut tracer le graphique d`une fonction.

2. Tracez une ligne courbe, en partant du point sur la ligne x=0, dans la direction de l`axe des x. La pente de la droite est la vitesse à laquelle y change divisé par la vitesse à laquelle x change. Donc, si y est égal au déplacement et x est égal au temps, alors la pente est égale à la vitesse.

3. Pour trouver la pente d`une droite pour un certain point, nous utilisons une astuce où nous trouvons la limite de l`équation. Trouver la limite nécessite deux points P et Q sur une ligne courbe et trouver la pente de la ligne à travers les deux points à mesure que la distance entre les deux points devient de plus en plus petite.

4. Choisissez un point P sur la ligne. Par exemple, placez P sur x=1. L`emplacement exact n`a pas d`importance. Choisissez une valeur qui vous convient.

5. Choisissez un deuxième point Q sur la ligne. Q doit être à une courte distance du P. Dans notre exemple, Q est au point avec x=3, tandis que P est au point avec x=1.

6. Trouver la pente entre P et Q. La pente entre P et Q devient alors (la différence de valeur y de P et Q)/(la différence de valeur x P et Q). Nous appelons cette différence des valeurs x de P et Q H. Dans ce cas H est égal à 3-1=2.

sept. Rendre la valeur de H plus petite. En d`autres termes, rapprochez Q de P sur l`axe des x, puis recalculez la pente entre P et Q. Faites-le à plusieurs reprises, en diminuant à chaque fois la distance entre P et Q. Après avoir calculé cela plusieurs fois, il devrait devenir clair que la pente approche d`une certaine valeur. Tant que H>0 la pente n`atteindra jamais cette valeur, mais s`approchera seulement. On dit alors que la pente la limite approche.

8. Utilisez des dérivées pour trouver la pente si H représente un intervalle infinitésimal sur la ligne. La dérivée d`une équation est trouvée par "x, est N*x" appliquer à n`importe quel terme de l`équation d`origine.
Des astuces
- Le déplacement est comme la distance, mais dans une certaine direction, donc le déplacement est un vecteur et la vitesse est une quantité scalaire. Le déplacement peut être négatif alors que la distance ne peut être que positive.
- Pour trouver l`accélération (le changement de vitesse au fil du temps), utilisez la méthode de la première partie pour trouver la dérivée de votre fonction de déplacement. Prenons alors la dérivée de celle. Cela vous donne ensuite l`équation pour trouver l`accélération à un moment donné - tout ce que vous avez à faire est d`entrer la valeur du temps dans cette dérivée seconde.
- L`équation reliant y (déplacement) à x (temps) peut être très simple, comme par exemple. y= 6x + 3. Dans ce cas la pente est constante et il n`est pas nécessaire de trouver une dérivée de la pente. Il est égal à 6, selon l`équation linéaire y = mx + b.
Articles sur le sujet "Calculer la vitesse instantanée"
Оцените, пожалуйста статью
Populaire