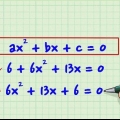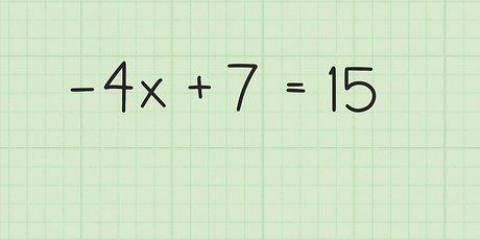Puisque 3x a un nombre fini de facteurs possibles, 3x et x, vous pouvez les écrire entre parenthèses : (3x +/- ? )(x +/-- ?) = 0. Ensuite, utilisez une méthode d`élimination où vous utilisez les facteurs de 4 pour trouver une combinaison qui donne -11x comme résultat de la multiplication. Vous pouvez utiliser soit une combinaison de 4 et 1, soit 2 et 2, car la multiplication des deux combinaisons de nombres produit 4. Gardez à l`esprit que l`un des termes doit être négatif, car le terme est -4. Essayez (3x +1)(x -4). Lorsque vous résolvez cela, vous obtenez - 3x -12x +x -4. Si vous combinez les termes -12x et x vous obtenez -11x, qui est le terme moyen auquel vous vouliez arriver. Maintenant que vous avez factorisé cette équation quadratique. Un autre exemple; on essaie de factoriser une équation qui ne marche pas : (3x-2)(x+2) = 3x +6x -2x -4. Si vous combinez ces termes, vous obtenez 3x -4x -4. Même si le produit de -2 et 2 est égal à -4, le moyen terme ne fonctionne pas car vous cherchiez -11x, pas -4x. 

3x + 1 = 0 = 3x = -1 = 3x/3 = -1/3 x = -1/3 x - 4 = 0 x = 4 x = (-1/3, 4) 

Ainsi, les deux solutions fonctionnent séparément et les deux sont vérifiées comme fonctionnant et sont correctes dans deux solutions différentes. 



{-b +/-√ (b - 4ac)}/2 {-(-5) +/-√ ((-5) - 4(3)(-8))}/2(3) = {-(-5) +/-√ ((-5) - (-96))}/2(3) 
{-(-5) +/-√ ((-5) - (-96))}/2(3) = {5 +/-√(25 + 96)}/6 {5 +/-√(121)}/6 

(5 + 11)/6 (5 - 11)/6 
(5 + 11)/6 = 16/6 (5-11)/6 = -6/6 
16/6 = 8/3 -6/6 = -1 x = (-1, 8/3) 

2x - 12x - 9 = 0 2x - 12x = 9 
2x/2 - 12x/2 = 9/2 = x - 6x = 9/2 
-6/2 = -3 = (-3) = 9 = x - 6x + 9 = 9/2 + 9 


x = 3 +(√6)/2 x = 3 - (√6)/2)
Résoudre des équations quadratiques
Teneur
Une équation quadratique est une équation où le plus grand exposant d`une variable est deux. Trois des méthodes les plus couramment utilisées pour résoudre ces équations sont : la factorisation, l`utilisation de la formule abc ou la division du carré. Si vous voulez savoir comment maîtriser ces méthodes, suivez simplement ces étapes.
Pas
Méthode 1 sur 3: Affacturage

1. Déplacer tous les termes d`un côté de l`équation. La première étape de la factorisation consiste à déplacer tous les termes d`un côté de l`équation, en laissant x positif. Appliquer l`opération d`addition ou de soustraction aux termes x, à la variable x et aux constantes, en les déplaçant ainsi d`un côté de l`équation, en ne laissant rien de l`autre côté. Voici comment cela fonctionne :
- 2x - 8x - 4 = 3x - x =
- 2x +x - 8x -3x - 4 = 0
- 3x - 11x = 0

2. Factoriser l`expression. Pour factoriser l`expression, vous devez factoriser les facteurs de 3x et les facteurs de la constante -4, les multiplier, puis les additionner pour donner la valeur du moyen terme, -11. Voici comment procéder :

3. Déterminer que chaque paire de parenthèses est égale à zéro et les traiter comme des équations séparées. Cela vous amène à trouver deux valeurs pour x qui rendent toutes les deux l`équation entière égale à zéro. Maintenant que vous avez factorisé l`équation, il ne vous reste plus qu`à rendre chaque paire de parenthèses égale à zéro. Donc tu peux écrire ça : 3x +1 = 0 et x - 4 = 0.

4. Résoudre chaque équation. Dans une équation quadratique, il y a deux valeurs données pour x. Résoudre chaque équation séparément en isolant la variable et écrire les résultats de x. Voici comment ça se passe :

5. Vérifier x = -1/3 po (3x + 1)(x – 4) = 0 :
On a (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... en substituant :(-1 + 1)(-4 1/3) ?=? 0 ..... en simplifiant :(0)(-4 1/3) = 0 ..... en multipliant : donc 0=0 ..... Oui, x = -1/3 fonctionne
On a (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... en substituant :(-1 + 1)(-4 1/3) ?=? 0 ..... en simplifiant :(0)(-4 1/3) = 0 ..... en multipliant : donc 0=0 ..... Oui, x = -1/3 fonctionne

6. Cochez x = 4 po (3x + 1)(x - 4) = 0 :
On obtient (3[4] + 1)([4] – 4) ?=? 0..... en substituant :(13)(4 – 4) ?=? 0 ..... par gradation :(13)(0) = 0 ..... en multipliant : 0=0 ..... Oui, x = 4 œuvres
On obtient (3[4] + 1)([4] – 4) ?=? 0..... en substituant :(13)(4 – 4) ?=? 0 ..... par gradation :(13)(0) = 0 ..... en multipliant : 0=0 ..... Oui, x = 4 œuvres
Méthode 2 sur 3: Application de la formule Abc

1. Déplacez tous les termes d`un côté de l`équation et fusionnez les termes similaires. Déplacez tous les termes d`un côté du signe égal, en gardant le terme x positif. Écrivez les termes par ordre de grandeur décroissant, donc x vient en premier suivi de x, puis de la constante. Voici comment procéder :
- 4x - 5x - 13 =x -5
- 4x - x - 5x - 13 +5 = 0
- 3x - 5x - 8 = 0

2. Écrivez la formule abc. C`est: {-b +/-√ (b - 4ac)}/2a

3. Déterminer les valeurs de a, b et c dans l`équation quadratique. La variable une est le coefficient de x, b est le coefficient de x et c est la constante. Pour l`équation 3x -5x - 8 = 0, a = 3, b = -5 et c = -8. Notez ceci.

4. Substituer les valeurs de a, b et c dans l`équation. Maintenant que vous connaissez les valeurs des trois variables, vous pouvez simplement les insérer dans l`équation comme nous le montrons ici :

5. Calculer. Après avoir rempli les chiffres, vous approfondissez le problème. Ci-dessous, vous pouvez lire comment cela va plus loin:

6. Simplifier la racine carrée. Si le nombre sous le signe radical est un carré parfait ou aussi un nombre carré, alors vous obtenez un nombre entier avec la racine carrée. Dans les autres cas, simplifiez au maximum la racine carrée. Si le nombre est négatif et que vous êtes sûr que c`est l`intention, alors la racine carrée du nombre sera moins simple. Dans cet exemple, (121) = 11. Vous pouvez alors écrire que x =(5 +/- 11)/6.

sept. Résoudre les nombres positifs et négatifs. Une fois que vous vous êtes débarrassé de la racine carrée, vous pouvez continuer jusqu`à ce que vous trouviez les réponses négatives et positives pour x. Maintenant que vous avez (5 +/- 11)/6, vous pouvez noter les deux possibilités :

8. Résoudre les réponses positives et négatives. Calculez plus loin :

9. Simplifier. Pour simplifier, divisez les réponses par le plus grand nombre divisible par le numérateur et le dénominateur. Divisez donc la première fraction par 2 et la seconde par 6 et vous avez résolu x.
Méthode 3 sur 3: Fractionner le carré

1. Déplacer tous les termes d`un côté de l`équation. Assurez-vous que le une de x est positif. Voici comment procéder :
- 2x - 9 = 12x =
- 2x - 12x - 9 = 0
- Dans cette équation, une égal à 2, b est de -12, et c est -9.

2. Déplacer la constante c de l`autre côté. La constante est la valeur numérique sans variable. Déplacez-le vers la droite de l`équation :

3. Divisez les deux côtés par le coefficient de la une ou x terme. Si x n`a pas de terme devant lui et a un coefficient avec la valeur 1, vous pouvez sauter cette étape. Dans ce cas, vous devez diviser tous les termes par 2, comme ceci :

4. Partie b par deux, carré et additionner les résultats des deux côtés du signe is.leb dans cet exemple est -6. Voici comment procéder :

5. Simplifier les deux côtés. Factorisez les termes de gauche pour obtenir (x-3)(x-3) ou (x-3). Ajoutez les termes à droite pour obtenir 9/2 + 9, ou 9/2 + 18/2, ce qui fait 27/2.

6. Trouver la racine carrée des deux côtés. La racine carrée de (x-3) est simplement (x-3). Vous pouvez également écrire la racine carrée de 27/2 sous la forme ±√(27/2). Par conséquent, x - 3 = ±√(27/2).

sept. Simplifier la racine carrée et résoudre pour x. Pour simplifier ±√(27/2), cherchez un carré parfait ou un nombre carré avec les nombres 27 ou 2 ou dans leurs facteurs. Le carré numéro 9 se trouve dans 27, car 9 x 3 = 27. Pour éliminer 9 de la racine, écrivez-le comme une racine séparée et simplifiez-vous en 3, la racine carrée de 9. Laissez √3 dans le numérateur de la fraction car il ne peut pas être séparé en tant que facteur de 27, et faites de 2 le dénominateur. Déplacez ensuite la constante 3 du côté gauche de l`équation vers le côté droit et notez vos deux solutions pour x :
Des astuces
- Comme vous pouvez le voir, le signe radical n`a pas complètement disparu. Par conséquent, les termes du numérateur ne sont pas fusionnés (ce ne sont pas des termes égaux). Donc inutile de diviser les moins et les plus. Au lieu de cela, en divisant, nous nous assurons que chaque facteur commun disparaît - mais "SEUL" si le facteur est égal pour les deux constantes, "ET" le coefficient de la racine carrée.
Articles sur le sujet "Résoudre des équations quadratiques"
Оцените, пожалуйста статью
Populaire