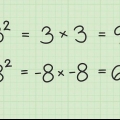Si le mouvement vous amène à une "boîte" au-dessus du carré magique, restez dans la colonne de cette boîte, mais placez le nombre dans la rangée du bas de cette colonne. Si le mouvement vous amène à une case à droite du carré magique, restez dans cette rangée, mais placez le nombre dans la colonne de cette rangée, à l`extrême gauche du carré. Si le coup vous amène à une case qui a déjà un numéro, revenez à la case précédente qui a été remplie et placez le numéro suivant directement au-dessus. 

somme = [6 * (62 + 1)] / 2 somme = [6 * (36 + 1)] / 2 somme = (6 * 37) / 2 somme = 222 / 2 La constante magique d`un carré 6x6 est 222/2, soit 111. Toutes les lignes, colonnes et diagonales doivent être additionnées pour obtenir ce nombre. 
Ainsi, pour chaque carré 6x6, chaque quadrant devient un carré 3x3. 
Dans l`exemple d`un carré 6x6, le quadrant A est résolu avec les nombres de 1 à 9 ; Quadrant B avec ceux de 10-18 ; Quadrant C avec 19-27 et quadrant D avec 28-36. 
Traitez le premier nombre de chaque quadrant comme s`il s`agissait d`un un. Placez-le dans la case du milieu sur la rangée supérieure de chaque quadrant. Traitez chaque quadrant comme un petit carré magique. Même si la case est disponible dans un quadrant adjacent, ignorez-la et passez à la "règle d`exception" qui correspond à cette situation. 
Utilisez un crayon pour marquer tous les carrés de la rangée supérieure jusqu`à ce que vous atteigniez la case du milieu du quadrant A. Ainsi, dans un carré 6x6, vous cochez la case 1 (avec le numéro 8), mais dans un carré 10x10, vous cochez les cases 1 et 2 (avec les numéros 17 et 24, respectivement). Marquez un carré en utilisant les cases que vous venez de marquer comme rangée du haut. Si vous n`avez coché qu`une seule case, votre carré ne comportera pas plus d`une case. Nous appelons cela le marquage A-1. Ainsi, dans un carré magique 10x10, le marqueur A-1 est composé des cases 1 et 2 des rangées 1 et 2, créant un carré 2x2 dans le quadrant supérieur gauche. Dans la rangée immédiatement en dessous du marqueur A-1, sautez le numéro de la première colonne, puis cochez autant de cases d`un côté à l`autre que vous avez indiqué au marqueur A-1. Nous appelons cette rangée du milieu Marquage A-2. La sélection A-3 est une case similaire à A-1, mais placée dans le coin inférieur gauche du quadrant. Les sélections A-1, A-2 et A-3 forment ensemble le marqueur A. Répétez ce processus dans le quadrant D, en créant une zone de marqueur identique, Marker D. 

Voici deux images d`un carré magique 14x14 avant et après les deux commutateurs. La surface de commutation du quadrant A est marquée en bleu, la surface du quadrant D est verte, celle du quadrant C jaune et celle du quadrant B orange. Carré magique de 14x14 avant le basculement (étapes 6, 7 et 8) Carré magique de 14x14 après avoir effectué les substitutions (étapes 6, 7 et 8) 

somme = [4 * (42 + 1)] / 2 somme = [4 * (16 + 1)] / 2 somme = (4 * 17) / 2 somme = 68 / 2 La constante magique d`un carré 4x4 est 68/2, soit 34. Toutes les lignes, colonnes et diagonales doivent former ce nombre. 
Dans un carré 4x4, il suffit de marquer les quatre carrés d`angle. Dans un carré 8x8, chaque marqueur est une zone 2x2 dans les coins. Dans un carré de 12x12, chaque marqueur est une zone de 3x3 dans les coins, etc. 
Dans un carré 4x4, le marqueur central est une zone 2x2 au centre. Dans un carré 8x8, le marqueur central est une zone 4x4 au centre, etc. 
1 dans la case en haut à gauche et 4 dans la case en haut à droite 6 et 7 dans les cases du milieu de la rangée 2 10 et 11 dans les cases du milieu de la rangée 3 13 dans la case en bas à gauche et 16 dans la case en bas à droite. 
15 et 14 dans les cases du milieu de la rangée 1 12 dans la case la plus à gauche et 9 dans la case la plus à droite de la rangée 2 8 dans la case la plus à gauche et 5 dans la case la plus à droite de la rangée 3 3 et 2 dans les cases du milieu de la rangée 4 À ce stade, toutes les colonnes, lignes et diagonales doivent avoir une somme égale à la constante magique précédemment calculée.
Résoudre des carrés magiques
Teneur
Les carrés magiques n`ont gagné en popularité que depuis l`essor des jeux basés sur les mathématiques comme le Sudoku. Un carré magique est un arrangement de nombres dans un carré de telle sorte que la somme de chaque ligne, colonne et diagonale soit un nombre constant, la constante magique. Cet article va expliquer comment résoudre tout type de carré magique, qu`il s`agisse d`un carré impair, pair simple ou double pair.
Pas
Méthode 1 sur 3: Résoudre un carré magique impair

1. Calculer la constante magique. Vous pouvez trouver ce nombre à l`aide d`une formule mathématique simple, où n = le nombre de lignes ou de colonnes de votre carré magique. Ainsi, par exemple, dans un carré magique 3x3, n = 3. La constante magique = [n * (n2 + 1)] / 2. Donc dans l`exemple du carré 3x3 :
- somme = [3 * (32 + 1)] / 2
- somme = [3 * (9 + 1)] / 2
- somme = (3 * 10) / 2
- somme = 30 / 2
- La constante magique d`un carré 3x3 est 30/2, soit 15.
- Toutes les lignes, colonnes et diagonales ont ce nombre comme somme.

2. Placez le numéro 1 dans la case du milieu de la rangée du haut. C`est toujours le point de départ si votre carré magique de côtés a un nombre impair de côtés, peu importe la taille de ce nombre. Donc, si vous avez un carré 3x3, mettez le chiffre 1 dans la case 2 ; dans un carré de 15x15, placez le chiffre 1 dans la case 8.

3. Remplissez les nombres restants dans un modèle un-à-droite. Vous remplissez toujours les nombres selon une série (1, 2, 3, 4, etc.) en remontant d`une ligne puis d`une colonne vers la droite. Vous remarquez tout de suite que pour placer le chiffre 2 vous vous retrouvez au dessus de la rangée du haut, en dehors du carré magique. Ce n`est pas grave, bien que vous utilisiez toujours la méthode un par un, un à droite, il existe trois exceptions qui suivent également un modèle prévisible :
Méthode 2 sur 3: Résoudre un simple carré magique pair

1. Comprendre ce qu`est un simple carré pair. Tout le monde sait qu`un nombre pair est divisible par 2, mais avec les carrés magiques, il existe différentes méthodes pour résoudre les carrés pairs simples et doubles.
- Un simple carré pair a un nombre de carrés par côté qui est divisible par 2, mais pas par 4.
- Le plus petit carré magique pair est 6x6, car les carrés magiques 2x2 ne peuvent pas être créés.

2. Calculer la constante magique. Utilisez la même méthode que pour les carrés magiques impairs : la constante magique = [n * (n2 + 1)] / 2, où n = le nombre de carrés par côté. Donc, dans l`exemple d`un carré 6x6 :

3. Divisez le carré magique en quatre quadrants de taille égale . Étiquetez-les A (en haut à gauche), C (en haut à droite), D (en bas à gauche) et B (en bas à droite). Pour déterminer la taille de chaque carré, divisez par deux le nombre de cases dans chaque ligne ou colonne.

4. Attribuez une plage de nombres à chaque quadrant. Le quadrant A obtient un quart des nombres ; Quadrant B le deuxième trimestre ; Quadrant C le troisième quart et Quadrant D le dernier quart de la plage de nombres totale d`un carré magique 6x6.

5. Résoudre chaque quadrant en utilisant la méthode du carré magique avec un nombre impair de cases par côté. Le quadrant A est facile à remplir car il commence par le chiffre 1, comme le font généralement les carrés magiques. Les quadrants B-D, cependant, commencent par des nombres impairs - 10, 19 et 28, comme pour notre exemple.

6. Faire les marqueurs A et D. Si vous avez essayé d`ajouter des colonnes, des lignes et des diagonales tout de suite, vous avez remarqué qu`ils ne correspondent pas à la constante magique. Vous devrez permuter certaines cases des quadrants supérieur gauche et inférieur gauche pour compléter votre carré magique. Nous appelons ces zones Marker A et Marker D.

sept. Échanger les marqueurs A et D. Il s`agit d`un échange 1 à 1. Déplacez les cases entre le quadrant A et le quadrant D sans changer l`ordre. Une fois que vous avez fait cela, toutes les lignes, colonnes et diagonales de votre carré magique devraient avoir la constante magique précédemment calculée comme somme.

8. Échangez une fois de plus contre des carrés magiques individuels, même plus grands que 6x6. En plus du basculement pour les Quadrants A et D mentionné ci-dessus, vous devez également effectuer un basculement pour les Quadrants C et B. Marquez les colonnes du côté droit du carré vers la gauche, une de moins que le nombre de colonnes marquées pour le surlignage A-1. Échangez les valeurs du quadrant C avec les valeurs du quadrant B pour ces colonnes, en utilisant la même méthode un-à-un.
Méthode 3 sur 3: Résoudre un double carré magique pair

1. Comprendre ce qu`est un double carré pair. Un carré pair simple a un nombre de carrés par côté qui est divisible par 2. Un double carré pair a un nombre de carrés par côté qui sont divisibles par 4.
- Le plus petit carré doublement régulier que l`on puisse faire est le carré 4x4.

2. Calculer la constante magique. Utilisez la même méthode que pour les carrés magiques pairs impairs ou singuliers : la constante magique = [n * (n2 + 1)] / 2, où n = le nombre de carrés par côté. Ainsi, dans l`exemple d`un carré 4x4 :

3. Appliquer les marqueurs A-D. Dans chaque coin du carré magique, placez un petit carré avec des côtés de n/4, où n = la longueur d`un côté du carré magique entier. Dans le sens inverse des aiguilles d`une montre, étiquetez-les en tant que marqueurs A, B, C et D.

4. Placer la marque centrale. Marquez toutes les cases au centre du carré magique dans une zone carrée de longueur n/2, où n = la longueur de chaque côté d`un carré magique complet. Le marqueur central ne doit pas chevaucher les marqueurs A-D, mais doit les toucher dans les coins.

5. Remplissez le carré magique, mais uniquement dans les zones marquées. Commencez à remplir vos nombres de carrés magiques de gauche à droite, mais ne placez un nombre que si la case se trouve dans un marqueur. Ainsi, dans une case 4x4, remplissez les cases suivantes :

6. Remplissez le reste du carré magique en comptant à rebours. C`est essentiellement l`inverse de l`étape précédente. Recommencez avec la case en haut à gauche, mais cette fois ignorez toutes les cases qui tombent dans la zone marquée, et remplissez les cases non sélectionnées en comptant à rebours. Commencez par le plus grand nombre de votre plage de nombres. Ainsi, dans un carré magique 4x4, remplissez :
Des astuces
- Essayez des variantes de ces étapes pour découvrir vos propres méthodes de solution.
Nécessités
- Crayon
- Papier
- La gomme
Articles sur le sujet "Résoudre des carrés magiques"
Оцените, пожалуйста статью
Similaire
Populaire