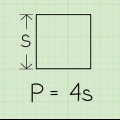
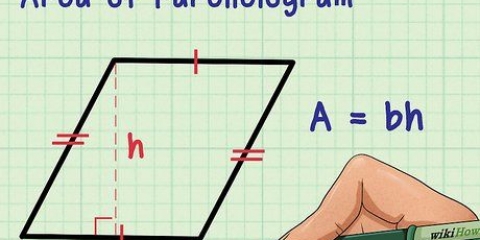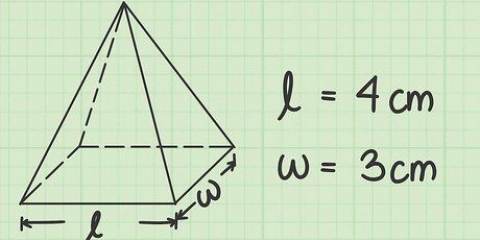Puisque les quatre côtés d`un carré sont égaux, la « longueur » du carré sera identique à sa « largeur ». Dans ce cas, vous n`avez besoin de mesurer que dans un sens. 
Par exemple, supposons que vous ayez une zone rectangulaire d`une longueur de 4 centimètres et d`une largeur de 3 centimètres. Dans ce cas l`aire du rectangle est de 4 × 3=12 centimètres carrés. Dans le cas des carrés, étant donné que les quatre côtés sont les mêmes, vous pouvez simplement mesurer un côté et le multiplier par lui-même (également appelé « quadrillage » ou élever la puissance à la seconde puissance) pour calculer l`aire en centimètres carrés. 

Donc, si vous avez une base d`une longueur de 4 centimètres et que la hauteur correspondante est de 3 centimètres, alors votre résultat sera 2 x 3 = 6 centimètres carrés. 
Donc, si la longueur d`un côté est de 5 centimètres et la hauteur est de 4 centimètres, alors la surface résultante est de 5 x 4 = 20 centimètres. 
Ainsi, si le côté long de votre trapèze mesure 6 centimètres, le côté court fait 4 centimètres et la hauteur est de 5 centimètres, le résultat sera ½ x 5 x (6 + 4) = 25 cm. 
Donc, si vous avez un hexagone avec 6 côtés égaux de 4 centimètres chacun (ce qui signifie P=6 x 4=24) et un apothème de 3,5 centimètres, alors le calcul est ½ x 24 x 3,5=42 cm. 
Donc, si vous avez un octogone régulier d`une longueur de 4 centimètres, vous calculez (2 x16) x (1 + 1,4) = 32 x 2,4 = 76,8 cm. 

Par exemple 400 pieds carrés=400 x 144=57600 pouces. 
De même, 1 mètre carré est égal à 10.000 centimètres carrés, et qu`un kilomètre carré est égal à 10.000.000.000 centimètres carrés. Donc un kilomètre carré = 10.000.000.000 centimètres carrés x 0,155=1.550.003.100 pouces.
Calculer les centimètres carrés
Teneur
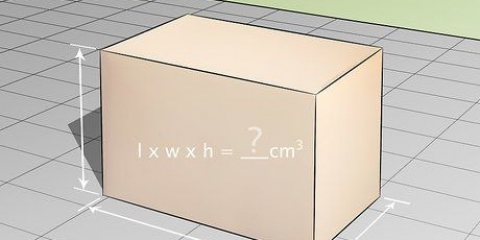
Déterminer le centimètre carré (également écrit en cm) dans un espace à deux dimensions est généralement assez simple. Dans les cas les plus simples, comme un carré ou un rectangle, l`aire en centimètres carrés peut être calculée à l`aide de l`équation longueur × largeur. La zone des autres formes (cercles, triangles, etc.) peut être calculé via un certain nombre d`équations mathématiques spécialisées. De plus, si nécessaire, vous pouvez facilement convertir en pouces carrés des pieds carrés ou des centimètres carrés.
Pas
Méthode 1 sur 3: Détermination des centimètres carrés dans un carré ou un rectangle

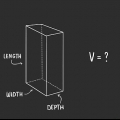
1. Particulier longueur de la surface à mesurer. Les carrés et les rectangles ont quatre côtés droits. Dans le cas des rectangles, les côtés opposés sont de même longueur tandis que dans le cas des carrés, les quatre côtés sont égaux. Mesurez l`un des côtés du carré ou le côté le plus long du rectangle pour la longueur.

2. Particulier largeur de la surface à mesurer. Ensuite, vous mesurez l`un des côtés adjacents au côté que vous venez de mesurer. Ce côté doit couper le premier côté à un angle de 90 degrés. Cette deuxième mesure est la largeur du carré ou du rectangle.

3. Multiplier la longueur × la largeur. Multipliez la longueur et la largeur de votre carré ou rectangle pour trouver la surface en centimètres carrés.
Méthode 2 sur 3: Détermination de la zone pour d`autres formes

1. Trouvez l`aire d`un cercle avec l`équation area=pi × r. Pour calculer l`aire d`un cercle en centimètres carrés, il suffit de connaître la distance du centre du cercle au bord en centimètres. Cette distance est appelée la Rayon du cercle. Une fois que vous connaissez cette valeur, remplacez-la par « r » dans l`équation ci-dessus. Multiplier le rayon par lui-même, puis par la constante mathématique pi (3.1415926...) pour déterminer le nombre de centimètres carrés à l`intérieur du cercle.
- Ainsi, un cercle de 4 centimètres de rayon a une aire de 50,27 centimètres carrés, le produit de 3,14 x 16.

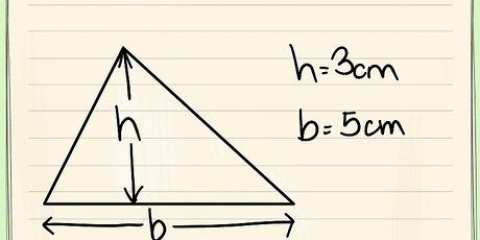
2. Trouvez l`aire d`un triangle à l`aide de l`équation Aire=1/2 b × h en centimètres carrés. L`aire d`un triangle s`obtient en multipliant la base (`b`) par la hauteur (`h`). La base d`un triangle est la longueur de l`un de ses côtés, tandis que sa hauteur est la distance de la "base" au coin opposé, mesurée à un angle de 90 degrés par rapport à la "base". L`aire d`un triangle peut être calculée en utilisant sa base et sa hauteur, pour chacun de ses trois côtés et l`angle opposé.

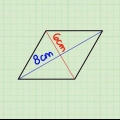
3. Trouvez l`aire d`un parallélogramme en utilisant l`équation Aire = b × h. Les parallélogrammes sont similaires aux rectangles ; la seule différence est que leurs angles ne sont pas nécessairement de 90 degrés. La façon de calculer l`aire en centimètres carrés d`un parallélogramme est similaire à la façon de calculer celle d`un rectangle - il suffit de multiplier la base d`un parallélogramme par sa hauteur, en s`assurant que les deux mesures sont en centimètres. La base est la longueur de l`un des côtés tandis que la hauteur est la distance de la base au côté opposé mesurée à angle droit.

4. Trouver l`aire d`un trapèze en utilisant l`équation Aire=1/2 × h × (B + b). Un trapèze est une forme quadrilatérale avec deux côtés parallèles et deux côtés non parallèles. Pour calculer l`aire en centimètres carrés, vous devez connaître trois mesures (en centimètres) : la longueur du côté parallèle le plus long (`B`), la longueur du côté parallèle le plus court (`b`) et la hauteur ( ` h`) du trapèze (la distance entre les deux côtés parallèles, mesurée à angle droit). Additionnez les longueurs des deux côtés ensemble, multipliez cela par la hauteur, puis divisez par deux le résultat pour trouver l`aire du trapèze.

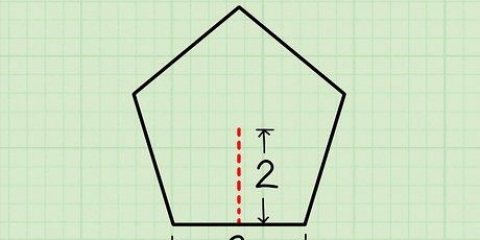
5. Trouvez l`aire d`un hexagone avec l`équation Aire=½ × P × a. Cette formule fonctionne pour n`importe quel hexagone régulier, ce qui signifie qu`il a 6 côtés égaux et 6 angles égaux. p représente le périmètre ou 6 fois la longueur d`un côté (6 x s) pour un hexagone régulier. une représente l`apothème - la longueur du centre de l`hexagone au centre d`un côté (c`est-à-dire à mi-chemin entre 2 coins). Multipliez cela et divisez par deux le résultat pour trouver la zone.

6. Trouvez l`aire d`un octogone avec l`équation aire=2a² × (1 + √2). Pour un octogone régulier (avec 8 côtés égaux et 8 angles égaux), il suffit de connaître la longueur d`un côté ("a" dans la formule) pour calculer l`aire. Utilisez cette mesure dans la formule et vous avez votre résultat.
Méthode 3 sur 3: Conversions en pouces carrés

1. Convertissez les dimensions en pouces avant de faire des calculs. Pour obtenir votre réponse finale en pouces carrés, il est préférable d`avoir toutes les mesures nécessaires pour la formule (telles que la longueur, la hauteur ou l`apothème) en pouces. Donc, si les côtés de votre carré mesurent 1 pied chacun, convertissez-le en 12 pouces avant de calculer l`aire. Voici les facteurs de conversion pour les unités de mesure couramment utilisées :
- 1 pied = 12 pouces
- 1 mètre = 36 pouces
- 1 centimètre = 0,3937 pouce
- 1 mètre = 39,3701 pouces
- 1 millimètre = 0,0394 pouce

2. Multiplier par 144 pour convertir de pieds carrés en pouces carrés. 1 pied carré est littéralement 1 pied carré (ou 1 pied fois 1 pied); C`est la même chose que 12 pouces fois 12 pouces, ou 144 pouces carrés. Donc, si vous avez une superficie en pieds carrés, multipliez-la par 144 pour obtenir la superficie en pouces carrés.

3. Multipliez par 0,155 pour convertir des centimètres carrés en pouces carrés. 1 centimètre équivaut à environ 0,394 pouces et 0,394 au carré (0,394 x 0,394) i équivaut à 0,155. Donc, si vous devez convertir une surface de 250 cm en pouces, vous multipliez 250 par 0,155 et vous obtenez 38,75 pouces.
Articles sur le sujet "Calculer les centimètres carrés"
Оцените, пожалуйста статью
Populaire