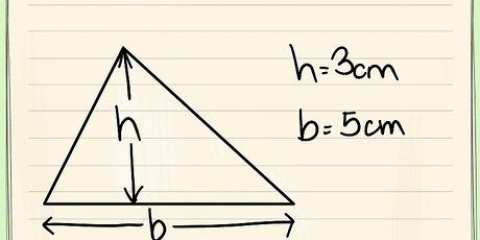
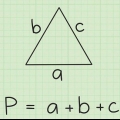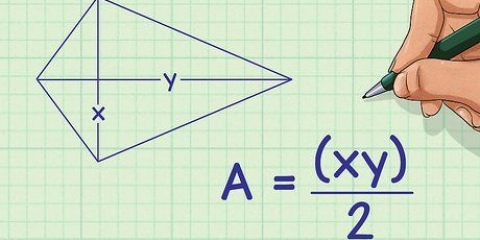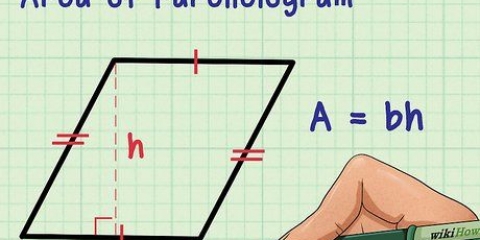Par exemple, si vous avez un trapèze avec un haut de 2 cm, un bas de 3 cm et deux côtés de 1 cm, votre formule ressemblerait à ceci :


Par exemple:


La circonférence du trapèze est donc de 7 cm. 

Par exemple, si vous avez un trapèze d`une hauteur de 6 cm, vous devez tracer une ligne de chaque sommet supérieur vers le bas. Remarque 6 cm pour chaque ligne. 
Par exemple, si le haut du trapèze mesure 6 cm, alors la partie médiane du bas mesure également 6 cm. 

Par exemple, si vous savez que la hauteur du trapèze est de 6 cm et la longueur du côté (hypoténuse) est de 9 cm, votre équation ressemblerait à ceci :


Par exemple : est l`équation  , puis tu carrés 6 et 9 et soustrais le carré de 6 du carré de 9 :
, puis tu carrés 6 et 9 et soustrais le carré de 6 du carré de 9 :




Par exemple:




Alors prenez note comme base du premier triangle.
comme base du premier triangle. 
Par exemple, si le deuxième côté du trapèze mesure 7 cm, calculez comme suit :





Alors prenez note comme base du deuxième triangle.
comme base du deuxième triangle. 
Par exemple: 
Après avoir converti les racines carrées en décimales, vous avez
Ainsi, la circonférence approximative de votre trapèze est de 38,314 cm.. 

Par exemple, si vous avez un trapèze d`une hauteur de 6 cm, tracez une ligne de chaque sommet supérieur vers le bas. Remarque 6 cm à chaque ligne. 
Par exemple, si le haut du trapèze mesure 6 cm, alors la partie médiane du bas mesure également 6 cm. 
Avec ce rapport, vous pouvez trouver la longueur de l`hypoténuse du triangle, qui est également le premier côté du trapèze. L`hypoténuse est le côté opposé à l`angle de 90 degrés d`un triangle rectangle. 
Supposons que l`angle intérieur donné soit de 35 degrés et que la hauteur du triangle soit de 6 cm, alors votre formule ressemblera à ceci :


Par exemple, en utilisant une calculatrice, vous constaterez que le sinus d`un angle de 35 degrés est de 0,5738 (arrondi). Donc ta formule est maintenant :


Par exemple:




Ainsi, la longueur de l`hypoténuse et du premier côté manquant du trapèze est d`environ 10,4566 cm. 
Par exemple, si l`angle intérieur donné est de 45 degrés, calculez :





Donc la longueur de l`hypoténuse et du deuxième côté manquant du trapèze est d`environ 8,4854 cm. 

Par exemple, si le premier triangle rectangle a une hypoténuse de 10,4566 et une hauteur de 6, votre formule est :


Par exemple:






Donc la base du triangle et la première partie manquante du bas du trapèze mesure environ 8,5639 cm. 
Par exemple, si le deuxième triangle rectangle a une hypoténuse de 8,4854 et une hauteur de 6, vous calculerez comme suit :






Donc la base du deuxième triangle, et la deuxième partie manquante du bas du trapèze, est égale à 6 cm. 
Par exemple: 
La circonférence approximative du trapèze est donc de 45,5059 cm.
Calculer le périmètre d'un trapèze
Teneur
Un trapèze est défini comme un quadrilatère avec deux côtés parallèles. Comme pour tout polygone, vous devez additionner les quatre côtés pour trouver le périmètre d`un trapèze (ou trapèze). Souvent, cependant, vous manquerez des longueurs de côté, mais vous avez d`autres données, telles que la hauteur du trapèze ou les mesures d`angle. En utilisant ces données, vous pouvez trouver les longueurs inconnues des côtés en utilisant les règles de la géométrie et de la trigonométrie.
Pas
Méthode 1 sur 3: Si vous connaissez la longueur des deux côtés et la base

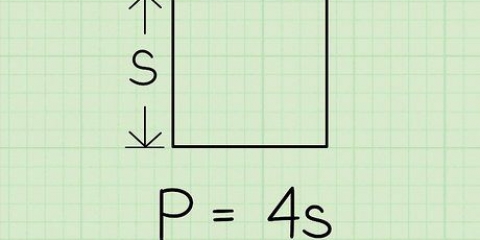
1. Définir la formule pour la circonférence d`un trapèze. La formule est  , par lequel
, par lequel  est égal au périmètre du trapèze, et la variable
est égal au périmètre du trapèze, et la variable  est égal à la longueur du sommet du trapèze,
est égal à la longueur du sommet du trapèze,  égale la longueur du bas,
égale la longueur du bas,  est égal à la longueur du côté gauche et
est égal à la longueur du côté gauche et  est égal à la longueur du côté droit.
est égal à la longueur du côté droit.
 , par lequel
, par lequel  est égal au périmètre du trapèze, et la variable
est égal au périmètre du trapèze, et la variable  est égal à la longueur du sommet du trapèze,
est égal à la longueur du sommet du trapèze,  égale la longueur du bas,
égale la longueur du bas,  est égal à la longueur du côté gauche et
est égal à la longueur du côté gauche et  est égal à la longueur du côté droit.
est égal à la longueur du côté droit.
2. Utilisez les longueurs de côté dans la formule. Si vous ne connaissez pas la longueur des quatre côtés du trapèze, vous ne pouvez pas utiliser cette formule.


3. Ajouter les longueurs de côté ensemble. Cela vous donnera la circonférence de votre trapèze.


La circonférence du trapèze est donc de 7 cm.
Méthode 2 sur 3: Si vous connaissez la hauteur, les deux longueurs latérales et la longueur supérieure

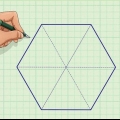
1. Divisez le trapèze en un rectangle et deux triangles rectangles. Pour ce faire, dessinez la hauteur des deux coins supérieurs.
- Si vous ne pouvez pas former les deux triangles rectangles car un côté du trapèze est perpendiculaire à la base, assurez-vous que ce côté a la même longueur que la hauteur et divisez le trapèze en un rectangle et un triangle rectangle.

2. Donner la longueur de chaque courbe de niveau. Puisque ce sont les côtés opposés d`un rectangle, ils auront la même longueur.

3. Notez la longueur de la partie médiane du bas. (C`est le bas du rectangle.) La longueur sera égale à la longueur du sommet (le sommet du rectangle), car les côtés opposés d`un rectangle ont la même longueur. Si vous ne connaissez pas la longueur du haut, vous ne pouvez pas utiliser cette méthode.

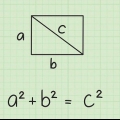
4. Mettre en place le théorème de Pythagore pour le premier triangle rectangle. La formule est  , par lequel
, par lequel  est la longueur de l`hypoténuse du triangle rectangle (le côté opposé à l`angle droit),
est la longueur de l`hypoténuse du triangle rectangle (le côté opposé à l`angle droit),  est la hauteur du triangle rectangle et
est la hauteur du triangle rectangle et  est la longueur de la base du triangle.
est la longueur de la base du triangle.
 , par lequel
, par lequel  est la longueur de l`hypoténuse du triangle rectangle (le côté opposé à l`angle droit),
est la longueur de l`hypoténuse du triangle rectangle (le côté opposé à l`angle droit),  est la hauteur du triangle rectangle et
est la hauteur du triangle rectangle et  est la longueur de la base du triangle.
est la longueur de la base du triangle.
5. Utilisez les valeurs connues du premier triangle dans la formule. Assurez-vous d`entrer la longueur du côté du trapèze pour  . Entrez la hauteur du trapèze pour
. Entrez la hauteur du trapèze pour  .
.
 . Entrez la hauteur du trapèze pour
. Entrez la hauteur du trapèze pour  .
.

6. Carré des valeurs connues dans l`équation. Soustrayez ensuite les valeurs au carré les unes des autres pour obtenir  isoler.
isoler.
 isoler.
isoler. , puis tu carrés 6 et 9 et soustrais le carré de 6 du carré de 9 :
, puis tu carrés 6 et 9 et soustrais le carré de 6 du carré de 9 :



sept. Prendre la racine carrée pour obtenir la valeur de b  trouver. (Pour des instructions complètes sur la simplification des racines carrées, lisez cet article sur le sujet). Le résultat vous donnera la valeur de la base manquante de votre premier triangle rectangle. Écris cette longueur à la base de ton triangle.
trouver. (Pour des instructions complètes sur la simplification des racines carrées, lisez cet article sur le sujet). Le résultat vous donnera la valeur de la base manquante de votre premier triangle rectangle. Écris cette longueur à la base de ton triangle.
 trouver. (Pour des instructions complètes sur la simplification des racines carrées, lisez cet article sur le sujet). Le résultat vous donnera la valeur de la base manquante de votre premier triangle rectangle. Écris cette longueur à la base de ton triangle.
trouver. (Pour des instructions complètes sur la simplification des racines carrées, lisez cet article sur le sujet). Le résultat vous donnera la valeur de la base manquante de votre premier triangle rectangle. Écris cette longueur à la base de ton triangle.



Alors prenez note
 comme base du premier triangle.
comme base du premier triangle.
8. Trouver la longueur manquante du deuxième triangle rectangle. Pour ce faire, mettez en place le théorème de Pythagore pour le deuxième triangle et suivez les étapes pour trouver la longueur du côté manquant. Si vous travaillez avec un trapèze isocèle (celui où les deux côtés non parallèles ont la même longueur), alors les deux triangles rectangles sont congrus, donc la valeur du premier triangle est égale à celle du deuxième triangle.





Alors prenez note
 comme base du deuxième triangle.
comme base du deuxième triangle.
9. Additionner toutes les longueurs de côté du trapèze. Le périmètre d`un polygone est la somme de tous ses côtés :  . Pour le bas, ajoutez le côté inférieur du rectangle, ainsi que les bases des deux triangles. Vous aurez probablement des racines carrées dans votre réponse. Pour des instructions complètes sur l`ajout de racines carrées, lisez l`article sur ce sujet. Vous pouvez également utiliser une calculatrice pour convertir les racines carrées en décimales.
. Pour le bas, ajoutez le côté inférieur du rectangle, ainsi que les bases des deux triangles. Vous aurez probablement des racines carrées dans votre réponse. Pour des instructions complètes sur l`ajout de racines carrées, lisez l`article sur ce sujet. Vous pouvez également utiliser une calculatrice pour convertir les racines carrées en décimales.
 . Pour le bas, ajoutez le côté inférieur du rectangle, ainsi que les bases des deux triangles. Vous aurez probablement des racines carrées dans votre réponse. Pour des instructions complètes sur l`ajout de racines carrées, lisez l`article sur ce sujet. Vous pouvez également utiliser une calculatrice pour convertir les racines carrées en décimales.
. Pour le bas, ajoutez le côté inférieur du rectangle, ainsi que les bases des deux triangles. Vous aurez probablement des racines carrées dans votre réponse. Pour des instructions complètes sur l`ajout de racines carrées, lisez l`article sur ce sujet. Vous pouvez également utiliser une calculatrice pour convertir les racines carrées en décimales.
Après avoir converti les racines carrées en décimales, vous avez

Ainsi, la circonférence approximative de votre trapèze est de 38,314 cm..
Méthode 3 sur 3: Si vous connaissez la hauteur, la longueur des coins intérieurs supérieur et inférieur

1. Divisez le trapèze en un rectangle et deux triangles rectangles. Pour cela, indiquez la hauteur à partir des deux coins supérieurs.
- Si vous ne pouvez pas former deux triangles rectangles parce qu`un côté du trapèze est perpendiculaire à la base, assurez-vous que ce côté est de la même taille que la hauteur et divisez le trapèze en un rectangle et un triangle rectangle.

2. Étiquetez chaque contour. Puisque ce sont les côtés opposés d`un rectangle, ils auront la même longueur.

3. Notez la longueur de la partie médiane du bas. (C`est le bas du rectangle.) Cette longueur sera égale à la longueur du sommet, car les côtés opposés d`un rectangle ont la même longueur.

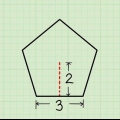
4. Mettre en place la formule du sinus pour le premier triangle rectangle. La formule est  , par lequel
, par lequel  le coin intérieur est,
le coin intérieur est,  la hauteur du triangle et
la hauteur du triangle et  est la longueur de l`hypoténuse.
est la longueur de l`hypoténuse.
 , par lequel
, par lequel  le coin intérieur est,
le coin intérieur est,  la hauteur du triangle et
la hauteur du triangle et  est la longueur de l`hypoténuse.
est la longueur de l`hypoténuse.
5. Utiliser les valeurs connues dans le rapport sinusoïdal. Assurez-vous d`utiliser la hauteur du triangle comme longueur du côté opposé dans la formule. vous résolvez cela pour H.


6. Déterminer le sinus de l`angle. Pour ce faire, utilisez le bouton SIN sur une calculatrice scientifique. Utiliser cette valeur dans la formule.


sept. Résoudre ceci pour H. Pour ce faire, multipliez chaque côté par H, puis divisez chaque côté par l`angle sinus. Ou diviser la hauteur du triangle par l`angle sinus.




Ainsi, la longueur de l`hypoténuse et du premier côté manquant du trapèze est d`environ 10,4566 cm.

8. Trouver la longueur de l`hypoténuse du deuxième triangle rectangle. Définissez la formule du sinus ( ) pour le deuxième angle intérieur donné. Cela vous donnera la longueur de l`hypoténuse, qui est aussi le premier côté du trapèze.
) pour le deuxième angle intérieur donné. Cela vous donnera la longueur de l`hypoténuse, qui est aussi le premier côté du trapèze.
 ) pour le deuxième angle intérieur donné. Cela vous donnera la longueur de l`hypoténuse, qui est aussi le premier côté du trapèze.
) pour le deuxième angle intérieur donné. Cela vous donnera la longueur de l`hypoténuse, qui est aussi le premier côté du trapèze.




Donc la longueur de l`hypoténuse et du deuxième côté manquant du trapèze est d`environ 8,4854 cm.

9. Mettre en place le théorème de Pythagore pour le premier triangle rectangle. Le théorème de Pythagore est fort  , où la longueur de l`hypoténuse est égale à
, où la longueur de l`hypoténuse est égale à  , et la hauteur du triangle
, et la hauteur du triangle  .
.
 , où la longueur de l`hypoténuse est égale à
, où la longueur de l`hypoténuse est égale à  , et la hauteur du triangle
, et la hauteur du triangle  .
.
dix. Utilisez les valeurs connues dans le théorème de Pythagore pour le premier triangle rectangle. Assurez-vous d`entrer la valeur correcte pour l`hypoténuse  et la hauteur
et la hauteur  .
.
 et la hauteur
et la hauteur  .
.

11. Résoudre ça pour b  . Cela vous donnera la longueur de la base du premier triangle rectangle, et la première partie manquante de la base du trapèze.
. Cela vous donnera la longueur de la base du premier triangle rectangle, et la première partie manquante de la base du trapèze.
 . Cela vous donnera la longueur de la base du premier triangle rectangle, et la première partie manquante de la base du trapèze.
. Cela vous donnera la longueur de la base du premier triangle rectangle, et la première partie manquante de la base du trapèze.





Donc la base du triangle et la première partie manquante du bas du trapèze mesure environ 8,5639 cm.

12. Trouver la longueur de la base manquante du deuxième triangle rectangle. Utilisez le théorème de Pythagore ( ). Utilisez la longueur de l`hypoténuse pour
). Utilisez la longueur de l`hypoténuse pour  et la hauteur pour
et la hauteur pour  . Résoudre ça pour
. Résoudre ça pour  et vous obtenez la longueur de la deuxième partie manquante du bas le trapèze.
et vous obtenez la longueur de la deuxième partie manquante du bas le trapèze.
 ). Utilisez la longueur de l`hypoténuse pour
). Utilisez la longueur de l`hypoténuse pour  et la hauteur pour
et la hauteur pour  . Résoudre ça pour
. Résoudre ça pour  et vous obtenez la longueur de la deuxième partie manquante du bas le trapèze.
et vous obtenez la longueur de la deuxième partie manquante du bas le trapèze.





Donc la base du deuxième triangle, et la deuxième partie manquante du bas du trapèze, est égale à 6 cm.

13. Ajouter tous les côtés du trapèze ensemble. Le périmètre d`un polygone est la somme de tous ses côtés :  . Pour le bas, ajoutez le bas du rectangle à la base des deux triangles.
. Pour le bas, ajoutez le bas du rectangle à la base des deux triangles.
 . Pour le bas, ajoutez le bas du rectangle à la base des deux triangles.
. Pour le bas, ajoutez le bas du rectangle à la base des deux triangles.
La circonférence approximative du trapèze est donc de 45,5059 cm.
Des astuces
- Utilisez les lois des triangles spéciaux pour trouver les longueurs manquantes des triangles spéciaux, sans utiliser la formule des sinus ou le théorème de Pythagore. Les lois s`appliquent à un triangle 30-60-90, ou un triangle 90-45-45.
- Utilisez une calculatrice scientifique pour déterminer le sinus d`un angle, en entrant l`angle, puis en appuyant sur le bouton « SIN ». Vous pouvez également utiliser une table de trigonométrie.
Nécessités
- Calculatrice
- Crayon
- Papier
Articles sur le sujet "Calculer le périmètre d'un trapèze"
Оцените, пожалуйста статью
Populaire