Enregistrez cette mesure comme une. Exemple: a = 2 cm 
A noter que cette étape calcule l`aire d`une face du cube. Exemple: a = 2 cm a = 2 x 2 = 4 cm 
Cette étape termine le calcul de l`aire du cube. Exemple: a = 4 cm Superficie = 6 x a = 6 x 4 = 24 cm 

Mesurez la longueur de la base pour déterminer la longueur du prisme et attribuez-la à c. Exemple: c = 5 cm Mesurez la largeur de la base pour déterminer la largeur du prisme et appelez-la une. Exemple: a = 2 cm Mesurez la hauteur du côté pour déterminer la hauteur du prisme et appelez-le b. Exemple: b = 3 cm 
Exemple: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 cm 
Exemple: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 cm 
Exemple: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 cm 
Exemple: Aire = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 cm. 

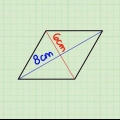
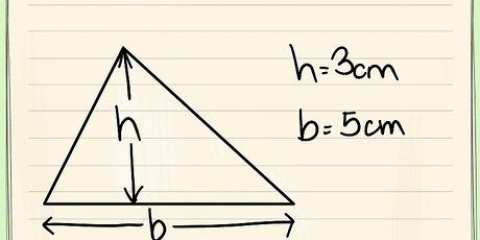
La base b, est égal à la longueur du bas du triangle. Exemple: b = 4 cm La hauteur h de la base triangulaire est égale à la distance entre le bord inférieur et la pointe. Exemple: h = 3 cm L`aire d`un triangle multipliée par 2 = 2(1/2)b*h = b*h = 4*3 =12 cm 
Exemple: H = 5cm Les trois côtés se réfèrent aux trois côtés de la base triangulaire. Exemple: S1 = 2 cm, S2 = 4 cm, S3 = 6 cm 
Exemple: P = S1 + S2 + S3 = 2 + 4 + 6 = 12 cm 
Exemple: P x H = 12 x 5 = 60 cm 
Exemple: 2A + PH = 12 + 60 = 72 cm. 

Exemple: r = 3 cm 
Exemple: r = r x r = 3 x 3 = 9 cm 
Exemple: *r = 3,14 x 9 = 28,26 cm 
Exemple: 4π*r = 4 x 28,26 = 113,04 cm 

Exemple: r = 3 cm Exemple: h = 5 cm 
Exemple : Aire de la base = π*r = 3,14 x 3 x 3 = 28,26 cm Exemple: 2π*r = 2 x 28,26 = 56,52 cm 
Exemple: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 cm 
Exemple: 2π*r + 2π*rh = 56,52 + 94,2 = 150,72 cm 

Exemple: l = 3 cm Exemple: s = 1 cm 
Exemple: s = s x s = 1 x 1 = 1 cm 
Exemple: 2 x s x l = 2 x 1 x 3 = 6 cm 
Exemple: s + 2sl = 1 + 6 = 7 cm 

Exemple: r = 2 cm Exemple: h = 4 cm 
Exemple: l = (r + h) = (2 x 2 + 4 x 4) = √ (4 + 16) = (20) = 4,47 cm 
Exemple: *r = 3,14 x 2 x 2 = 12,56 cm 
Exemple: *rl = 3,14 x 2 x 4,47 = 28,07 cm 
Exemple: *r + π*rl = 12,56 + 28,07 = 40,63 cm
Calculer la superficie
Teneur
L`aire est l`espace total occupé par toutes les aires d`un objet. C`est la somme de toutes les aires de cet objet. Déterminer l`aire d`une forme tridimensionnelle est assez facile, tant que vous utilisez la bonne formule. Chaque forme a sa propre formule distincte, vous devrez donc d`abord vérifier de quelle forme il s`agit. Le calcul de la formule de surface pour divers objets peut faciliter les calculs à l`avenir. Nous discutons ici de certaines des formes les plus courantes que vous pouvez rencontrer.
Pas
Méthode 1 sur 7: Cube

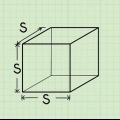
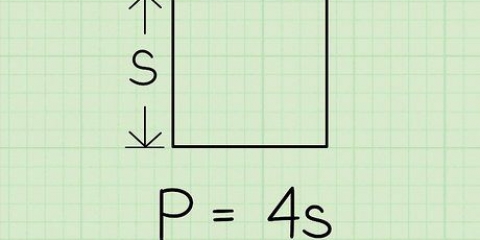
1. Définir la formule de l`aire d`un cube. Un cube a six faces identiques. Puisque la longueur et la largeur d`un carré sont égales, l`aire d`un carré est une, par lequel une la longueur est d`un côté. Puisqu`un cube a six faces égales, vous pouvez calculer son aire en multipliant l`aire de l`une de ses faces par six. La formule de l`aire d`un cube O est O = 6a, par lequel une la longueur est d`un côté.
- L`unité de surface est une certaine longueur au carré : cm, dm, m, etc.

2. Mesurer la longueur d`un côté. Par définition, chaque côté ou arête (arête) d`un cube doit être égal à l`autre, vous n`avez donc besoin de mesurer qu`un seul côté. Mesurer la longueur du côté avec une règle. Faites attention aux unités que vous utilisez.

3. Égalisez votre mesure pour une. Carré de la mesure pour calculer la longueur de la côte. Carré une valeur signifie la multiplier par elle-même. Si vous apprenez cela pour la première fois, il peut être utile de vous en souvenir car NT= 6*a*a.

4. Multipliez ce produit par six. Rappelez-vous qu`un cube a six faces identiques. Maintenant que vous connaissez l`aire d`une des faces, multipliez-la par six (à cause des six faces).
Méthode 2 sur 7 : Prisme rectangulaire

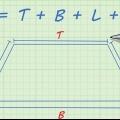
1. Définir la formule de l`aire d`un prisme rectangulaire. Comme un cube, un prisme rectangulaire a six faces, mais contrairement à un cube, ces faces ne sont pas égales. Dans un prisme rectangulaire, seules les faces opposées sont égales les unes aux autres. Par conséquent, lors du calcul de l`aire d`un prisme rectangulaire, les différentes longueurs des nervures doivent être prises en compte, comme dans la formule SA = 2ab + 2bc + 2ac.
- Pour cette formule, une égale à la largeur du prisme, b égal à la hauteur et c égal à la longueur.
- Si nous regardons de plus près la formule, vous verrez que nous additionnons simplement toutes les zones de chaque face de l`objet.
- L`unité de surface sera une certaine longueur au carré : cm, dm, m, etc.

2. Mesurer la longueur, la hauteur et la largeur de chaque côté. Les trois lectures peuvent être différentes, chacune doit donc être mesurée séparément. Mesurez chaque côté avec une règle et notez la valeur. Utilisez les mêmes unités pour chaque mesure.

3. Calculer l`aire d`une des faces du prisme, et la multiplier par deux. Rappelez-vous qu`il y a six faces dans un prisme rectangulaire et que les faces opposées sont égales les unes aux autres. Multipliez la longueur et la hauteur, ou c et une, pour trouver l`aire d`un avion. Prenez cette mesure et multipliez-la par deux pour tenir compte du plan identique opposé.

4. Trouvez l`aire de l`autre face du prisme et multipliez-la par deux. Comme pour le premier ensemble de faces, multipliez la largeur et la hauteur, ou une et b pour déterminer l`aire d`une autre face du prisme. Multipliez cette mesure par deux pour tenir compte des côtés identiques opposés.

5. Calculez l`aire des extrémités du prisme et multipliez-la par deux. Les deux autres faces du prisme sont les extrémités. Multipliez la longueur et la largeur (c et b) pour trouver leur surface. Multipliez cette zone par deux pour tenir compte des deux côtés.

6. Ajouter les trois zones distinctes ensemble. Étant donné que l`aire du prisme est l`aire totale de toutes les faces d`un objet, la dernière étape consiste à additionner toutes les aires calculées individuellement. Additionnez les surfaces de tous les côtés pour obtenir la surface totale.
Méthode 3 sur 7 : Prisme triangulaire

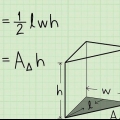
1. Définir la formule d`aire d`un prisme triangulaire. Un prisme triangulaire a deux faces triangulaires identiques et trois faces rectangulaires. Pour trouver l`aire, il faut calculer l`aire de tous les visages et les additionner. L`aire d`un prisme triangulaire est SA = 2A + PH, où A est l`aire de la base triangulaire, P est le périmètre de la base triangulaire et h est la hauteur du prisme.
- Car cette formule tient que une la aire d`un triangle Et ainsi A = 1/2bh, par lequel b est la base du triangle et h la hauteur.
- p est le périmètre du triangle calculé en additionnant les trois arêtes du triangle.
- L`unité de surface est une unité de longueur au carré : cm, dm, m, etc.

2. Calculez l`aire du plan triangulaire et multipliez-la par deux. L`aire d`un triangle est /2b*h où b est la base du triangle et h est la hauteur. Donc puisqu`il y a deux triangles identiques comme faces, on multiplie la formule par deux. Cela rend le calcul pour les deux plans facile (b*h).

3. Mesurez chaque côté du triangle et la hauteur du prisme. Pour terminer le calcul de l`aire, vous devez connaître la longueur de chaque côté du triangle et la hauteur du prisme. La hauteur est la distance entre les deux faces triangulaires.

4. Trouver le périmètre du triangle. Le périmètre du triangle peut être calculé en additionnant tous les côtés mesurés : S1 + S2 + S3.

5. Multiplier la circonférence de la base par la hauteur du prisme. Rappelez-vous que la hauteur du prisme est la distance entre les deux faces triangulaires. En d`autres termes, multipliez p de hein.

6. Additionner les deux lectures distinctes ensemble. Vous devez additionner les deux mesures des deux étapes précédentes pour obtenir l`aire du prisme triangulaire.
Méthode 4 sur 7 : Bol

1. Définir la formule d`aire d`une sphère. Une sphère a une surface courbe, donc la surface est une valeur multipliée par la constante, pi. L`aire d`une sphère est calculée à l`aide de l`équation NT = 4π*r.
- Pour cette formule, r égal au rayon de la sphère. Pi (ou π) peut être arrondi à 3,14.
- Les unités de la zone seront une unité de longueur, au carré : cm, dm, m, etc.

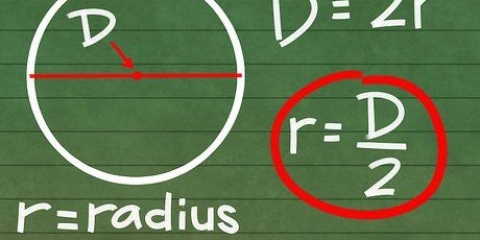
2.Mesurer le rayon de l`ampoule. Le rayon de la sphère est la moitié du diamètre, ou la distance du centre de la sphère au bord.

3. Carré du rayon. Pour mettre un nombre au carré, multipliez-le par lui-même. Multipliez la mesure pour r avec lui-même. Rappelez-vous que cette formule peut être réécrite comme SA = 4π*r*r.

4. Multiplier le rayon au carré par un arrondi de pi. Pi est une constante qui représente le rapport de la circonférence d`un cercle à son diamètre. C`est un nombre irrationnel avec de nombreux chiffres après la virgule. Il est souvent arrondi à 3,14. Multipliez le rayon carré par , ou 3,14, pour l`aire d`une section transversale circulaire de la sphère.

5. Multipliez ce produit par quatre. Pour terminer le calcul, multipliez-le par quatre. Trouvez l`aire de la sphère en multipliant l`aire circulaire plate par quatre.
Méthode 5 sur 7: Cylindre

1. Définir la formule d`aire d`un cylindre. Un cylindre a deux extrémités circulaires fermant une surface tubulaire. La formule de l`aire d`un cylindre est NT = 2π*r + 2π*rh, par lequel r est égal au rayon de la base circulaire et h égale la hauteur du cylindre. Autour de pi (ou π) diminue à 3,14.
- La formule 2π*r calcule l`aire des deux extrémités circulaires, tandis que 2πrh est l`aire de la colonne entre les deux extrémités.
- Les unités de surface sont une unité de longueur au carré : cm, dm, m, etc.

2. Mesurer le rayon et la hauteur du cylindre. Le rayon d`un cercle est la moitié de son diamètre, ou la distance du centre du cercle au bord. La hauteur est la distance totale du cylindre d`une extrémité à l`autre. Dessinez ces mesures avec une règle et notez-les.

3. Trouvez l`aire de la base et multipliez-la par deux. Pour trouver l`aire de la base, utilisez la formule de l`aire ou un cercle (π*r). Pour terminer le calcul, mettez le rayon au carré et multipliez-le par pi. Multipliez ensuite par deux à cause du deuxième cercle identique à l`autre extrémité du cylindre.

4. Calculer la surface du cylindre lui-même avec 2π*rh. C`est la formule pour calculer l`aire d`un tube. Le tube est l`espace entre les deux extrémités circulaires du cylindre. Multiplier le rayon par deux, pi et la hauteur.

5. Additionner les deux lectures distinctes ensemble. Ajouter l`aire des deux cercles à l`aire de l`espace entre les deux cercles pour calculer l`aire totale du cylindre. Remarque : En ajoutant ces deux pièces, vous reconnaissez la formule originale : NT =2π*r + 2π*rh.
Méthode 6 sur 7 : Pyramide carrée

1. Définir la formule d`aire d`une pyramide carrée. Une pyramide carrée a une base carrée et quatre côtés triangulaires. Comme mentionné, l`aire d`un carré est la longueur d`un côté au carré. L`aire d`un triangle est 1/2sl (le côté du triangle multiplié par la longueur ou la hauteur du triangle). Puisqu`il y a quatre triangles, vous calculez l`aire totale en multipliant cela par quatre. L`addition de toutes ces faces donne l`équation de l`aire d`une pyramide carrée : NT = s + 2 canaux.
- Dans cette équation, s la longueur de chaque côté de la base carrée et je la hauteur d`inclinaison de chaque côté triangulaire.
- L`unité de surface est une certaine unité de longueur au carré : cm, dm, m, etc.

2. Mesurer la hauteur inclinée et le côté de la base. La hauteur oblique je, est la hauteur de l`un des côtés triangulaires. C`est la distance de la base à la pointe de la pyramide, mesurée le long d`un côté plat. Le côté basique s, est la longueur d`un côté de la base carrée. Puisque la base est carrée, cette mesure est la même pour tous les côtés. Utilisez une règle pour chaque mesure.

3. Trouver l`aire de la base carrée. L`aire d`une base carrée peut être calculée en multipliant au carré la longueur d`un côté (s multiplier par lui-même).

4. Calculer l`aire totale des quatre faces triangulaires. La deuxième partie de l`équation est l`aire des quatre faces triangulaires restantes. En utilisant la formule 2ls, on multiplie s de je et deux. Trouver la zone de chaque visage.

5. Ajouter les deux zones distinctes ensemble. Ajouter la surface totale des faces à la surface de la base pour calculer la surface totale.
Méthode 7 sur 7: Cône

1. Définir la formule d`aire d`un cône. Un cône a une base circulaire et une surface ronde qui se rétrécit en un point. Pour trouver l`aire, prenez l`aire de la base circulaire et l`aire du cône, et additionnez les deux. La formule de l`aire d`un cône est : SA = *r + π*rl, par lequel r le rayon est de la base circulaire, je la hauteur oblique du cône, et est la constante pi (3.14).
- L`unité de surface est une certaine unité de longueur au carré : cm, dm, m, etc.

2. Mesurer le rayon et la hauteur du cône. Le rayon est la distance entre le centre de la base circulaire et le bord de la base. La hauteur est la distance entre le centre de la base et la pointe du cône, mesurée par le centre du cône.

3. Calculer la hauteur de la pente (je) du cône. Puisque la hauteur oblique est l`hypoténuse réelle d`un triangle, vous devez trouver la en utilisant le théorème de Pythagore pour le calculer. Utiliser la forme réorganisée, l = (r + h), par lequel r le rayon est et h la hauteur du cône.

4. Trouver l`aire de la base circulaire. L`aire de la base est calculée avec la formule π*r. Après avoir mesuré le rayon, vous le carré (donc vous le multipliez par lui-même) puis vous multipliez ce produit par pi.

5. Calculer l`aire du sommet du cône. Utilisez la formule *rl, où r le rayon est du cercle et je la pente telle que calculée ci-dessus, pour déterminer l`aire du sommet du cône.

6. Additionnez les deux zones ensemble pour obtenir la surface totale du cône. Calculez l`aire finale du cône en ajoutant l`aire de la base circulaire lors du calcul de l`étape précédente.
Nécessités
- Règle
- Stylo ou crayon
- Papier
Articles sur le sujet "Calculer la superficie"
Оцените, пожалуйста статью
Populaire