Calculer l'apothème d'un hexagone : 15 étapes (avec photos)

Teneur

Pas
- Méthode 1 sur 2: Utilisation du théorème de Pythagore (la longueur du rayon est donnée)
- Méthode 2 sur 2: Utilisation de la trigonométrie (et d`un rayon donné)
Des astuces

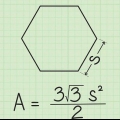
Un hexagone est un polygone avec six angles et côtés. Lorsqu`un hexagone est régulier, il a six côtés égaux et un apothème. Un apothème est un segment de ligne allant du centre d`un polygone au centre de chaque côté. Habituellement, la longueur de l`apothème doit être donnée pour calculer l`aire d`un hexagone. Tant que vous connaissez la longueur du côté de l`hexagone, vous pouvez calculer la longueur de l`apothème.

Pas

Méthode 1 sur 2: Utilisation du théorème de Pythagore (la longueur du rayon est donnée)

Image intitulée Calculer l`apothème d`un hexagone Étape 1

1. Divisez l`hexagone en six triangles équilatéraux congrus. Pour ce faire, tracez une ligne à partir de chaque sommet ou point, jusqu`au sommet opposé.

Image intitulée Calculer l`apothème d`un hexagone Étape 2

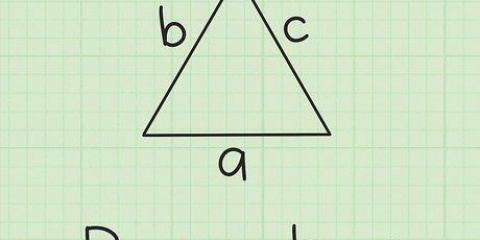
2. Choisissez un triangle et notez la longueur de la base. Il est égal à la longueur du côté de l`hexagone.

Par exemple, vous avez un hexagone d`une longueur de 8 cm pour le côté. La base de tout triangle équilatéral est donc de 8 cm.

Image intitulée Calculer l`apothème d`un hexagone Étape 3

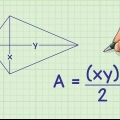
3. Faire deux triangles rectangles. Pour ce faire, tracez une ligne à partir du sommet supérieur du triangle équilatéral perpendiculaire à la base. Cette ligne coupera la base du triangle (c`est donc l`apothème de l`hexagone). Étiquetez la longueur de la base de l`un des triangles rectangles.

Par exemple, si la base du triangle équilatéral est de 8 cm, alors la base de tout triangle rectangle - lorsque vous divisez le triangle en deux triangles rectangles - est maintenant égale à 4 cm.

Image intitulée Calculer l`apothème d`un hexagone Étape 4

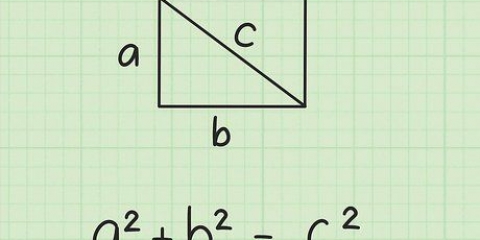
4. Utiliser le théorème de Pythagore. La formule est

une 2 + b^{2} = c^{2}

$a^{{2}}+b^{{2}}=c^{{2}}$ , par lequel

c

$c$ est égal à la longueur de l`hypoténuse (le côté opposé à l`angle droit), et

une

$une$ et

b

$b$ être égal aux longueurs des deux autres côtés du triangle.

Par exemple, si le triangle rectangle a une hypoténuse de

2

$2$ un côté de

1

$1$ et un autre côté d`environ

1, 732

$1732$ (

\sqrt{3}

${sqrt{3}}$ ), alors le théorème de Pythagore dit que

12 + {\sqrt{3}}^{2} = 2^{2}

$1^{{2}}+{sqrt{3}}^{{2}}=2^{{2}}$ , ce qui est correct lorsque vous calculez ceci :

1 + 3 = 4

$1+3=4$ .

Image intitulée Calculer l`apothème d`un hexagone Étape 5

5. Remplacer la longueur de la base du triangle rectangle dans la formule. Substitut

b

$b$ .

Par exemple, si la longueur de la base est de 4, votre formule ressemblera à ceci :

une 2 + 4^{2} = c^{2}

$a^{{2}}+4^{{2}}=c^{{2}}$ .

Image intitulée Calculer l`apothème d`un hexagone Étape 6

6. Remplacer la longueur de l`hypoténuse dans la formule. Vous connaissez la longueur de l`hypoténuse car vous connaissez la longueur de l`hexagone. La longueur du côté d`un hexagone régulier est égale au rayon de l`hexagone. Le rayon est une ligne reliant le centre d`un polygone à l`un de ses sommets. Vous verrez que l`hypoténuse du triangle rectangle est aussi le rayon de l`hexagone, donc la longueur du côté de l`hexagone est égale à la longueur de l`hypoténuse.

Par exemple, si la longueur du côté de l`hexagone est de 8 cm, alors la longueur de l`hypoténuse du triangle rectangle est également de 8 cm. Donc votre formule ressemblera maintenant à ceci :

une 2 + 4^{2} = 8^{2}

$a^{{2}}+4^{{2}}=8^{{2}}$ .

Image intitulée Calculer l`apothème d`un hexagone Étape 7

sept. Au carré les valeurs connues de la formule. Rappelez-vous que la quadrature d`un nombre revient à multiplier ce nombre par lui-même.

Par exemple, après avoir mis au carré les valeurs connues, votre formule ressemblera à ceci :

une 2 + 16 = 64

$a^{{2}}+16=64$ .

Image intitulée Calculer l`apothème d`un hexagone Étape 8

8. Isoler la variable inconnue. Vous faites cela en soustrayant la valeur au carré

b

$b$ des deux côtés de l`équation.

Par exemple:

une 2 + 16 - 16 = 64 - 16

$a^{{2}}+16-16=64-16$

une 2 = 48

$a^{{2}}=48$

Image intitulée Calculer l`apothème d`un hexagone Étape 9

9. Résoudre pour une{style d`affichage a} $une$ . Pour ce faire, déterminez la racine carrée de chaque côté de l`équation. Cela vous donnera la longueur du côté manquant du triangle, qui est égale à la longueur de l`apothème de l`hexagone.

Par exemple, à l`aide d`une calculatrice, vous calculez

\sqrt{48} = 6, 93

${sqrt{48}}=6.93$ . Donc la longueur manquante du triangle rectangle, et donc la longueur de l`apothème de l`hexagone, est égale à 6,93 cm.

Méthode 2 sur 2: Utilisation de la trigonométrie (et d`un rayon donné)

Image intitulée Calculer l`apothème d`un hexagone Étape 10

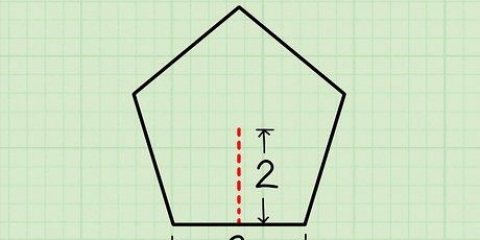
1. Écrivez la formule pour trouver l`apothème d`un polygone régulier. La formule est

apothème = s 2 bronzer ?? (\frac{180}{m})

${text{apothema}}={frac{s}{2tan({frac{180}{n}})}}$ , par lequel

s

$s$ est égal à la longueur du côté du polygone et

m

$m$ est égal au nombre de côtés du polygone.

Image intitulée Calculer l`apothème d`un hexagone Étape 11

2. Remplacer la longueur du côté dans la formule. N`oubliez pas de remplacer la variable

s

$s$ .

Par exemple, pour un hexagone de 8 cm de côté, la formule ressemblerait à ceci :

8 2 bronzer ?? (\frac{180}{m})

${frac{8}{2tan({frac{180}{n}})}}$ .

Image intitulée Calculer l`apothème d`un hexagone Étape 12

3. Entrez le nombre de côtés dans la formule. Un hexagone a 6 côtés. N`oubliez pas de remplacer la variable

m

$m$ .

Par exemple:

8 2 bronzer ?? (\frac{180}{6})

${frac{8}{2tan({frac{180}{6}})}}$ .

Image intitulée Calculer l`apothème d`un hexagone Étape 13

4. Arrondissez le calcul entre parenthèses. Cela vous donne le nombre de degrés nécessaires pour calculer la tangente.

Par exemple,

\frac{180}{6} = 30

${frac{180}{6}}=30$ , avec laquelle la formule ressemble maintenant à ceci :

8 2 bronzer ?? (30)

${frac{8}{2tan(30)}}$ .

Image intitulée Calculer l`apothème d`un hexagone Étape 14

5. Déterminer la tangente. Utilisez une calculatrice ou une table trigonométrique pour cela.

Par exemple, la tangente de 30 est d`environ 0,577, donc la formule ressemblerait à ceci :

8 2 (0, 577)

${frac{8}{2(0,577)}}$ .

Image intitulée Calculer l`apothème d`un hexagone Étape 15

6. Multipliez la tangente par 2 puis divisez la longueur d`un côté par ce nombre. Avec cela, vous avez calculé la longueur de l`apothème de votre hexagone.

Par exemple:

apothème = 8 2 (0, 577)

${text{apothema}}={frac{8}{2(0,577)}}$

apothème = 8 1, 154

${text{apothema}}={frac{8}{1154}}$

apothème = 6, 93

${text{apothema}}=6.93$
Donc l`apothème d`un hexagone régulier avec des côtés de 8 cm est d`environ 6,93 cm.

Des astuces

Le terme « apothema » peut faire référence au segment de ligne réel ou à la longueur de ce segment de ligne.
N`oubliez pas que cette méthode ne fonctionne que pour les hexagones réguliers. Les hexagones irréguliers n`ont pas d`apothème.