Ex. 2 x 32 = 64. 
Ex. 64 = 8. 






Ex. 2.878521796 / 3 = 0.959507265… 
Ex. log inverse 0,959507265 = 9,109766916. Donc la moyenne géométrique de 7, 9 et 12 est égale à 9.11. La moyenne géométrique de tout ensemble de nombres est toujours inférieure ou égale à la moyenne arithmétique de cet ensemble. La moyenne géométrique ne s`applique qu`aux nombres positifs. Dans les problèmes où le calcul de la moyenne géométrique est demandé, cela n`a généralement pas de sens de travailler avec des nombres négatifs.
Calcul de la moyenne géométrique
Teneur
La moyenne géométrique est un terme mathématique lié à, et souvent confondu avec, la moyenne arithmétique plus couramment utilisée. Pour calculer la moyenne géométrique, nous utilisons l`une des méthodes ci-dessous.
Pas
Méthode 1 sur 4 : Deux nombres : méthode facile

1. Déterminez les nombres dont vous voulez calculer la moyenne de.
- Ex. 2 et 32.

2. Multipliez-les ensemble.

3. Calculer la racine carrée du produit obtenu.
Méthode 2 sur 4 : Deux nombres : méthode détaillée

1. Commencez à remplir les nombres dans l`équation ci-dessous. Par exemple, si vous travaillez avec les nombres 10 et 15, entrez 10 et 15 comme indiqué ci-dessous.

2. Résoudre pour x. Démarrer la multiplication croisée. Puisque x*x = x, votre équation ressemblera à ceci : x = (produit des deux autres nombres). Pour résoudre x, trouvez la racine carrée de ce produit. Avec un peu de chance, cela sortira avec un entier. Si ce n`est pas le cas, donnez le nombre en décimales, ou laissez la racine carrée, selon les besoins. L`exemple donné est sous la forme d`une racine carrée.
Méthode 3 sur 4 : Trois nombres ou plus : Méthode simple

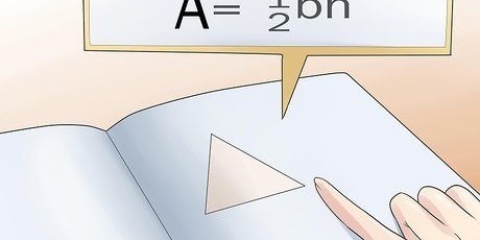
1. Remplacez vos nombres dans l`équation ci-dessous. Moyenne = (un1 × un2 ×. . .× unm)
- une1 est votre premier numéro et un2 est le deuxième nombre, et ainsi de suite
- n est le nombre de nombres

2. Multipliez les nombres a1, une2, etc. avec l`un l`autre.

3. Calculez le mracine de ce nombre. C`est la moyenne géométrique.
Méthode 4 sur 4: Trois nombres ou plus : Logarithmes

1. Trouvez le journal de chaque nombre et additionnez ces valeurs. Trouvez le bouton LOG sur votre calculatrice. Tapez maintenant : (premier nombre) LOG + (deuxième nombre) LOG + (troisième nombre) LOG [+ journal des nombres suivants, le cas échéant] =. N`oubliez pas de vérifier le = sinon vous ne verrez que le journal du dernier numéro, pas le total.
- Ex. log 7 + log 9 + log 12 = 2.878521796…

2. Divisez la somme des valeurs logarithmiques par le nombre de nombres que vous avez additionnés. Lorsque vous avez additionné les journaux des trois nombres, divisez par trois.

3. Trouver l`inverse du log du résultat. Comment cela fonctionne sur une calculatrice dépend du fabricant, mais chaque bon a une fonction inverse. Consultez votre manuel pour savoir où il se trouve. Le log inverse dans ce cas est la moyenne géométrique.
Des astuces
- La différence entre la moyenne arithmétique et géométrique :
- Si vous moyenne arithmétique si vous voulez calculer 3, 4 et 18 alors faites 3 + 4 + 18 et divisez cette somme par 3 (car il y a trois nombres). Donc 25/3 = 8,333.... La moyenne arithmétique répond à la question, "Si tous les nombres sont égaux, que devraient être ces nombres pour obtenir le même total ??"
- Ce Moyenne géométrique répond correctement à la question, "Si tous les nombres sont de la même taille, que devraient être ces nombres à multiplier pour obtenir le même total ??" Donc pour trouver la moyenne géométrique de 3, 4 et 18, on ferait 3 x 4 x 18 = 216. Ensuite, nous prenons la racine cubique de ceci (car il y a trois nombres). La réponse est 6. En d`autres termes, puisque 6 x 6 x 6 = 3 x 4 x 18, 6 est la moyenne géométrique de 3, 4 et 18.
Articles sur le sujet "Calcul de la moyenne géométrique"
Оцените, пожалуйста статью
Populaire