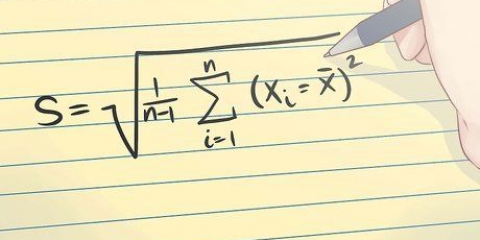Dans l`exemple de collecte de données, ces écarts deviennent : 







Pour vérifier la validité de vos calculs, nous vérifions si la somme des valeurs dans la colonne des écarts est égale à zéro. Si vous additionnez tous les écarts et que vous obtenez autre chose que zéro, alors votre moyenne est incorrecte ou vous avez fait une erreur dans le calcul d`un ou plusieurs des écarts. Retournez et vérifiez votre travail. 
La valeur absolue est un outil mathématique pour indiquer la distance ou la magnitude, quelle que soit la direction. Pour déterminer la valeur absolue, omettez simplement le signe moins pour chaque nombre dans la deuxième colonne. Remplissez donc la troisième colonne avec les valeurs absolues comme suit : 









Pour cet ensemble de données, le calcul final sera : 

Par exemple, avec cet ensemble de données, vous pouvez dire que la moyenne est de neuf et la distance moyenne de la moyenne est de 2,75. Notez que certaines valeurs sont plus proches de 2,75 par rapport à d`autres. Mais 2,75 est la distance moyenne.
Calcul de l'écart moyen par rapport à la moyenne
Teneur
Lorsque vous travaillez avec des données, il existe plusieurs façons de mesurer à quel point vos valeurs de données sont regroupées. Le plus commun est la moyenne. La plupart des gens apprennent à calculer la moyenne tôt à l`école en trouvant la somme d`un groupe de valeurs de données, puis en divisant par le nombre de valeurs dans le groupe. Un calcul plus avancé est l`écart moyen sur la moyenne. Ce calcul vous indique à quel point vos valeurs sont proches de la moyenne. Vous déterminez cela en trouvant la moyenne d`un ensemble de données, puis l`écart de chaque donnée par rapport à cette moyenne, puis la moyenne de ces écarts.
Pas
Partie 1 sur 2: Calcul de la moyenne

1. Collectez et comptez vos données. Pour tout ensemble de valeurs, la moyenne est une mesure de la valeur centrale. Selon le type de données, la moyenne vous donnera la valeur médiane de ces données. Pour trouver la moyenne, vous devez d`abord collecter vos données, soit par le biais d`une expérience, soit simplement lors d`une mission.
- Comme exemple, nous utilisons une séquence de nombres donnée 6, 7, 10, 12, 13, 4, 8 et 12. Cette séquence est suffisamment petite pour compter à la main, et voir rapidement qu`il s`agit d`une séquence de huit nombres.
- Dans la statistique, la variable
ou
souvent utilisé pour indiquer le nombre de valeurs dans une série ou une collection.

2. Trouver la somme des valeurs. La première étape pour déterminer la moyenne consiste à calculer la somme de toutes les valeurs. Dans la notation statistique, chaque valeur est généralement représentée par la variable  . La somme de toutes les valeurs reçoit le symbole
. La somme de toutes les valeurs reçoit le symbole  . La lettre majuscule grecque sigma indique que c`est la somme des valeurs. Le calcul pour cette série simple va comme ceci :
. La lettre majuscule grecque sigma indique que c`est la somme des valeurs. Le calcul pour cette série simple va comme ceci :
 . La somme de toutes les valeurs reçoit le symbole
. La somme de toutes les valeurs reçoit le symbole  . La lettre majuscule grecque sigma indique que c`est la somme des valeurs. Le calcul pour cette série simple va comme ceci :
. La lettre majuscule grecque sigma indique que c`est la somme des valeurs. Le calcul pour cette série simple va comme ceci :

3. Partagez pour trouver la moyenne. Enfin, divisez la somme par le nombre de valeurs. La lettre grecque mu,  , est souvent utilisé pour indiquer la moyenne. Le calcul de la moyenne se déroule donc comme suit :
, est souvent utilisé pour indiquer la moyenne. Le calcul de la moyenne se déroule donc comme suit :
 , est souvent utilisé pour indiquer la moyenne. Le calcul de la moyenne se déroule donc comme suit :
, est souvent utilisé pour indiquer la moyenne. Le calcul de la moyenne se déroule donc comme suit :
Partie 2 sur 2: Détermination de l`écart moyen

1. Créer un tableau. Pour garder vos données en ordre et pour vous aider dans les calculs, il est utile de créer un tableau de trois colonnes. Étiqueter la première colonne  . Étiqueter la deuxième colonne
. Étiqueter la deuxième colonne  . Étiqueter la troisième colonne
. Étiqueter la troisième colonne  .
.
 . Étiqueter la deuxième colonne
. Étiqueter la deuxième colonne  . Étiqueter la troisième colonne
. Étiqueter la troisième colonne  .
. - Remplissez la première colonne avec les valeurs pour votre calcul.

2. Calculer l`écart (déviation) de chaque valeur. Dans la deuxième colonne, intitulée  , mettre l`écart ou la différence entre chaque valeur et la moyenne de la série ou de l`ensemble. Trouvez cette valeur en soustrayant la moyenne de chaque valeur de données.
, mettre l`écart ou la différence entre chaque valeur et la moyenne de la série ou de l`ensemble. Trouvez cette valeur en soustrayant la moyenne de chaque valeur de données.
 , mettre l`écart ou la différence entre chaque valeur et la moyenne de la série ou de l`ensemble. Trouvez cette valeur en soustrayant la moyenne de chaque valeur de données.
, mettre l`écart ou la différence entre chaque valeur et la moyenne de la série ou de l`ensemble. Trouvez cette valeur en soustrayant la moyenne de chaque valeur de données.








3. Déterminer la valeur absolue de chaque écart. Lorsque vous calculez l`écart de n`importe quelle valeur par rapport à la moyenne, vous voulez seulement connaître la différence, pas si cette différence est positive ou négative. Ce dont vous avez vraiment besoin, en termes mathématiques, c`est la valeur absolue de la différence. La valeur absolue est indiquée par des barres verticales| |.










4. Calculer la moyenne des écarts absolus. Après avoir rempli le tableau à trois colonnes, trouvez la moyenne des valeurs absolues dans la troisième colonne. Tout comme vous l`avez fait pour calculer la moyenne des valeurs initiales, additionnez les écarts et divisez la somme par le nombre de valeurs.


5. Interpréter le résultat. La valeur de l`écart moyen par rapport à la moyenne est une mesure de la proximité des valeurs les unes par rapport aux autres. Cela répond à la question « À quelle distance de la moyenne les valeurs des données sont-elles en moyenne ? »?`
Des astuces
- Continuez à pratiquer et vous pourrez le calculer en douceur.
Articles sur le sujet "Calcul de l'écart moyen par rapport à la moyenne"
Оцените, пожалуйста статью
Populaire