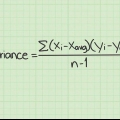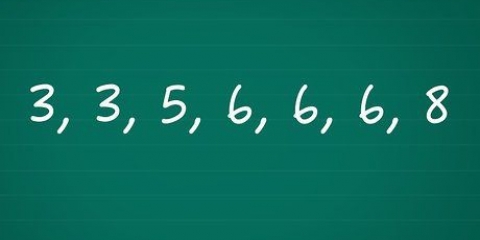Calcul de la variance : 8 étapes (avec photos)

Teneur

Pas
Des astuces

Le calcul de la variance vous permet de mesurer la dispersion d`un ensemble de valeurs - le degré auquel un certain nombre de valeurs diffèrent les unes des autres. La variance est l`une des composantes de la distribution de probabilité et indique dans quelle mesure les valeurs s`écartent de la moyenne. La variance est souvent utilisée avec l`écart type (la racine carrée de la variance). Si vous voulez savoir comment calculer la variance d`un ensemble de valeurs, suivez les étapes ci-dessous.

Pas

1. Ecrire la formule pour calculer la variance. L`estimation pour calculer une estimation aléatoire de la variance de la population à partir d`un échantillon fixe de n observations est la définition suivante :(s) = [(x_je - x̅)]/n - 1. La formule de calcul de la variance dans une population entière est la même que la précédente, sauf que le dénominateur n`est pas égal à n – 1, mais à n. Tant qu`il s`agit d`un ensemble fini d`observations, il vaut mieux utiliser la première formule. Voici une explication des variables de la formule :

s = Écart
Σ = Sommation, la somme de tous les termes de l`équation après le signe de sommation.
X_je = Les exemples de valeurs.
x̅ = La moyenne des valeurs de la série.
n = La taille de l`échantillon. Le nombre de valeurs dans la série.

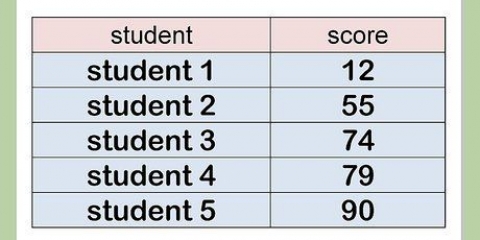
2. Calculer la somme des valeurs de la série. Créez d`abord un tableau avec une colonne pour les valeurs, la valeur moins la moyenne (x_je - x̅) puis le carré de ces termes [(x_je - X))]. Une fois que vous avez terminé avec le tableau et rempli la première colonne, additionnez toutes les valeurs de la série. Supposons que vous ayez affaire à la séquence de nombres suivante : 17, 15, 23, 7, 9, 13. Additionné ceci est : 17 + 15 + 23 + 7 + 9 + 13 = 84.

3. Calculer la moyenne. Divisez la somme des nombres de la série par le nombre d`éléments de la série pour calculer la moyenne. Donc dans ce cas la somme 84 divisée par le nombre de nombres, 6. 84/6 = 14. écrivez "14" tout en bas de la colonne en moyenne.

4. Soustraire la moyenne de chaque valeur de la série. Soustraire 14 de chaque valeur de la série et remplir la troisième colonne (la moyenne de l`échantillon). Vous pouvez vérifier votre travail en vérifiant si la somme de tous les résultats est nulle. Voici comment calculer l`écart par rapport à la moyenne pour chaque valeur de la série :

17 - 14 = 3

15 - 14 = 1

23 - 14 = 9

7 - 14 = -7

9 - 14 = -5

13 - 14 = -1

5. Carré chaque résultat. Après avoir calculé l`écart par rapport à la moyenne, placez-le au carré et écrivez la réponse dans la quatrième colonne. Donc toutes les réponses sont positives. Voici comment cela a fonctionné :

3 = 9

1 = 1

9 = 81

(-7)= 49

(-5) = 25

(-1)= 1

6. Calculer la somme des carrés. Additionner les résultats ensemble. 9 + 1 + 81 + 49 + 25 + 1 = 166

sept. Substituer les valeurs dans l`équation. Remplissez les valeurs dans l`équation. Souviens-toi que "m" représente le nombre d`éléments dans la séquence.

s = 166/(6-1)

8. Résoudre. Divisez maintenant 166 par 5. Le résultat est 33,2. Si vous voulez aussi connaître l`écart type, trouvez la racine carrée de 33,2. √33,2 = 5,76. Vous pouvez maintenant commencer à interpréter ces données par rapport à la situation dans son ensemble. Habituellement, la variance de deux séries est comparée. La valeur la plus basse signifie que dans cette série la variance est moins grande.