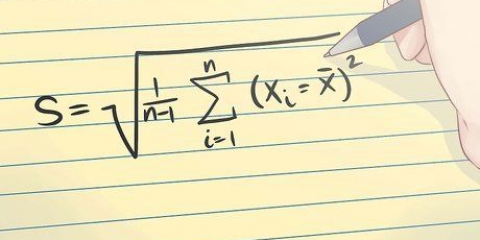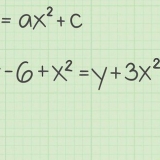Calculer la somme des carrés (sse)

Teneur

La somme des carrés, ou SSE, est un calcul statistique préliminaire qui conduit à différentes valeurs de données. Lorsque vous disposez d`un ensemble de valeurs de données, il est utile de pouvoir déterminer à quel point ces valeurs sont liées les unes aux autres. Vous devez organiser vos données dans un tableau et ensuite faire des calculs assez simples. Une fois que vous avez trouvé le SSE pour un ensemble de données, vous pouvez alors trouver la variance et l`écart type.

Pas

Méthode 1 sur 3: Calculer le SSE à la main

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 1

1. Faire un tableau de trois colonnes. La façon la plus simple de calculer le SSE est de commencer avec un tableau de trois colonnes. Étiquetez les trois colonnes

Où le

${displaystyle {text{Valeur}}}$ ,

déviation

${displaystyle {text{Déviation}}}$ , et

déviation 2

${displaystyle {text{Déviation}}^{2}}$ .

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 2

2. Remplissez les détails. La première colonne contient les valeurs de vos mesures. Remplir la colonne

Où le

${displaystyle {text{Valeur}}}$ avec tes lectures. Cela peut être le résultat d`une expérience, d`une étude statistique ou simplement des données d`un problème mathématique.

Dans ce cas, supposons que vous travaillez avec des données médicales et que vous ayez une liste des températures corporelles de dix patients. La température corporelle normale attendue est de 98,6 degrés. La température de dix patients est mesurée et donne les valeurs 99,0, 98,6, 98,5, 101,1, 98,3, 98,6, 97,9, 98,4, 99,2 et 99,1. La température de dix patients est mesurée et donne les valeurs 99,0, 98,6, 98,5, 101,1, 98,3, 98,6, 97,9, 98,4, 99,2 et 99,1. Écrivez ces valeurs dans la première colonne.

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 3

3. Calculer la moyenne. Avant de pouvoir calculer l`erreur pour chaque mesure, vous devez calculer la moyenne de l`ensemble des données.

La moyenne d`un ensemble de données est la somme de ses valeurs divisée par le nombre de valeurs dans l`ensemble. Ceci peut être représenté symboliquement, avec la variable

??

$mu$ :

?? = ?? X m

${displaystyle mu ={frac {Sigma x}{n}}}$

Pour ces données, la moyenne est calculée comme suit :

?? = 99, 0 + 98, 6 + 98, 5 + 101, 1 + 98, 3 + 98, 6 + 97, 9 + 98, 4 + 99, 2 + 99, 1 dix

${displaystyle mu ={frac {99,0+98,6+98,5+101,1+98,3+98,6+97,9+98,4+99,2+99,1} {10}}}$

?? = 988, sept dix

${displaystyle mu ={frac {988.7}{10}}}$

?? = 98, 87

${style d`affichage mu =98.87}$

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 4

4. Calculer les valeurs d`erreur individuelles. Dans la deuxième colonne de votre tableau, vous devez entrer les valeurs d`erreur pour chaque valeur de données. L`erreur est la différence entre la lecture et la moyenne.

Pour l`ensemble de données donné, soustrayez la moyenne, 98,87, de chaque valeur mesurée, et remplissez la deuxième colonne avec les résultats. Ces dix calculs se présentent comme suit :

99, 0 - 98, 87 = 0, 13

${style d`affichage 99.0-98.87=0.13}$

98, 6 - 98, 87 = - 0, 27

${style d`affichage 98.6-98.87=-0.27}$

98, 5 - 98, 87 = - 0, 37

${style d`affichage 98.5-98.87=-0.37}$

101, 1 - 98, 87 = 2, 23

${style d`affichage 101.1-98.87=2.23}$

98, 3 - 98, 87 = - 0, 57

${style d`affichage 98.3-98.87=-0.57}$

98, 6 - 98, 87 = - 0, 27

${style d`affichage 98.6-98.87=-0.27}$

97, 9 - 98, 87 = - 0, 97

${style d`affichage 97.9-98.87=-0.97}$

98, 4 - 98, 87 = - 0, 47

${style d`affichage 98.4-98.87=-0.47}$

99, 2 - 98, 87 = 0, 33

${style d`affichage 99.2-98.87=0.33}$

99, 1 - 98, 87 = 0, 23

${style d`affichage 99.1-98.87=0.23}$

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 5

5. Calculer l`ESS. Dans la troisième colonne du tableau, trouvez le carré de chacune des valeurs résultantes dans la colonne du milieu. Ceux-ci représentent les carrés de l`écart par rapport à la moyenne pour chaque valeur de données mesurée.

Pour chaque valeur de la colonne du milieu, utilisez une calculatrice pour calculer le carré. Enregistrez les résultats dans la troisième colonne, comme suit :

0, 13 2 = 0, 0169

${style d`affichage 0,13^{2}=0,0169}$

(- 0, 27) 2 = 0, 0729

${style d`affichage (-0,27)^{2}=0,0729}$

(- 0, 37) 2 = 0, 1369

${style d`affichage (-0,37)^{2}=0,1369}$

2, 23 2 = 4, 9729

${style d`affichage 2.23^{2}=4.9729}$

(- 0, 57) 2 = 0, 3249

${style d`affichage (-0,57)^{2}=0,3249}$

(- 0, 27) 2 = 0, 0729

${style d`affichage (-0,27)^{2}=0,0729}$

(- 0, 97) 2 = 0, 9409

${style d`affichage (-0,97)^{2}=0,9409}$

(- 0, 47) 2 = 0, 2209

${style d`affichage (-0.47)^{2}=0.2209}$

0, 33 2 = 0, 1089

${style d`affichage 0.33^{2}=0.1089}$

0, 23 2 = 0, 0529

${style d`affichage 0,23^{2}=0,0529}$

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 6

6. Additionner les carrés des erreurs ensemble. La dernière étape consiste à trouver la somme des valeurs dans la troisième colonne. Le résultat souhaité est le SSE, ou la somme des carrés des erreurs.

Pour cet ensemble de données, le SSE est calculé en additionnant les dix valeurs de la troisième colonne :

s s E = 6, 921

${style d`affichage SSE=6.921}$

Méthode 2 sur 3: Créer une feuille de calcul Excel pour calculer le SSE

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 7

1. Étiqueter les colonnes de la feuille de calcul. Vous créez un tableau avec trois colonnes dans Excel, avec les mêmes trois en-têtes que ci-dessus.

Dans la cellule A1, tapez « Valeur » comme titre.
Dans la case B1, tapez « Déviation » comme titre.
Dans la case C1, tapez « Déviation au carré » comme titre.

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 8

2. Entrez vos coordonnées. Dans la première colonne, vous devez entrer les valeurs de vos mesures. Si l`ensemble est petit, vous pouvez facilement le saisir à la main. Si vous avez un jeu de données volumineux, vous devrez peut-être copier et coller les données dans la colonne.

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 9

3. Déterminer la moyenne des points de données. Excel a une fonction qui calcule la moyenne pour vous. Dans une cellule vide sous votre tableau de données (peu importe la cellule que vous choisissez), saisissez :

=Moyenne(A2:___)

Ne tapez pas d`espace vide. Remplissez cet espace avec le nom de la cellule de votre dernier point de données. Par exemple, si vous avez 100 points de données, vous utiliserez la fonction :

=Moyenne(A2:A101)

Cette fonction contient les données des cellules A2 à A101, car la ligne du haut contient les en-têtes de colonne.

Lorsque vous appuyez sur Entrée ou cliquez sur une autre cellule du tableau, la nouvelle cellule programmée est automatiquement remplie avec la moyenne de vos valeurs de données.

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 10

4. Entrez dans la fonction de mesure d`erreur. Dans la première cellule vide de la colonne « Déviation », vous devez entrer une fonction pour calculer la différence entre chaque point de données et la moyenne. Pour ce faire, utilisez le nom de la cellule où se trouve la moyenne. Supposons que vous utilisiez la cellule A104 pour l`instant.

La fonction de calcul d`erreur, que vous saisissez dans la cellule B2, est :

=A2-$A$104. Les signes dollar sont nécessaires pour vous assurer de verrouiller la case A104 pour chaque calcul.

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 11

5. Remplissez la fonction pour les erreurs au carré. Dans la troisième colonne, vous pouvez demander à Excel de calculer le carré souhaité.

Dans la cellule C2, entrez la fonction suivante :

=B2^2

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 12

6. Copiez les fonctions pour remplir tout le tableau. Après avoir entré les fonctions dans la cellule supérieure de chaque colonne, respectivement B2 et C2, vous devez remplir tout le tableau. Vous pouvez retaper la fonction dans chaque ligne du tableau, mais cela prendrait beaucoup trop de temps. À l`aide de votre souris, mettez en surbrillance les cellules B2 et C2 ensemble, et sans relâcher le bouton de la souris, faites glisser vers la cellule du bas de chaque colonne.

En supposant que vous ayez 100 points de données dans votre tableau, faites glisser votre souris vers les cellules B101 et C101.

Lorsque vous relâchez le bouton de la souris, les formules sont copiées dans toutes les cellules du tableau. Le tableau doit être automatiquement rempli avec les valeurs calculées.

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 13

sept. Trouver l`ESS. La colonne C de votre tableau contient toutes les valeurs d`erreur au carré. La dernière étape consiste à laisser Excel calculer la somme de ces valeurs.

Dans une cellule sous le tableau, probablement C102 dans cet exemple, entrez la fonction suivante :

=Somme(C2:C101)

Cliquer sur Entrée ou cliquer dans une autre cellule du tableau vous donnera la valeur SSE de vos données.

Méthode 3 sur 3: Relier l`ESS à d`autres données statistiques

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 14

1. Calculer l`écart de la SSE. Trouver le SSE pour un ensemble de données est généralement un élément constitutif pour trouver d`autres valeurs plus utiles. Le premier d`entre eux est la variance. La variance est une mesure qui indique de combien les données mesurées s`écartent de la moyenne. C`est en fait la moyenne des différences au carré par rapport à la moyenne.

Puisque le SSE est la somme des erreurs au carré, vous pouvez trouver la moyenne (c`est la variance) simplement en divisant par le nombre de valeurs. Cependant, si vous calculez la variance d`un ensemble d`échantillons plutôt que d`une population entière, vous divisez la variance par (n-1) au lieu de n. Alors:

Variance = SSE/n, si vous calculez la variance d`une population entière.
Variance = SSE/(n-1), si vous calculez la variance d`un échantillon de données.

Pour le problème d`échantillon de la température des patients, nous pouvons supposer que 10 patients ne constituent qu`un échantillon. Par conséquent, la variance est alors calculée comme suit :

Variance = ESS (m - 1)

${displaystyle {text{Variation}}={frac {text{SSE}}{(n-1)}}}$

Variance = 6, 921 9

${displaystyle {text{Variation}}={frac {6,921}{9}}}$

Variance = 0, 769

${displaystyle {text{Variation}}=0.769}$

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 15

2. Calculer l`écart type de l`ESS. L`écart type est une valeur couramment utilisée qui indique de combien les valeurs d`un ensemble de données s`écartent de la moyenne. L`écart type est la racine carrée de la variance. Notez que la variance est la moyenne des mesures d`erreur au carré.

Par conséquent, après avoir calculé le SSE, vous pouvez trouver l`écart type comme suit :

écart-type = \sqrt{ESS} m - 1

${displaystyle {text{Déviation standard}}={sqrt {frac {text{SSE}}{n-1}}}}$

Pour l`échantillon des mesures de température, vous pouvez trouver l`écart type comme suit :

écart-type = \sqrt{ESS} m - 1

${displaystyle {text{Déviation standard}}={sqrt {frac {text{SSE}}{n-1}}}}$

écart-type = \sqrt{\frac{6.921}{9}}

${displaystyle {text{Déviation standard}}={sqrt {frac {text{6,921}}{9}}}}$

écart-type = \sqrt{0, 769}

${displaystyle {text{Déviation standard}}={sqrt {0.769}}}$

écart-type = 0, 877

${displaystyle {text{Déviation standard}}=0.877}$

Image intitulée Calculer la somme des carrés pour l`erreur (SSE) Étape 16

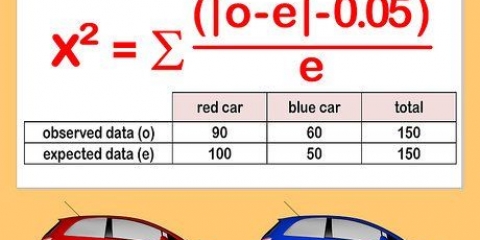
3. Utiliser SSE pour déterminer la covariance. Cet article s`est concentré sur les ensembles de données qui ne mesurent qu`une seule valeur à la fois. Cependant, dans de nombreuses études, vous pouvez comparer deux valeurs distinctes. Par exemple, vous voulez savoir comment ces deux valeurs sont liées l`une à l`autre, pas seulement à la moyenne de l`ensemble de données. Cette valeur est la covariance.

Les calculs de covariance sont trop détaillés pour être décrits ici, sauf pour noter que vous utiliserez le SSE pour chaque type de données, puis le comparerez. Pour une description plus détaillée de la covariance et des calculs impliqués, voir trouver des articles sur ce sujet sur wikiHow.

Comme exemple d`utilisation de la covariance, vous pouvez comparer l`âge des patients dans une étude médicale avec l`efficacité d`un médicament pour abaisser la température fébrile. Ensuite, vous avez un ensemble de données d`âges et un deuxième ensemble de données de températures. Vous trouvez ensuite le SSE pour chaque ensemble de données, et à partir de là la variance, les écarts types et la covariance.