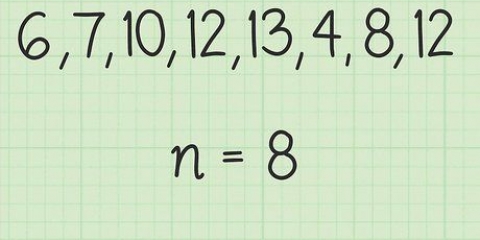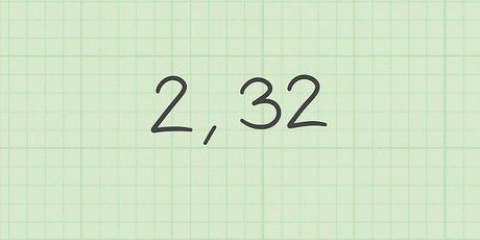Calcul d'une erreur relative : 9 étapes (avec photos)

Teneur

Pas
- Méthode 1 sur 2: Calcul de l`erreur absolue
- Méthode 2 sur 2: Calculer l`erreur relative
Des astuces
Mises en garde

L`erreur absolue est le degré réel auquel une valeur est incorrecte, ou incorrecte, dans une mesure. Une erreur relative compare l`erreur absolue avec l`amplitude de ce que vous vouliez mesurer. Pour calculer l`erreur relative, vous devez également calculer l`erreur absolue. Si vous vouliez mesurer quelque chose de 12 cm et que votre mesure est sortie à 6 cm, l`erreur relative est très grande. Mais si vous vouliez mesurer quelque chose de 120 cm et vous en écarter de 6 cm, l`erreur relative est beaucoup plus petite -- bien que l`amplitude de l`erreur absolue, 6 cm, n`ait pas changé.

Pas

Méthode 1 sur 2: Calcul de l`erreur absolue

Image intitulée Calculer l`erreur relative Étape 1

1. À une valeur attendue donnée, soustrayez la valeur que vous avez obtenue de la valeur attendue pour obtenir l`erreur absolue. Une valeur attendue est généralement donnée dans les tests et les travaux pratiques. En bref, il s`agit de la mesure standard la plus précise, généralement pour les équations ou les réactions générales. Vous pouvez comparer vos propres résultats pour découvrir l`erreur absolue, qui mesure de combien vos lectures s`écartent des résultats attendus. Pour ce faire, soustrayez la valeur mesurée de la valeur attendue. Même si le résultat est négatif, tu le rends positif. C`est l`erreur absolue!

Exemple: Vous voulez savoir avec quelle précision vous pouvez estimer les distances en comptant les pas. Vous comptez vos pas d`un arbre à l`autre et suppose qu`ils sont à 18 mètres l`un de l`autre. C`est la valeur expérimentale. Ensuite, vous revenez avec un long ruban à mesurer pour mesurer la distance exacte, montrant que les arbres sont distants de 20 mètres. C`est la "vraie" valeur. Votre erreur absolue est 20 - 18=2 mètres.

Image intitulée Calculer l`erreur relative, étape 2

2. Alternativement, lorsque vous mesurez quelque chose, vous pouvez également supposer que l`erreur absolue est la plus petite unité de mesure dont vous disposez. Par exemple, si vous mesurez quelque chose avec un ruban à mesurer, la plus petite unité indiquée sur la jauge est 1 millimètre (mm). Vous savez donc maintenant que votre mesure est précise à + ou - 1 mm. L`erreur absolue est alors de 1 mm.

Cela fonctionne pour n`importe quel système de mesure. De nombreux outils scientifiques, tels qu`une pipette de précision et un équipement de mesure, ont souvent l`erreur absolue comme étiquette sur le côté (comme `+/-___`).

Image intitulée Calculer l`erreur relative Étape 3

3. Ajoutez toujours les unités que vous voulez. Supposons que votre erreur absolue soit « 2 mètres ». Cela indique quelle est votre marge d`erreur. Mais si vous écrivez simplement que votre erreur est `2`, cela ne dit rien au lecteur. Utilisez les mêmes unités que celles de vos mesures.

Image intitulée Calculer l`erreur relative Étape 4

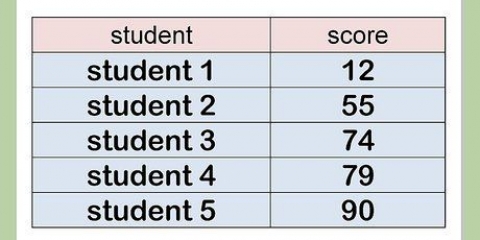
4. Entraînez-vous avec différents exemples. La meilleure façon d`apprendre à calculer la marge d`erreur est de s`entraîner. Essayez les problèmes suivants et recherchez les deux points (:) pour la réponse.

Janet étudie les réactions chimiques. Après mélange et appariement, son tube à essai contient 32 grammes de substrat. La valeur acceptée pour son expérience était de 34 grammes. Son erreur absolue est : +/-2 grammes

Kees teste des réactions chimiques. Il faut 10 ml de gouttes d`eau pour provoquer une réaction, mais sa pipette dit que c`est " +/- 0,5 ml ". L`erreur absolue dans ses mesures devient : +/- 0,5 ml

Image intitulée Calculer l`erreur relative Étape 5

5. Comprendre la cause de l`erreur et comment la réduire. Aucune étude scientifique n`est jamais complètement exempte d`erreurs - même les articles et les découvertes lauréats du prix Nobel ont une marge d`erreur ou d`erreur quelque part. Pourtant, il est essentiel d`éviter les erreurs en découvrant ce qui les provoque :

Les erreurs humaines sont les erreurs les plus courantes. Cela inclut des lectures médiocres, des hypothèses invalides ou des erreurs de laboratoire.

Pertes occasionnelles d`énergie/matériel, telles que du liquide résiduel dans la tasse après le versement, des changements de température dus à l`environnement, etc.

Équipement défectueux utilisé pour la mesure ou les études, comme les mesures de haute précision des brûleurs qui dégagent une chaleur inégale.

Méthode 2 sur 2: Calculer l`erreur relative

Image intitulée Calculer l`erreur relative Étape 6

1. Divisez l`erreur absolue par la taille réelle de l`élément en question pour trouver l`erreur relative. Le résultat est l`erreur relative.

Notez que dans la plupart des cas, l`unité de mesure de l`erreur absolue sera la même que l`unité de mesure de la vraie valeur, et ces unités s`annuleront. Cela donne l`erreur relative sans aucune unité de mesure.
L`équation simple suivante vous indique l`ampleur de votre écart par rapport à la lecture totale. Une erreur relative faible est bien sûr souhaitable. On continue avec l`exemple de la distance entre deux arbres :
L`erreur absolue était 2 mètres et la valeur réelle était 20 mètres.
$2 m 20 m$ ${frac{2m}{20m}}$
Erreur relative $= 0, 1$ ${style d`affichage =0.1}$

Image intitulée Calculer l`erreur relative Étape 7

2. Multipliez la réponse par 100 pour obtenir le pourcentage (plus facile à comprendre). Laissez l`erreur relative sous forme de fraction, complétez la division pour pouvoir l`afficher en décimal, ou multipliez la décimale résultante par 100 pour obtenir votre réponse en pourcentage. Cela vous indique l`écart par rapport à la dernière lecture exprimée en pourcentage. Si vous mesurez une distance de 200 mètres et que la mesure s`écarte de 2 mètres, le taux d`erreur sera bien inférieur à un écart de 2 mètres sur une distance de 20 mètres. L`erreur est un plus petit pourcentage de la lecture totale.

2 m 20 m = 0, 1

${style d`affichage {frac {2}m}{20m}}=0.1}$

$0, 1 * 100 = dix %$ ${style d`affichage 0.1*100=10%}$ Erreur relative.

3. Calculer l`erreur relative à la fois en combinant le numérateur de la fraction avec l`équation de l`erreur absolue. Une fois que vous comprenez la différence entre l`erreur absolue et relative, il n`y a vraiment aucune raison de tout faire séparément. Remplacez l`équation de l`erreur absolue par le nombre réel. Notez que les barres verticales représentent la valeur absolue du nombre, ce qui signifie que ce nombre est toujours positif.

Erreur relative

= | g e m e t e m - w e r k e je je j k | w e r k e je je j k

${displaystyle ={frac {|mathrm {mesuré} -mathrm {réel} |}{mathrm {réel} }}}$

Multipliez le tout par 100 pour le taux d`erreur relatif.

Image intitulée Calculer l`erreur relative Étape 9

4. Toujours indiquer les unités comme contexte. Faites savoir au lecteur quelles unités vous avez utilisées pour la mesure. Cependant, l`erreur relative n`utilise pas d`unités de mesure. Elle est exprimée en fraction ou en pourcentage, comme une erreur relative de 10 %.

Des astuces

Assurez-vous que votre valeur expérimentale et votre valeur réelle sont toutes deux exprimées dans la même unité de mesure. Par exemple, si votre valeur expérimentale est en centimètres, mais que votre valeur réelle est en millimètres, vous devez convertir l`une de ces unités en l`autre.