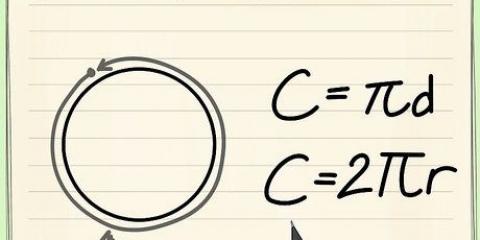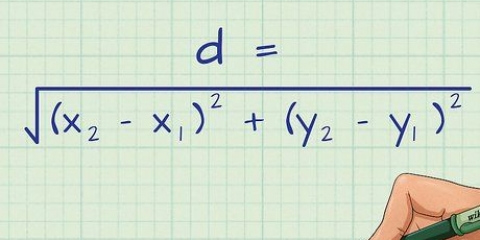Calcul de la longueur de l'arc : 10 étapes (avec photos)

Teneur

Pas
- Méthode 1 sur 2: Utilisation de l`angle au centre en degrés
- Méthode 2 sur 2: Utilisation de l`angle au centre en radians
Des astuces

Un arc est n`importe quelle partie de la circonférence d`un cercle. La longueur de l`arc est la distance d`un point d`extrémité de l`arc à l`autre. Le calcul de la longueur de l`arc nécessite une certaine connaissance de la géométrie d`un cercle. Étant donné que l`arc fait partie du périmètre, vous pouvez facilement savoir quelle est la longueur de l`arc si vous savez quelle partie des 360 degrés est l`angle central de l`arc.

Pas

Méthode 1 sur 2: Utilisation de l`angle au centre en degrés

1. Ecrire la formule de la longueur de l`arc. La formule est

longueur de l`arc = 2 ?? (r) (\frac{??}{360})

${text{arclength}}=2pi (r)({frac{theta }{360}})$ , par lequel

r

$r$ est égal au rayon du cercle et

??

$theta$ est égal à l`amplitude de l`angle de l`arc central, en degrés.

2. Remplacer la longueur du rayon du cercle dans la formule. Cette information doit être donnée, ou vous devez pouvoir la mesurer. Assurez-vous d`entrer la longueur du rayon pour la variable

r

$r$ .

Par exemple, si le rayon du cercle est de 10 cm, la formule ressemblerait à ceci :

longueur de l`arc = 2 ?? (dix) (\frac{??}{360})

${text{arc length}}=2pi (10)({frac{theta }{360}})$ .

3. Remplacez la valeur de l`angle de l`arc central dans la formule. Cette information doit être donnée, ou vous devez pouvoir la mesurer. Assurez-vous de travailler avec des degrés (pas des radians) lors de l`application de cette formule. Remplacez l`angle de l`arc central par

??

$theta$ dans la formule.

Par exemple, si l`angle de l`arc central est de 135 degrés, la formule ressemblerait à ceci :

longueur de l`arc = 2 ?? (dix) (\frac{135}{360})

${text{arclength}}=2pi (10)({frac{135}{360}})$ .

4. Multipliez le rayon par 2??{style d`affichage 2pi } $2pi$ . Si vous n`utilisez pas de calculatrice, vous pouvez utiliser l`approximation

?? = 3, 14

$pi =3.14$ utiliser pour les calculs. Réécrivez la formule en utilisant cette nouvelle valeur (circonférence du cercle).

Par exemple:

2 ?? (dix) (\frac{135}{360})

$2pi (10)({frac{135}{360}})$

2 (3, 14) (dix) (\frac{135}{360})

$2(3,14)(10)({frac{135}{360}})$

(62, 8) (\frac{135}{360})

$(62,8)({frac{135}{360}})$

5. Divisez l`angle de l`arc central par 360. Puisqu`un cercle a un total de 360 degrés, ce calcul vous donnera la partie du cercle complet qui est égale à ce segment. Avec cette information, vous pouvez trouver la partie de la circonférence qui représente la longueur de l`arc.

Par exemple:

(62, 8) (\frac{135}{360})

$(62,8)({frac{135}{360}})$

(62, 8) (0, 375)

$(62,8) (0,375)$

6. Multipliez les deux nombres ensemble. Le résultat est la longueur de l`arc.

Par exemple:

(62, 8) (0, 375)

$(62,8) (0,375)$

23, 55

$23.55$
Ainsi, la longueur de l`arc de cercle avec un rayon de 10 cm et un angle au centre de 135 degrés, est d`environ 23,55 cm.

Méthode 2 sur 2: Utilisation de l`angle au centre en radians

1. Ecrire la formule de la longueur de l`arc. La formule est

longueur de l`arc = ?? (r)

${text{longueur de l`arc}}=theta (r)$ , où

??

$theta$ et est égal à la valeur de l`angle de l`arc central en radians, et

r

$r$ est égal à la longueur du rayon du cercle.

2. Remplacer la longueur du rayon du cercle dans la formule. Vous avez besoin de la longueur du rayon pour cette méthode. Assurez-vous d`utiliser la longueur du rayon comme valeur pour la variable

r

$r$ .

Par exemple, si le rayon du cercle est de 10 cm, la formule ressemblerait à ceci :

longueur de l`arc = ?? (dix)

${text{longueur de l`arc}}=theta (10)$ .

3. Remplacez la valeur de l`angle de l`arc central dans la formule. Cette information doit être donnée en radians. Si la valeur de l`angle est donnée en degrés, vous ne pouvez pas utiliser cette méthode.

Par exemple, si l`angle de l`arc central est de 2,36 radians, la formule ressemblerait à ceci :

longueur de l`arc = 2, 36 (dix)

${text{longueur de l`arc}}=2.36(10)$ .

4. Multiplier le rayon par la valeur du radian. Le produit est la longueur de l`arc.

Par exemple:

2, 36 (dix)

$2.36(10)$

= 23, 6

$=23,6$
Donc la longueur de l`arc de cercle avec un rayon de 10 cm et un angle au centre de 2,36 radians, est d`environ 23,6 cm.

Des astuces

Si vous connaissez le diamètre du cercle, vous pouvez également calculer la longueur de l`arc. Les formules pour trouver la longueur de l`arc utilisent le rayon du cercle. Puisque le rayon est la moitié d`un cercle, vous pouvez trouver le rayon en divisant le diamètre par 2. Par exemple, si le diamètre d`un cercle est de 14 cm, divisez 14 par 2 pour trouver le rayon :
$14 ?? 2 = sept$ $14div 2=7$ .
Donc le rayon du cercle est de 7 cm.