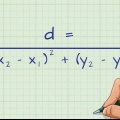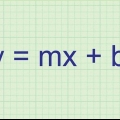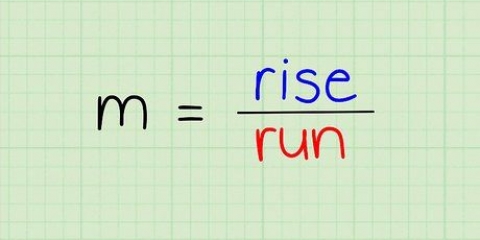Comment calculer la pente et les intersections d'une ligne

Teneur

La pente d`une ligne mesure la pente de la ligne.Vous pouvez également dire que c`est la distance sur l`axe des y par rapport à la distance sur l`axe des x - c`est-à-dire de combien la ligne monte verticalement par rapport à combien elle augmente horizontalement. Être capable de trouver la pente d`une ligne, ou d`utiliser la pente pour trouver des points sur la ligne, est une compétence importante utilisée en mathématiques, en économie, en sciences, en comptabilité/finance et dans d`autres domaines.

Pas

Méthode 1 sur 4: Utiliser un graphique pour trouver la pente

Image intitulée Calculer la pente et les interceptions d`une ligne Étape 1

1. Choisissez deux points sur la ligne. Dessinez des points sur le graphique pour représenter ces points et notez leurs coordonnées.

Lorsque vous dessinez des points, n`oubliez pas de mentionner d`abord la coordonnée x puis la coordonnée y.
Par exemple : vous pouvez choisir les points (-3, -2) et (5, 4).

Image intitulée Calculer la pente et les interceptions d`une ligne Étape 2

2. Trouver la montée entre les deux points. Pour ce faire, vous devez comparer la différence en y des deux points. Commencez par le premier point, le point le plus à gauche sur le graphique, et comptez jusqu`à ce que vous arriviez à la coordonnée y du deuxième point.

L`augmentation peut être positive ou négative ; c`est-à-dire que vous devez compter vers le haut ou peut-être vers le bas pour le trouver. Si la ligne se déplace vers le haut et vers la droite, la montée est positive. Si la ligne se déplace vers le bas et vers la droite, la montée est négative.

Par exemple, si la coordonnée y du premier point est (-2) et la coordonnée y du deuxième point est (4), alors vous ajoutez six points et la montée est de 6.

Image intitulée Calculer la pente et les interceptions d`une ligne Étape 3

3. Déterminer la distance horizontale entre les deux points. Pour ce faire, vous devez comparer la différence des valeurs x des deux points. Commencez par le premier point, le point le plus à gauche du graphique, et comptez jusqu`à ce que vous arriviez à la coordonnée x du deuxième point.

La distance horizontale est toujours positive ; c`est-à-dire que vous ne pouvez compter que de gauche à droite, jamais de droite à gauche.

Par exemple, si la coordonnée x du premier point est (-3) et la coordonnée x du deuxième point est (5), alors vous compteriez une distance de 8.

Image intitulée Calculer la pente et les interceptions d`une ligne Étape 4

4. Faire un rapport y/x pour trouver la pente. La pente est généralement une fraction, mais peut aussi être un nombre entier.

Par exemple, si la montée est de 6 et la descente est de 8, alors votre pente est

\frac{6}{8}

${style d`affichage {frac {6}{8}}}$ , qui peut être simplifié en

\frac{3}{4}

${frac{3}{4}}$ .

Méthode 2 sur 4: Utiliser deux points donnés pour trouver la pente

Image intitulée Calculer la pente et les interceptions d`une ligne Étape 5

1. Écrivez la formule suivante :

m = oui 2 - {oui}_{1} X 2 - X_{1}

${displaystyle m={frac {y_{2}-y_{1}}{x_{2}-x_{1}}}}$ . Dans cette formule, `m` est la pente,

(X 1, {oui}_{1})

$(x_{{1}},y_{{1}})$ sont les coordonnées du premier point,

(X 2, {oui}_{2})

$(x_{{2}},y_{{2}})$ sont les coordonnées du deuxième point.

Rappelez-vous que la pente est égale à $\frac{oui}{X}$ ${frac{y}{x}}$ . Vous utilisez cette formule pour trouver la variation de y (élévation) par rapport à la variation de x (distance).

Image intitulée Calculer la pente et les interceptions d`une ligne Étape 6

2. Mettez les coordonnées x et y dans la formule. Assurez-vous d`avoir les coordonnées du premier point (

(X 1, {oui}_{1})

$(x_{{1}},y_{{1}})$ ) et le deuxième point (

(X 2, {oui}_{2})

$(x_{{2}},y_{{2}})$ ) aux bons endroits dans la formule, sinon vous ne calculerez pas la bonne pente.

Par exemple, étant donné les points (-3, -2) et (5, 4), votre formule ressemblera à ceci :

m = 4 - (- 2) 5 - (- 3)

${displaystyle m={frac {4-(-2)}{5-(-3)}}}$ .

Image intitulée Calculer la pente et les interceptions d`une ligne Étape 7

3. Compléter le calcul et simplifier si possible. Cela vous donnera la pente sous forme de fraction ou d`entier.

Par exemple : avec une pente

m = 4 - (- 2) 5 - (- 3)

${displaystyle m={frac {4-(-2)}{5-(-3)}}}$ est-ce que tu calcules

4 - (- 2) = 6

${style d`affichage 4-(-2)=6}$ au numérateur ((n`oubliez pas d`ajouter lors de la soustraction d`un nombre négatif) et

5 - (- 3) = 8

${style d`affichage 5-(-3)=8}$ au dénominateur. tu as simplifié

\frac{6}{8}

${style d`affichage {frac {6}{8}}}$ puis à

\frac{3}{4}

${frac{3}{4}}$ , Et ainsi

m = \frac{3}{4}

${displaystyle m={frac {3}{4}}}$ .

Méthode 3 sur 4: Détermination de l`intersection avec l`axe des y, étant donné la pente et un point

Image intitulée Calculer la pente et les interceptions d`une ligne Étape 8

1. Définir la formule oui=mX+b{style d`affichage y=mx+b} ${style d`affichage y=mx+b}$ au. Dans la formule, y est la coordonnée y de n`importe quel point sur la ligne droite, m est la pente, x est la coordonnée x de n`importe quel point sur la ligne et b est l`intersection avec l`axe des y.

$oui = m X + b$ $y=mx+b$ est l`équation d`une droite.
L`intersection avec l`axe des y est le point où la ligne croise l`axe des y.

CONSEIL D`EXPERT

Grace Imson, MA

Professeur de mathématiques au City College de San FranciscoGrace Imson est professeur de mathématiques avec plus de 40 ans d`expérience. Elle enseigne actuellement les mathématiques au City College de San Francisco et a précédemment fait partie de la faculté de mathématiques de l`Université de Saint Louis. Grace a enseigné les mathématiques à l`école primaire, secondaire et collégiale. Elle est titulaire d`une maîtrise en sciences de l`éducation avec une spécialisation en gestion et supervision scolaires de l`Université de Saint Louis.

Grace Imson, MA
Professeur de mathématiques au City College de San Francisco

Notre expert explique : » Si vous avez la pente et un point, vous en tenez compte dans l`équation de la ligne. Dans y = mx + b, m est la pente et les coordonnées du point contiendront à la fois x et y. Ensuite, résolvez pour b pour trouver l`intersection avec l`axe des y.

Image intitulée Calculer la pente et les interceptions d`une ligne Step 9

2. Traiter la pente et les coordonnées d`un point de la ligne. Rappelez-vous que la pente est égale à la montée sur la distance horizontale. Si vous avez besoin d`aide pour trouver la pente, consultez les instructions ci-dessus.

Par exemple : si la pente est égale à

\frac{3}{4}

${frac{3}{4}}$ , et un point sur la ligne est (5.4), alors la formule ressemble à ceci :

4 = \frac{3}{4} (5) + b

${displaystyle 4={frac {3}{4}}(5)+b}$ .

Image intitulée Calculer la pente et les interceptions d`une ligne Step 10

3. Résoudre l`équation de b. Multipliez d`abord la pente et la coordonnée x. Soustraire ce nombre des deux côtés pour résoudre pour b.

Dans l`exemple de problème, l`équation devient

4 = 3 \frac{3}{4} + b

${displaystyle 4=3{frac {3}{4}}+b}$ . Si vous

3 \frac{3}{4}

${style d`affichage 3{frac {3}{4}}}$ soustrait des deux côtés, vous vous retrouvez avec

\frac{1}{4} = b

${displaystyle {frac {1}{4}}=b}$ . Donc l`intersection avec l`axe des y est égale à

\frac{1}{4}

${frac{1}{4}}$ .

Image intitulée Calculer la pente et les interceptions d`une ligne Step 11

4. Vérifie ton travail. Tracez le point connu sur un graphique, puis tracez une ligne en utilisant la pente (la pente). Pour trouver l`intersection avec l`axe des y, trouvez le point où la ligne coupe l`axe des y.

Par exemple : si la pente

\frac{3}{4}

${frac{3}{4}}$ est, et un point est (5.4), puis dessinez un point vers le haut (5.4), puis dessinez d`autres points le long de la ligne en allant quatre vers la gauche et trois vers le bas. Si vous tracez une ligne passant par les points, la ligne doit couper l`axe des y juste au-dessus de la coordonnée (0,0).

Méthode 4 sur 4: Détermination de l`intersection avec l`axe des x, étant donné la pente et l`intersection avec l`axe des y

Image intitulée Calculer la pente et les interceptions d`une ligne Step 12

$oui = m X + b$ $y=mx+b$ est l`équation d`une droite.
L`intersection avec l`axe des x est le point où la ligne croise l`axe des x.

Image intitulée Calculer la pente et les interceptions d`une ligne Step 13

2. Appliquer la pente et l`intersection avec l`axe des y à la formule. Rappelez-vous que la pente est égale à la montée sur la distance horizontale. Si vous avez besoin d`aide pour trouver la pente, consultez les instructions ci-dessus.

Par exemple : la pente est

\frac{3}{4}

${frac{3}{4}}$ , et l`intersection avec l`axe des y est

\frac{1}{4}

${frac{1}{4}}$ , donc la formule ressemblera à ceci:

oui = \frac{3}{4} X + \frac{1}{4}

${displaystyle y={frac {3}{4}}x+{frac {1}{4}}}$ .

Image intitulée Calculer la pente et les interceptions d`une ligne Step 14

3. Mettre y à 0.Vous cherchez l`intersection avec l`axe des x, le point où la ligne croise l`axe des x. À ce stade, la coordonnée y sera zéro. Donc, si nous définissons y à 0 et résolvons la coordonnée x correspondante, nous trouvons le point (x, 0), qui est l`intersection avec l`axe des x.

Dans l`exemple de problème, l`équation devient

0 = \frac{3}{4} X + \frac{1}{4}

${displaystyle 0={frac {3}{4}}x+{frac {1}{4}}}$ .

Image intitulée Calculer la pente et les interceptions d`une ligne Step 15

4. Complétez l`équation en résolvant pour x. Soustraire d`abord l`intersection avec l`axe des y des deux côtés. Puis diviser les deux côtés par la pente.

Dans l`exemple de problème, l`équation devient

- 1 4 = \frac{3}{4} X

${displaystyle {frac {-1}{4}}={frac {3}{4}}x}$ . Diviser les deux côtés

\frac{3}{4}

${frac{3}{4}}$ , et vous obtenez

- 4 12 = X

${style d`affichage {frac {-4}{12}}=x}$ . Ceci est simplifié à

- 1 3 = X

${style d`affichage {frac {-1}{3}}=x}$ . L`intersection avec l`axe des x est donc

(- 1 3, 0)

${style d`affichage ({frac {-1}{3}},0)}$ . Ainsi

- 1 3

${style d`affichage {frac {-1}{3}}}$ .

Image intitulée Calculer la pente et les interceptions d`une ligne Step 16

5. Vérifie ton travail. Tracez le graphique de l`intersection avec l`axe des y, puis tracez une ligne avec la pente. Pour trouver l`intersection avec l`axe des x, trouvez le point où la ligne coupe l`axe des x.

Par exemple : si la pente

\frac{3}{4}

${frac{3}{4}}$ est , et l`intersection avec l`axe des y

(0, \frac{1}{4})

${style d`affichage (0,{frac {1}{4}})}$ , puis dessine le point

(0, \frac{1}{4})

${style d`affichage (0,{frac {1}{4}})}$ , puis dessinez d`autres points le long de la ligne en comptant 4 vers la gauche et 3 vers le bas, et 3 vers la droite et 4 vers le haut. Si vous tracez une ligne passant par les points, vous verrez que la ligne traverse l`axe des x juste à gauche de la coordonnée (0,0).