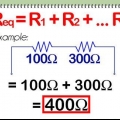
Par exemple, un circuit en série a une résistance de 2 (ohms), 5 et 7. La résistance totale du circuit est de 2 + 5 + 7 = 14 Ω. 
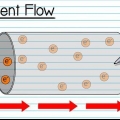
Le courant d`un circuit série est le même en tous points du circuit. Si vous savez quel est le courant à un certain point, vous pouvez utiliser cette valeur dans l`équation. La tension totale est égale à la tension de l`alimentation (la batterie). C `est ne pas égale à la tension aux bornes d`un composant. 
Par exemple, un circuit en série est alimenté par une batterie de 12 volts, et le courant est égal à 8 ampères. La résistance totale à travers le circuit est alors Rt = 12 volts / 8 ampères = 1,5 ohms. 

Par exemple, un circuit parallèle a trois branches, avec des résistances 10 , 2 et 1.
Utilisez la formule et résoudre pour Rt:
et résoudre pour Rt:
Convertir des fractions au dénominateur commun :

Multiplier les deux côtés par Rt: 1 = 1.6Rt
Rt = 1 / 1.6 = 0.625 ??. 
Dans un circuit parallèle, la tension aux bornes d`une branche est égale à la tension totale aux bornes du circuit. Tant que vous connaissez la tension sur une branche, vous pouvez continuer. La tension totale est également égale à la tension de la source d`alimentation du circuit, telle qu`une batterie. Dans un circuit parallèle, le courant à travers chaque branche peut être différent. tu as le le total nécessite du courant, sinon vous ne pouvez pas savoir quelle est la résistance totale. 
Par exemple, un circuit parallèle a une tension de 9 volts et un courant de 3 ampères. La résistance totale Rt = 9 volts / 3 ampères = 3. 
Dans les applications pratiques, cela signifie généralement qu`une résistance cesse de fonctionner ou est contournée (court-circuitée), ce qui permet au courant plus élevé d`endommager d`autres parties du circuit. 

L`exemple de circuit a deux branches avec la résistance R1 = 5 et R2 = 3.


 ??
?? 
Dans l`exemple ci-dessus, vous pouvez ignorer les deux branches et les considérer comme une seule résistance de 1,875 . 
Le schéma simplifié a une résistance de 1 Ω, 1.Résistance de 5 et la section de 1,875 que vous venez de calculer. Ils sont tous connectés en série, donc  ??.
??. 


P = VI (puissance = tension x courant) La loi d`Ohm nous dit que V = IR. Remplacez IR par V dans la première formule : P = (IR)I = IR. Réorganiser pour déterminer la résistance : R = P / I. Dans un circuit en série, le courant à travers un composant est le même que le courant total. Ceci ne s`applique pas à un circuit parallèle. 
P = VI Réorganiser la loi d`Ohm en I : I = V / R. Remplacez V / R par I dans la formule de puissance : P = V(V/R) = V/R. Réorganisez la formule pour résoudre la résistance : R = V/P. Dans un circuit parallèle, la tension aux bornes d`une branche est la même que la tension totale. Ce n`est pas vrai pour un circuit en série : la tension aux bornes d`un composant n`est pas égale à la tension totale.
Calcul de la résistance totale dans un circuit
Teneur
Il existe deux façons de connecter des composants électriques. Les circuits série sont des composants connectés les uns après les autres, tandis que dans un circuit parallèle, les composants sont connectés dans des branches parallèles. La façon dont les résistances sont couplées détermine comment elles contribuent à la résistance totale du circuit.
Pas
Méthode 1 sur 4: Connexion en série

1. Apprendre à reconnaître un circuit série. Un circuit série est une boucle unique, sans dérivation. Toutes les résistances ou autres composants sont disposés en séquence.

2. Additionner toutes les résistances. Dans un circuit en série, la résistance totale est égale à la somme de toutes les résistances. Le même courant traverse chaque résistance, de sorte que chaque résistance se comporte comme prévu.

3. Commencez par l`ampérage et la tension à la place. Si vous ne connaissez pas les valeurs de résistance individuelles, vous pouvez les calculer à l`aide de la loi d`Ohm : V = IR ou tension = courant x résistance. La première étape consiste à déterminer le courant dans le circuit et la tension totale :

4. Utiliser ces valeurs dans la loi d`Ohm. Réorganiser V = IR pour résoudre la résistance : R = V / I (résistance = tension / courant). Appliquer les valeurs trouvées à cette formule, pour obtenir la résistance totale.
Méthode 2 sur 4: Circuit parallèle

1. Comprendre ce que sont les circuits parallèles. Un circuit parallèle se divise en plusieurs chemins, qui convergent ensuite à nouveau. Le courant circule dans chaque branche du circuit.
- Si le circuit a des résistances sur la branche principale (avant ou après la branche) ou s`il y a deux résistances ou plus sur une branche, passez aux instructions pour un circuit combiné.

2. Calculer la résistance totale de la résistance dans chaque branche. Étant donné que chaque résistance ne ralentit que le courant traversant une branche, elle n`a qu`un faible effet sur la résistance totale du circuit. La formule de la résistance totale Rt est  , où R1 la résistance est de la première branche, R2 la résistance de la deuxième branche, et ainsi de suite, jusqu`à la dernière branche Rm.
, où R1 la résistance est de la première branche, R2 la résistance de la deuxième branche, et ainsi de suite, jusqu`à la dernière branche Rm.
 , où R1 la résistance est de la première branche, R2 la résistance de la deuxième branche, et ainsi de suite, jusqu`à la dernière branche Rm.
, où R1 la résistance est de la première branche, R2 la résistance de la deuxième branche, et ainsi de suite, jusqu`à la dernière branche Rm.Utilisez la formule
 et résoudre pour Rt:
et résoudre pour Rt:Convertir des fractions au dénominateur commun :


Multiplier les deux côtés par Rt: 1 = 1.6Rt
Rt = 1 / 1.6 = 0.625 ??.

3. Commencez par le courant total et la tension à la place. Si vous ne connaissez pas la valeur des résistances individuelles, vous avez besoin de la valeur du courant et de la tension :

4. Utiliser ces valeurs dans la loi d`Ohm. Si vous connaissez le courant total et la tension sur l`ensemble du circuit, vous pouvez trouver la résistance totale en utilisant la loi d`Ohm : R = V / I.

5. Attention aux branches avec une résistance nulle. Si une branche d`un circuit parallèle n`a pas de résistance, alors tout le courant passe par cette branche. La résistance du circuit est alors de zéro ohm.
Méthode 3 sur 4: Circuit combiné

1. Divisez votre circuit en circuits série et circuits parallèles. Un circuit combiné a un certain nombre de composants connectés en série (l`un après l`autre) et d`autres composants connectés en parallèle (dans différentes branches). Recherchez des parties de votre schéma qui peuvent être simplifiées en un circuit série ou parallèle. Encerclez chacune de ces pièces pour vous aider à vous en souvenir.
- Par exemple, un circuit a une résistance de 1 et une résistance de 1,5 connectées en série. Après la deuxième résistance, le circuit se divise en deux branches parallèles, l`une avec une résistance de 5 et l`autre avec une résistance de 3 Ω.
Entourez les deux branches parallèles pour les distinguer du reste du circuit.

2. Trouver la résistance de chaque section parallèle. Utiliser la formule de résistance parallèle  pour trouver la résistance totale d`une seule section parallèle du circuit.
pour trouver la résistance totale d`une seule section parallèle du circuit.
 pour trouver la résistance totale d`une seule section parallèle du circuit.
pour trouver la résistance totale d`une seule section parallèle du circuit.

 ??
??
3. Simplifiez votre schéma. Une fois que vous avez trouvé la résistance totale d`une section parallèle, vous pouvez rayer toute cette section dans votre diagramme. Traitez cette section comme un seul fil avec une résistance égale à la valeur que vous avez trouvée.

4. Additionner les résistances en série. Une fois que vous avez remplacé chaque circuit parallèle par une seule résistance, votre schéma doit être une seule boucle : un circuit en série. La résistance totale d`un circuit en série est égale à la somme de toutes les résistances individuelles, il suffit donc de les additionner pour obtenir la réponse.
 ??.
??.
5. Utilisez la loi d`Ohm pour trouver les valeurs inconnues. Si vous ne savez pas quelle est la résistance dans un certain composant de votre circuit, cherchez quand même un moyen de la calculer. Si vous connaissez la tension V et le courant I aux bornes de ce composant, déterminez sa résistance à l`aide de la loi d`Ohm : R = V / I.
Méthode 4 sur 4: Formules avec puissance

1. Apprenez la formule du pouvoir. La puissance est le degré auquel le circuit consomme de l`énergie et le degré auquel il fournit de l`énergie à tout ce qui alimente le circuit (comme une lampe). La puissance totale d`un circuit est égale au produit de la tension totale et du courant total. Soit sous forme d`équation : P = VI.
- N`oubliez pas que lorsque vous résolvez cela pour la résistance totale, vous avez besoin de la puissance totale du circuit. Il ne suffit pas de connaître la puissance passant par un composant.

2. Déterminer la résistance en utilisant la puissance et le courant. Connaissant ces valeurs, vous pouvez combiner les deux formules pour déterminer la résistance :

3. Déterminer la résistance en utilisant la puissance et la tension. Si vous ne connaissez que la puissance et la tension, vous pouvez utiliser la même approche pour déterminer la résistance. N`oubliez pas d`utiliser la pleine tension aux bornes du circuit ou la tension de la batterie alimentant le circuit :
Des astuces
- La puissance est mesurée en watts (W).
- La tension est mesurée en volts (V).
- Le courant est mesuré en ampères (A) ou en milliampères (mA). 1 lun =
A = 0,001 A.
- La puissance P telle qu`utilisée dans ces formules fait référence à la mesure directe de la puissance à un moment précis dans le temps. Si le circuit utilise du courant alternatif (AC), la puissance change continuellement. Les électriciens calculent la puissance moyenne des circuits alternatifs à l`aide de la formule Pmoyenne = VIcosθ, où cosθ est le facteur de puissance du circuit.
Articles sur le sujet "Calcul de la résistance totale dans un circuit"
Оцените, пожалуйста статью
Populaire