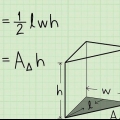
A = 1/2(o)(h) A = 1/2(2)(4) A = 1/2(8) A = 4 cm 

Calculer le volume d'une pyramide
Teneur
Pour calculer le volume d`une pyramide, multipliez l`aire de la base par la hauteur de la pyramide. Divisez le résultat par 3, c`est tout! Lire cet article avec les méthodes de calcul pour une pyramide à base rectangulaire et une pyramide à base triangulaire.
Pas
Méthode 1 sur 2: Pyramide à base rectangulaire

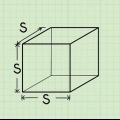
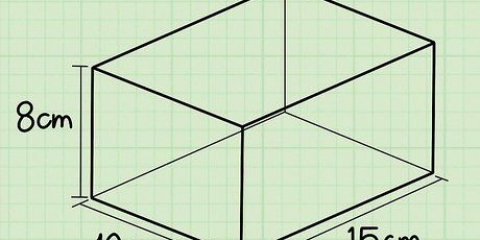
1. Déterminer la longueur et la largeur de la base. Dans cet exemple, la longueur est de 4 cm et la largeur est de 3 cm. Si vous avez une base carrée, la méthode est la même, seules la longueur et la largeur sont égales. Notez vos mesures.

2. Multipliez la longueur par la largeur pour calculer l`aire de la base. Pour calculer l`aire de notre exemple, on multiplie 3 cm par 4 cm. 3cm x 4cm = 12cm

3. Multiplier la surface de la base par la hauteur. La surface de la base est de 12 cm et la hauteur est de 4 cm, donc on multiplie 12 cm par 4 cm. 12cm x 4cm = 48cm

4. Divisez le résultat par 3. C`est la même chose que de multiplier par 1/3. 48cm/3 = 16cm. Le volume d`une pyramide d`une hauteur de 4 cm et d`une base rectangulaire d`une largeur de 3 cm et d`une longueur de 4 cm est donc de 16 cm. N`oubliez pas d`indiquer le résultat en unités cubes.
Méthode 2 sur 2: Pyramide à base triangulaire

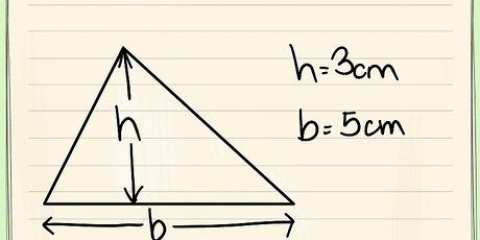
1. Déterminer la longueur et la largeur de la base. La longueur et la largeur de la base devoir perpendiculaires les uns aux autres, sinon cette méthode ne fonctionnera pas. Ils peuvent également être vus comme le bas et la hauteur du triangle. Dans cet exemple, la largeur du triangle est de 2 cm et la longueur est de 4 cm. Notez ceci.

2. Calculer l`aire de la base. Pour calculer l`aire de la base, nous utilisons la formule suivante:A = 1/2(o)(h). C`est comme ça qu`on le fait:

3. Multiplier l`aire de la base par la hauteur de la pyramide. La surface de la base est de 4 cm et la hauteur est de 5 cm. 4 cm x 5 cm = 20 cm.

4. Divisez le résultat par 3. 20 cm/3 = 6,67 cm. Le volume d`une pyramide d`une hauteur de 5 cm et d`une base triangulaire d`une largeur de 2 cm et d`une longueur de 4 cm est donc de 6,67 cm.
Des astuces
- Dans une pyramide à base carrée, la hauteur, la ligne divisant le côté triangulaire en deux triangles égaux et la largeur de la base sont reliées par le théorème de Pythagore : (largeur ÷ 2) + (hauteur) = (hauteur du triangle)
- Cette méthode peut également être appliquée à des objets tels que des pyramides pentagonales, des pyramides hexagonales, etc. Le processus général est le suivant : A) calculer l`aire de la base ; B) mesurer la hauteur du sommet de la pyramide au centre de la base ; C) multiplier A par B; D) diviser par 3.
- Dans tout ordinaire les pyramides sont les côtes droites, la ligne divisant le côté triangulaire en deux triangles égaux et la largeur de la base reliées par le théorème de Pythagore : (longueur du côté ÷ 2) + (longueur de la côte) = (hauteur)
Mises en garde
- Les pyramides ont trois types de hauteurs : la ligne divisant la face triangulaire en deux triangles égaux, la longueur de la nervure (le long du côté d`une face triangulaire) et la hauteur réelle (depuis la pointe de la pyramide perpendiculairement à la base) . ).
Articles sur le sujet "Calculer le volume d'une pyramide"
Оцените, пожалуйста статью
Populaire