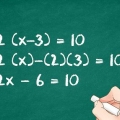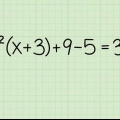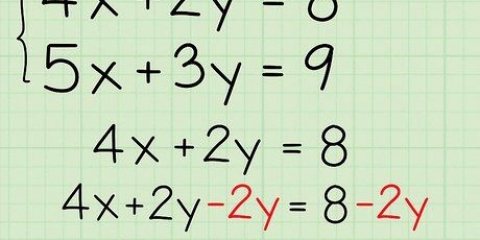Par exemple, 

Par exemple, pour  dans
dans  pour isoler, vous tirez
pour isoler, vous tirez  des deux côtés de l`équation l`équation :
des deux côtés de l`équation l`équation :




Par exemple, pour  à résoudre dans
à résoudre dans  , diviser chaque côté de l`équation par
, diviser chaque côté de l`équation par  :
:



Donc la solution de est est
est  .
. 

Par exemple, réécrivez  donc si
donc si  .
. 
Par exemple,  .
. 
Par exemple, pour le polynôme quadratique  , vous devez trouver deux nombres (
, vous devez trouver deux nombres ( et
et  ), vrai
), vrai  et
et  .
. Parce que tu  vous savez que l`un des nombres sera négatif.
vous savez que l`un des nombres sera négatif. Tu devrais voir ça  et
et  . Alors tu divises
. Alors tu divises  dans
dans  et réécrivez le polynôme quadratique :
et réécrivez le polynôme quadratique :  .
. 
Par exemple, les deux premiers termes du polynôme  sont
sont  . Un terme qui apparaît dans les deux est
. Un terme qui apparaît dans les deux est  . Cela devient le groupe dissous
. Cela devient le groupe dissous  .
. 
Par exemple, les deux seconds termes du polynôme  sont
sont  . Un terme qui apparaît dans les deux est
. Un terme qui apparaît dans les deux est  . Ainsi est le groupe dissous
. Ainsi est le groupe dissous  .
. 
Par exemple, après factorisation par regroupement, . devient  égal à
égal à  .
. Le premier binôme est  .
. Le deuxième binôme est  .
. Donc le polynôme quadratique original,  peut être écrit comme l`expression factorisée
peut être écrit comme l`expression factorisée  .
. 
Par exemple, pour trouver la première solution de  , définir la première expression binomiale égale à
, définir la première expression binomiale égale à  et te perdre
et te perdre  au. Ainsi:
au. Ainsi:



Ainsi, la première solution du polynôme quadratique est
est  .
. 
Par exemple, pour trouver la deuxième solution pour  , définir la deuxième expression binomiale égale à
, définir la deuxième expression binomiale égale à  et te perdre
et te perdre  au. Ainsi:
au. Ainsi:



La deuxième solution du polynôme quadratique est donc égal à
égal à  .
.
Résoudre des polynômes
Teneur
Un polynôme est une expression composée d`addition et de soustraction de termes. Un terme peut être constitué de variables, de constantes et de coefficients. Lorsque vous résolvez des polynômes, vous essayez généralement de savoir pour quels points x = 0. Les polynômes de degré le plus bas ont une ou deux solutions, selon qu`il s`agisse de polynômes linéaires ou de polynômes quadratiques. Ces types de polynômes peuvent être facilement résolus en utilisant l`algèbre élémentaire et la factorisation. Pour résoudre des polynômes de degré supérieur, vous pouvez lire des articles sur wikiHow.
Pas
Méthode 1 sur 2: Résolution d`un polynôme linéaire

1. Déterminez si vous avez affaire à un polynôme linéaire. Un polynôme linéaire est un polynôme du premier degré. Cela signifie qu`aucune variable n`aura un exposant (ou un exposant supérieur à 1). Comme il s`agit d`un polynôme du premier degré, il a exactement une solution.
- Par exemple,
est un polynôme linéaire (ou polynôme), car la variable
n`a pas d`exposant (ce qui est le même qu`un exposant de 1).

2. Rendre l`équation égale à zéro. C`est une étape nécessaire pour résoudre tous les polynômes.


3. Déplacer le terme variable d`un côté. Pour ce faire, en ajoutant ou en soustrayant la constante des deux côtés de l`équation. Une constante est un terme sans variable.
 dans
dans  pour isoler, vous tirez
pour isoler, vous tirez  des deux côtés de l`équation l`équation :
des deux côtés de l`équation l`équation :



4. Résoudre la variable. Habituellement, vous devez diviser chaque côté de l`équation par la constante. Cela donne la solution du polynôme.
 à résoudre dans
à résoudre dans  , diviser chaque côté de l`équation par
, diviser chaque côté de l`équation par  :
:


Donc la solution de est
 est
est  .
.Méthode 2 sur 2: Résolution d`un polynôme quadratique

1. Déterminez si vous avez affaire à un polynôme quadratique. Un polynôme quadratique est une équation quadratique. Cela signifie qu`aucune variable n`a un exposant supérieur à 2. Comme il s`agit d`un polynôme du second degré, il existe deux solutions.
- Par exemple,
est un polynôme quadratique, car la variable
une
a pour exposant.

2. Assurez-vous que le polynôme est écrit par ordre de degré. Cela signifie que le terme avec exposant  est répertorié en premier suivi du terme du premier degré, puis de la constante.
est répertorié en premier suivi du terme du premier degré, puis de la constante.
 est répertorié en premier suivi du terme du premier degré, puis de la constante.
est répertorié en premier suivi du terme du premier degré, puis de la constante. donc si
donc si  .
.
3. Rendre l`équation égale à zéro. C`est une étape nécessaire pour résoudre tous les polynômes.
 .
.
4. Réécrivez l`expression comme une expression à quatre termes. Pour ce faire, divisez le terme du premier degré (de  terme). Vous cherchez deux nombres dont la somme est égale au coefficient du premier degré, et dont le produit est égal à la constante.
terme). Vous cherchez deux nombres dont la somme est égale au coefficient du premier degré, et dont le produit est égal à la constante.
 terme). Vous cherchez deux nombres dont la somme est égale au coefficient du premier degré, et dont le produit est égal à la constante.
terme). Vous cherchez deux nombres dont la somme est égale au coefficient du premier degré, et dont le produit est égal à la constante. , vous devez trouver deux nombres (
, vous devez trouver deux nombres ( et
et  ), vrai
), vrai  et
et  .
. vous savez que l`un des nombres sera négatif.
vous savez que l`un des nombres sera négatif. et
et  . Alors tu divises
. Alors tu divises  dans
dans  et réécrivez le polynôme quadratique :
et réécrivez le polynôme quadratique :  .
.
5. Facteur par regroupement. Pour ce faire, vous devez factoriser un terme qui correspond aux deux premières conditions du polynôme.
 sont
sont  . Un terme qui apparaît dans les deux est
. Un terme qui apparaît dans les deux est  . Cela devient le groupe dissous
. Cela devient le groupe dissous  .
.
6. Factoriser le deuxième groupe. Vous faites cela en factorisant un terme qui apparaît dans les deux seconds termes du polynôme.
 sont
sont  . Un terme qui apparaît dans les deux est
. Un terme qui apparaît dans les deux est  . Ainsi est le groupe dissous
. Ainsi est le groupe dissous  .
.
sept. Réécrire le polynôme en deux binômes. Un binôme est une expression à deux termes. Vous avez déjà un binôme, l`expression entre parenthèses pour chaque groupe. Cette expression doit être la même pour chaque groupe. Le deuxième binôme est fait en combinant les deux termes factorisés de chaque groupe.
 égal à
égal à  .
. .
. .
. peut être écrit comme l`expression factorisée
peut être écrit comme l`expression factorisée  .
.
8. Trouvez la solution d`abord. Vous le faites en résolvant  dans le premier binôme.
dans le premier binôme.
 dans le premier binôme.
dans le premier binôme. , définir la première expression binomiale égale à
, définir la première expression binomiale égale à  et te perdre
et te perdre  au. Ainsi:
au. Ainsi:


Ainsi, la première solution du polynôme quadratique
 est
est  .
.
9. Déterminer la deuxième solution. Tu fais ça en  résoudre dans le deuxième binôme.
résoudre dans le deuxième binôme.
 résoudre dans le deuxième binôme.
résoudre dans le deuxième binôme. , définir la deuxième expression binomiale égale à
, définir la deuxième expression binomiale égale à  et te perdre
et te perdre  au. Ainsi:
au. Ainsi:


La deuxième solution du polynôme quadratique est donc
 égal à
égal à  .
.Des astuces
- Ne vous inquiétez pas des variables, comme t, ou si vous avez une équation qui équivaut à f(x) au lieu de 0. Si la question veut voir des racines, des zéros ou des facteurs, traitez-la comme n`importe quel autre problème.
- Rappelez-vous l`ordre des opérations pendant que vous travaillez - en effaçant d`abord les parenthèses, puis en faisant la multiplication et la division, et enfin l`addition et la soustraction.
Articles sur le sujet "Résoudre des polynômes"
Оцените, пожалуйста статью
Populaire