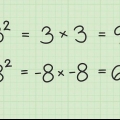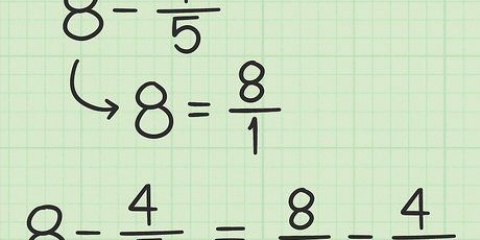30√2 - 4√2 + 10√3 = (30 - 4)√2 + 10√3 = 26√2 + 10√3 

Simplifier 6√(40). Vous pouvez d`abord dissoudre « 40 » dans « 4 x 10 », et vous obtenez 6√(40) = 6√(4×10). Ensuite, vous calculez `2` à partir du carré `4`, et vous multipliez cela par le coefficient actuel. Maintenant vous avez 6√(4×10) = (6x2)√10. Multipliez les deux coefficients et vous obtenez 12√10`.` La tâche se lit désormais comme suit : 12√10 - 3√(10) + √5. Puisque les deux premiers termes ont la même racine, vous pouvez soustraire le deuxième terme du premier et laisser le troisième tel quel. tu aimes maintenant (12-3)√10 + √5 environ, ce qui peut être simplifié en 9√10 + √5. 

Parce que 9 équivaut à (3x3), peux-tu simplifier ceci : 9 devient 3. Parce que 4 équivaut à (2x2), peux-tu simplifier ceci : √4 devient 2. Maintenant la somme 3 + 2 = 5. Parce que 5 et 3√2 ne sont pas des termes égaux, il n`y a plus rien à faire maintenant. Votre réponse finale est 5 - 3√2. 
Assurez-vous que ces termes ont le même dénominateur. Le plus petit dénominateur commun ou dénominateur divisible par « 4 » et « 2 » est « 4 ». Donc, pour faire le deuxième terme ((√2)/2) avec un dénominateur 4, vous devez multiplier à la fois le numérateur et le dénominateur par 2/2. (√2)/2 x 2/2 = (2√2)/4. Additionner le dénominateur des fractions ensemble tout en gardant le même dénominateur. Faites ce que vous feriez si vous ajoutiez des fractions. (√2)/4 + (2√2)/4 = 3√2)/4`.`
Additionner et soustraire des racines carrées
Teneur
Pour ajouter et soustraire des racines carrées, vous devez combiner des racines carrées avec la même racine. Cela signifie que vous pouvez ajouter (ou soustraire de) 2√3 à 4√3, mais vous ne pouvez pas ajouter 2√3 et 2√5. Il existe de nombreux cas où vous pouvez simplifier le nombre sous le radical pour pouvoir combiner des termes similaires et ajouter et soustraire des racines carrées librement.
Pas
Partie 1 sur 2: Maîtriser les bases

1. Simplifier les termes sous les radicaux si possible. Pour simplifier les termes sous les radicaux, essayez de les factoriser dans au moins un carré parfait, tel que 25 (5 x 5) ou 9 (3 x 3). Une fois que vous avez fait cela, vous pouvez prendre la racine carrée du carré parfait et le placer en dehors des radicaux, en laissant le facteur restant en dessous du radical. Dans cet exemple, nous partons du problème 6√50 - 2√8 + 5√12. Les nombres en dehors du radical sont les coefficients et les nombres en dessous, nous appelons le nombres racine. Voici comment simplifier les termes :
- 6√50 = 6√ (25 x 2) = (6 x 5)√2 = 30√2. Vous avez dissous « 50 » dans « 25 x 2 », puis placé « 5 » en dehors de la racine (la racine de « 25 »), après quoi « 2 » reste en dessous du radical. Ensuite, vous multipliez « 5 » par « 6 », le nombre qui était déjà en dehors du radical, et vous obtenez 30 comme nouveau coefficient.
- 2√8 = 2√(4x2) = (2x2)√2 = 4√2. Ici, vous avez pris en compte « 8 » dans « 4 x 2 », puis soustrait la racine carrée de 4 de sorte qu`il vous reste « 2 » en dehors du radical et un « 2 » en dessous du radical. Ensuite, vous multipliez « 2 » par « 2 », le nombre qui était déjà en dehors du radical, et vous obtenez 4 comme nouveau coefficient.
- 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Ici, vous avez pris en compte « 12 » dans « 4 x 3 », puis soustrait la racine carrée de 4 de sorte qu`il vous reste « 2 » en dehors du radical et un « 3 » en dessous du radical. Ensuite, vous multipliez « 2 » par « 5 », le nombre qui était déjà en dehors du radical, et vous obtenez 10 comme nouveau coefficient.

2. Encerclez tous les termes avec les numéros de racine correspondants. Une fois que vous avez simplifié les nombres racines des termes donnés, vous vous retrouvez avec l`équation suivante : 30√2 - 4√2 + 10√3. Étant donné que vous ne pouvez ajouter ou soustraire que des racines similaires, vous devez encercler ces termes avec la même racine, dans cet exemple : 30√2 et 4√2. Vous pouvez comparer cela à l`addition ou à la soustraction de fractions, où vous ne pouvez ajouter ou soustraire les termes que si les dénominateurs sont égaux.

3. Si vous travaillez avec une équation plus longue et qu`il existe plusieurs paires de nombres racines correspondants, vous pouvez encercler la première paire, souligner la seconde, astérisque la troisième, etc. Mettre des termes similaires dans l`ordre vous permettra de visualiser plus facilement la solution.

4. Calculer la somme des coefficients des termes de racines égales. Il ne vous reste plus qu`à calculer la somme des coefficients des termes de racines égales, en ignorant les autres termes de l`équation. Les nombres racines restent inchangés. L`idée est que vous indiquez combien de ce type de nombre racine il y a, au total. Les termes discordants peuvent rester tels quels. Voici ce que vous faites :
Partie 2 sur 2: Plus d`exercice

1. Faire l`exemple 1. Dans cet exemple, vous ajoutez les racines carrées suivantes : (45) + 4√5. Vous devez effectuer les opérations suivantes :
- Simplifier (45). Vous pouvez d`abord le délier comme ceci (9 x 5).
- Ensuite, vous prenez la racine carrée de neuf et vous obtenez « 3 », que vous placez ensuite en dehors de la racine carrée. Alors, (45) = 3√5.
- Ajoutez maintenant les coefficients des deux termes avec des racines correspondantes pour obtenir votre réponse. 3√5 + 4√5 = 7√5

2. Faire l`exemple 2. L`exemple suivant est cette affectation : 6√(40) - 3√(10) + √5. Vous devez procéder comme suit pour résoudre ce problème :
3. Faire l`exemple 3. Cet exemple va comme ceci : 9√5 -2√3 - 4√5. Aucune des racines ne contient de carré, donc aucune simplification n`est possible. Les premier et troisième termes ont des racines égales, donc leurs coefficients peuvent être soustraits (9 - 4). Le numéro de racine reste le même. Les termes restants ne sont pas égaux, le problème peut donc être simplifié en5√5 - 2√3`.`


4. Faire l`exemple 4. Supposons que vous ayez affaire au problème suivant : 9 + √4 - 3√2 Vous devez maintenant effectuer les opérations suivantes :

5. Faire l`exemple 5. Essayons de faire la somme des racines carrées qui font partie d`une fraction. Tout comme une fraction ordinaire, vous ne pouvez désormais calculer que la somme des fractions ayant le même numérateur ou dénominateur. Disons que vous travaillez avec ce problème : (√2)/4 + (√2)/2, Maintenant, procédez comme suit :
Des astuces
- Les nombres racines avec un carré comme facteur doivent toujours être simplifiés pour vous allez déterminer et combiner des nombres racines égaux.
Mises en garde
- Vous ne pouvez jamais combiner des nombres racines inégaux.
- Vous ne pouvez jamais combiner un entier et une racine carrée. Alors: 3 + (2x) pouvez ne pas être simplifié.
- Remarque : `(2x) est le même que `(√(2x)`.
Articles sur le sujet "Additionner et soustraire des racines carrées"
Оцените, пожалуйста статью
Similaire
Populaire