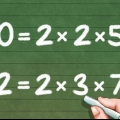Ajouter les nombres de 1 à N : 7 étapes (avec photos)

Teneur

Pas
- Méthode 1 sur 1 : deuxième partie : utiliser la somme de 1 à N pour trouver la somme de deux nombres entiers
Des astuces
Mises en garde

Les entiers sont des entiers sans fractions ni décimales. Si un problème mathématique vous oblige à additionner un nombre d`entiers de 1 à une valeur donnée N, alors il n`est pas nécessaire d`ajouter chaque valeur à la main. Au lieu de cela, pour gagner du temps et des efforts, utilisez l`équation (N(N + 1)) / 2, où N représente le nombre le plus élevé de la série.

Pas

Image intitulée Sum the Integers from 1 to N Step 1

1. Définir le plus grand entier comme N. Lors de l`ajout d`entiers de 1 à un nombre donné N, vous devez définir N lui-même comme un entier positif. N est un nombre entier et ne peut donc pas être un nombre décimal ou fractionnaire. N ne doit pas non plus être négatif.

Par exemple, disons que nous voulons ajouter tous les entiers de 1 à 100. Dans ce cas, 100 est la valeur de N, car c`est le dernier nombre de notre série, ou, en d`autres termes, le plus grand nombre de l`addition.

Image intitulée Sum the Integers from 1 to N Step 2

2. Multiplier N(N + 1) et diviser par 2. Une fois que vous avez défini la valeur de N, appliquez cette valeur à l`équation (N(N + 1))/2. Cette équation trouve la somme de tous les nombres entiers compris entre 1 et N.

Dans notre exemple, nous allons remplir 100, la valeur de N, dans l`équation. (N(N + 1))/2 devient alors (100 (100 + 1))/2.

Image intitulée Sum the Integers from 1 to N Step 3

3. Calculer la réponse. La valeur finale de cette équation est la somme de tous les nombres entre 1 et N.

Résolvons cet exemple.

(100(100 + 1))/2 =

(100(101))/2 =

(10100)/2 =

5050. la somme de tous les nombres entiers de 1 à 100 est 5050.

Image intitulée Sum the Integers from 1 to N Step 4

4. Comprendre comment l`équation (N(N + 1))/2 est dérivée. Revoyez l`exemple de problème. Divisez cette séquence 1 + 2 + 3 + 4... + 99 + 100 en deux groupes -- de 1 à 50 et un de 51 à 100. Si vous ajoutez le premier nombre du premier groupe (1) au dernier nombre du deuxième groupe (100), vous obtenez 101. Vous obtenez la même réponse (101) à 2 + 99, 3 + 98, 4 + 97, et ainsi de suite. Si nous ajoutons chaque nombre du premier groupe à son nombre correspondant dans le deuxième groupe, nous obtenons 50 paires de nombres avec la même somme : 101. Donc, 50 x 101 = 5050, la somme des nombres entiers de 1 à 100. Notez que 50 est la moitié de 100, et que 101 est 100 + 1. En fait, cette observation s`applique à la somme de tout nombre entier positif - la somme des composants peut être divisée en deux groupes, et les nombres de ces groupes peuvent être attribués les uns aux autres de telle manière que chaque paire a la même somme. Notez qu`une séquence impaire d`entiers laisse un nombre -- cela n`affecte pas la réponse finale.

En général on peut dire que pour tout nombre N, la somme des nombres de 1 à N est égale à (N/2)(N + 1). La forme simplifiée de cette équation est (N(N + 1))/2, l`équation de la somme des nombres entiers.

Méthode 1 sur 1 : deuxième partie : utiliser la somme de 1 à N pour trouver la somme de deux nombres entiers

Image intitulée Sum the Integers from 1 to N Step 5

1. Décidez s`il faut ajouter inclusif ou exclusif. Souvent, le but n`est pas de sommer une plage d`entiers de 1 à un nombre donné, mais il vous sera demandé de trouver la somme d`une série d`entiers compris entre deux nombres entiers N₁ et n₂, où N₁ > N₂ et les deux > être 1. Le processus pour trouver cette somme est relativement simple, mais avant de commencer, nous devons décider si la somme est inclusive ou exclusive - en d`autres termes, si le N₁ et n₂ comprend ou seul les nombres entiers entre les deux, car la procédure est légèrement différente dans ces cas.

Image intitulée Sum the Integers from 1 to N Step 6

2. Pour déterminer la somme des nombres entiers entre deux nombres N₁ et n₂ nous déterminons d`abord la somme de chaque valeur de N séparément et la soustrayons. En général, il vous suffit de soustraire la somme de la plus petite valeur N de la somme de la plus grande valeur N pour trouver la réponse. pourtant, comme mentionné ci-dessus, il est important de savoir si cet ajout est inclusif ou exclusif. L`addition inclusive vous oblige à soustraire 1 de la valeur de N₂ avant de le mettre dans l`équation, tandis que l`énumération exclusive vous oblige à soustraire 1 de la valeur de N₁.

Disons qu`on a demandé le compris somme pour déterminer les nombres entiers entre N₁ = 100 et N₂ = 75. En d`autres termes, nous devons trouver la somme de la séquence 75 + 76 + 77 ... + 99 + 100. Pour ce faire, on prend la somme des entiers de 1 à N₁, et soustraire cette somme des nombres entiers de 1 à N₂ - 1 (rappelez-vous que nous ajoutons inclusif, donc nous soustrayons 1 de N₂), et procédez comme ceci :

(N₁(N₁ + 1))/2 - ((N₂-1)((N₂-1) + 1))/2 =

(100(100 + 1))/2 - (74(74 + 1))/2 =

5050 - (74(75))/2 =

5050 - 5550/2 =

5050 – 2775 = 2275. La somme inclusive des nombres entiers compris entre 75 et 100 est 2275.

allons maintenant exclusif commencer à compter. L`équation reste la même, sauf dans ce cas on soustrait 1 de N₁ au lieu de N₂:

((N₁-1)((N₁-1) + 1))/2 - (N₂(N₂ + 1))/2 =

(99(99 +1))/2 - (75(75 + 1))/2 =

(99(100))/2 - (75(76))/2 =

9900/2 – 5700/2 =

4950 – 2850 = 2100. La somme exclusive des nombres entiers compris entre 75 et 100 est 2100.

Image intitulée Sum the Integers from 1 to N Step 7

3. Comprendre pourquoi ce processus fonctionne. Considérons la somme des nombres entiers de 1 à 100 comme 1 + 2 + 3... + 98 + 99 + 100 et la somme des nombres entiers de 1 à 75 comme 1 + 2 + 3 ... + 73 + 74 + 75. La somme inclusive des nombres entiers de 75 à 100 signifie 75 + 76 + 77 ... + 99 + 100. La somme de 1-75 et 1-100 est la même jusqu`à ce qu`un avec 75 --– à ce stade, la somme de 1-75 "s`arrête" et la somme de 1 - 100 continue, avec ... 75 + 76 + 77 ... + 99 + 100. Par conséquent, soustraire la somme des entiers de 1-75 de la somme des entiers de 1-100 nous permet de séparer la somme des entiers de 75-100.

Cependant, si nous additionnons inclusivement, nous devons utiliser la somme de 1-74 au lieu de la somme de 1-75 pour s`assurer que 75 est inclus dans la somme finale.

De même, en plus exclusif, nous utilisons la somme de 1-99, plutôt que la somme de 1-100, pour s`assurer que 100 n`est pas inclus dans la somme. Nous pouvons utiliser la somme de 1-75, car soustraire cette somme de la somme de 1-99 exclut le nombre 75 de notre somme finale.

Des astuces

Le résultat est toujours un nombre entier, car n ou n+1 est pair et peut donc être divisé par 2.
En bref : SOMME(1 à n) = n(n+1)/2
SOMME(a à b)= SOMME(1 à b) - SOMME(1 à a-1).

Mises en garde

Bien que les généralisations aux nombres négatifs ne soient pas très difficiles, cette explication est limitée à tous les entiers positifs N, où N est au moins 1.