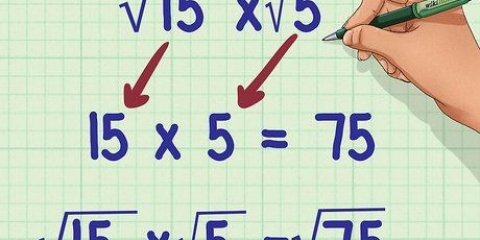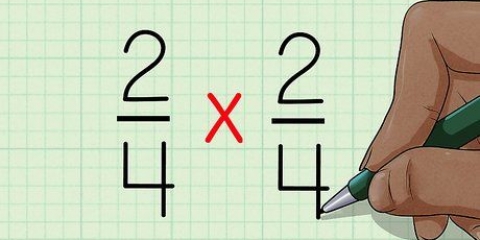Multiplication de nombres racines

Teneur

Pas
Des astuces

Le symbole racine (√) représente la racine carrée d`un nombre. Vous pouvez rencontrer le symbole de la racine en mathématiques, ou même en menuiserie ou dans tout autre domaine où la géométrie entre en jeu ou lors du calcul de dimensions ou de distances relatives. Vous pouvez multiplier les racines qui ont le même pouvoir (racines du pouvoir). Si les radicaux n`ont pas le même pouvoir, vous pouvez modifier leur équation jusqu`à ce qu`ils le fassent. Si vous voulez savoir comment multiplier des racines avec ou sans coefficients, suivez les étapes ci-dessous.

Pas

Méthode 1 sur 3: Multiplication de racines sans coefficients

Image intitulée Multiply Radicals Step 1

1. Assurez-vous que les racines ont le même pouvoir. Afin de multiplier les racines en utilisant la méthode de base, elles doivent avoir la même puissance. Le « pouvoir » est le petit nombre écrit à gauche de la ligne supérieure du symbole de la racine. Si aucune puissance n`est spécifiée, alors vous avez affaire à une racine carrée (seconde puissance) et elle peut être multipliée par d`autres racines carrées. Vous pouvez multiplier les racines de différentes puissances ensemble, mais c`est une méthode avancée et sera expliquée plus tard. Voici deux exemples de racines multiplicatrices avec les mêmes pouvoirs :

Ex. 1: (18) x √(2) = ?
Ex. 2: (10) x (5) = ?
Ex. 3: (3) x √(9) = ?

Image intitulée Multiply Radicals Step 2

2. Multiplier les nombres sous le radical. Ensuite, vous multipliez les nombres sous le signe radical et le laissez là. Cela se passe comme ceci :

Ex. 1: (18) x (2) = √(36)

Ex. 2: (10) x (5) = (50)

Ex. 3: (3) x √(9) = (27)

Image intitulée Multiply Radicals Step 3

3. Simplifier les racines. Une fois que vous avez multiplié les racines, il y a de fortes chances qu`elles puissent être simplifiées en un carré parfait ou une puissance de deux, ou elles peuvent être simplifiées en trouvant un carré comme facteur du produit final. Vous procédez comme suit :

Ex. 1 : (36) = 6. 36 est un carré car c`est un produit de 6 x 6. La racine carrée de 36 est juste 6.

Ex. 2: (50) = (25 x 2) = ([5 x 5] x 2) = 5√(2). Bien que 50 ne soit pas un nombre carré, 25 est un facteur de 50 (car il correspond exactement à deux fois) et est un carré parfait. Vous pouvez factoriser 25 (5 x 5) et placer un 5 à l`extérieur du radical pour simplifier l`équation.

Vous pouvez y penser comme ceci : si vous remettez le 5 sous le signe radical, il se multipliera de lui-même et redeviendra 25.

Ex. 3:√(27) = 3. 27 a est un cube parfait (troisième puissance), car c`est le produit de 3 x 3 x 3. La racine carrée de 27 est donc 3.

Méthode 2 sur 3: Multiplication des racines par des coefficients

Image intitulée Multiply Radicals Step 4

1. Multiplier les coefficients. Les coefficients sont les nombres en dehors du radical. Si aucun coefficient n`est donné, vous pouvez considérer le coefficient comme 1. Multiplier les coefficients entre eux. Vous procédez comme suit :

Ex. 1: 3√(2) x √(10) = 3√( ? )

3 x 1 = 3

Ex. 2: 4√(3) x 3√(6) = 12√( ? )

4x3 = 12

Image intitulée Multiply Radicals Step 5

2. Multiplier les nombres dans les racines. Après avoir multiplié les coefficients, vous pouvez commencer à multiplier les nombres à l`intérieur des racines. Vous procédez comme suit :

Ex. 1: 3√(2) x √(10) = 3√(2 x 10) = 3√(20)

Ex. 2: 4√(3) x 3√(6) = 12√(3 x 6) = 12√(18)

Image intitulée Multiply Radicals Step 6

3. Simplifier le produit. Ensuite, vous simplifiez les nombres sous les racines en cherchant les carrés parfaits ou les multiples des nombres sous les racines qui composent les carrés parfaits. Une fois que vous avez simplifié ces termes, multipliez leurs coefficients correspondants par. Vous procédez comme suit :

3√(20) = 3√(4 x 5) = 3√([2 x 2] x 5) = (3 x 2)√(5) = 6√(5)

12√(18) = 12√(9 x 2) = 12√(3 x 3 x 2) = (12 x 3)√(2) = 36√(2)

Méthode 3 sur 3: Multiplier différentes racines de pouvoir

Image intitulée Multiply Radicals Step 7

1. Trouver le LCF (Least Common Multiple) des puissances. Pour trouver le LCF des puissances, trouvez le plus petit nombre divisible par les deux puissances. Trouvez le LCF des indices pour l`équation suivante : √(5) x √(2) = ?

Les indices sont 3 et 2. 6 est le LCF de ces deux nombres, car c`est le plus petit nombre divisible par 3 et 2. 6/3 = 2 et 6/2 = 3. Pour multiplier les racines, les deux puissances doivent être 6.

Image intitulée Multiply Radicals Step 8

2. Écrivez chaque expression avec le nouveau LCF comme puissance. Les expressions ressembleront à ceci par rapport à leurs nouveaux pouvoirs :

(5) x √(2) = ?

Image intitulée Multiply Radicals Step 9

3. Trouvez le nombre par lequel vous devez multiplier chacune des puissances d`origine pour déterminer le LCF. Avec l`expression (5) votre puissance de 3 devra être multipliée par 2 pour obtenir 6. Avec l`expression (2) vous devrez multiplier la puissance 2 par 3 pour obtenir 6.

Image intitulée Multiply Radicals Step 10

4. Faire de ce nombre l`exposant du nombre dans la racine carrée. Dans la première équation, 2 devient la puissance 5. Dans la deuxième équation, 3 devient la puissance de 2. Cela ressemblera à ceci :

--> (5) = (5)

--> (2) = (2)

Image intitulée Multiply Radicals Step 11

5. Multiplier les nombres dans les racines par leurs exposants. Vous procédez comme suit :

(5) = (5 x 5) = √25

(2) = √(2 x 2 x 2) = √8

Image intitulée Multiply Radicals Step 12

6. Placez ces nombres sous un radical. Placez-les sous un signe radical et reliez-les avec un signe de multiplication. Voici à quoi ressemble le résultat : (8 x 25)

Image intitulée Multiply Radicals Step 13

sept. Multiplier. (8 x 25) = (200). C`est la réponse finale. Dans certains cas, vous pourrez peut-être simplifier encore plus ces expressions - par exemple, si vous pouvez trouver un nombre qui, multiplié six fois par lui-même, produit 200. Mais ce n`est pas possible, ce qui signifie que l`expression ne peut pas être simplifiée davantage.

Des astuces

S`il y a un signe plus ou moins entre un nombre et le radical, alors ce n`est pas un coefficient - auquel cas c`est un terme distinct et doit être traité séparément du radical. Si un radical et un autre terme sont entre parenthèses -- par exemple, (2 + 5), alors vous devez traiter à la fois 2 et 5 séparément lorsque vous effectuez des opérations à l`intérieur des parenthèses, mais lorsque vous effectuez des opérations en dehors des parenthèses, vous devez considérer (2 + √5) comme un tout.
Les signes de racine sont une autre façon d`exprimer les exposants fractionnaires. En d`autres termes, la racine carrée d`un nombre est la même que ce nombre élevé à la puissance 1/2, la racine cubique de tout nombre est la même que ce nombre élevé à la puissance 1/3, et ainsi de suite.
Une "coefficient" est le nombre (s`il y a un nombre) immédiatement avant le radical. Donc dans l`expression 2√5, 5 est en dessous du radical et le nombre 2 (en dehors du radical) est le coefficient. Lorsqu`une racine et un coefficient sont représentés comme un groupe, cela signifie que la racine et le coefficient doivent être multipliés l`un par l`autre, comme dans l`exemple : 2 * √5.