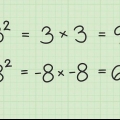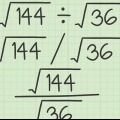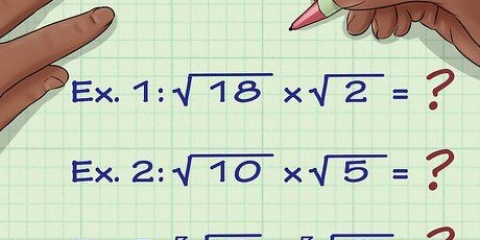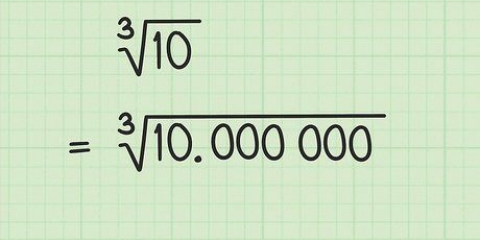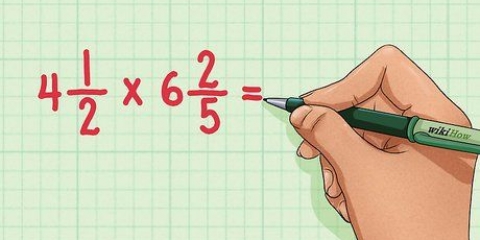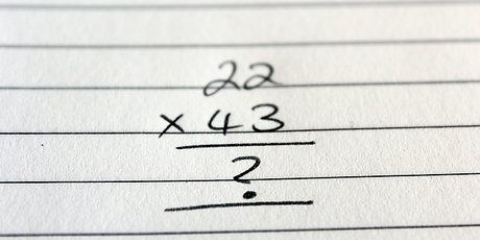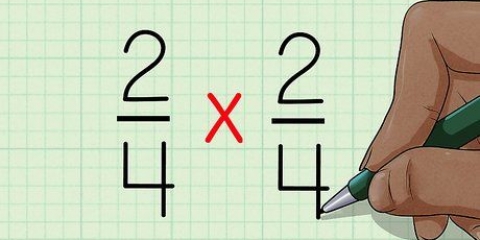Multiplication de racines carrées : 8 étapes (avec des photos)

Teneur

Pas
- Méthode 1 sur 2: Multiplication de racines carrées sans coefficients
- Méthode 2 sur 2: Multiplication de racines carrées avec des coefficients
Des astuces
Nécessités

Tout comme pour multiplier des nombres entiers, vous pouvez également multiplier des racines carrées (une équation de racine carrée) ensemble. Parfois, les racines carrées ont des coefficients (un entier avant le radical), mais cela ajoute juste une étape à la multiplication et ne change pas le processus. La partie la plus délicate de la multiplication de racine carrée est de simplifier l`expression pour obtenir la réponse finale, mais même cette étape est facile si vous connaissez vos carrés parfaits.

Pas

Méthode 1 sur 2: Multiplication de racines carrées sans coefficients

Image intitulée Multiplier les racines carrées Étape 1

1. Multipliez les racines ensemble. Un radicand (anglais) est un nombre en dessous du radical. Multiplier les racines de la même manière que les entiers. Assurez-vous que le produit reste en dessous du signe radical.

Par exemple, si vous calculez $\sqrt{15} \times \sqrt{5}$ ${sqrt{15}}times {sqrt{5}}$ , alors vous obtenez $15 \times 5 = 75$ $15fois 5=75$ . alors, $\sqrt{15} \times \sqrt{5} = \sqrt{75}$ ${sqrt{15}}times {sqrt{5}}={sqrt{75}}$ .

Image intitulée Multiplier les racines carrées Étape 2

2. Déduire tous les carrés parfaits de la racine carrée. Pour ce faire, vérifiez si un carré parfait est un facteur du nombre sous le radical. Si vous ne parvenez pas à dériver un carré parfait, votre réponse a déjà été simplifiée et vous n`avez rien d`autre à faire.

Un carré parfait est le résultat de la multiplication d`un nombre (entier positif ou négatif) par lui-même. Par exemple : 25 est un carré parfait car

5 \times 5 = 25

$5fois 5=25$ .

Par exemple,

\sqrt{75}

${sqrt{75}}$ peut être pris en compte dans le carré parfait 25 :

\sqrt{75}

${sqrt{75}}$
=

\sqrt{25 \times 3}

${sqrt{25fois 3}}$

Image intitulée Multiplier les racines carrées Étape 3

3. Placer la racine carrée avant le radical. Laissez l`autre facteur sous le radical. Vous avez maintenant l`expression simplifiée.

Par exemple,

\sqrt{75}

${sqrt{75}}$ peut être dissous dans

\sqrt{25 \times 3}

${sqrt{25fois 3}}$ , pour la racine carrée de 25 (qui est 5):

\sqrt{75}

${sqrt{75}}$
=

\sqrt{25 \times 3}

${sqrt{25fois 3}}$
=

5 \sqrt{3}

$5{sqrt{3}}$

Image intitulée Multiplier les racines carrées Étape 4

4. Calculer le carré d`une racine carrée. Dans certains cas, vous devez multiplier une racine carrée par elle-même. Mettre un nombre au carré et prendre la racine carrée d`un nombre sont des opérations opposées ; donc ils se défont l`un l`autre. Le résultat du carré d`une racine carrée est simplement le nombre sous le radical.

Par exemple,

\sqrt{25} \times \sqrt{25} = 25

${sqrt{25}}times {sqrt{25}}=25$ . Vous obtenez ce résultat parce que

\sqrt{25} \times \sqrt{25} = 5 \times 5 = 25

${sqrt{25}}times {sqrt{25}}=5times 5=25$ .

Méthode 2 sur 2: Multiplication de racines carrées avec des coefficients

Image intitulée Multiplier les racines carrées Étape 5

1. Multiplier les coefficients. Un coefficient est un nombre pour le radical. Ignorez simplement le radical et le nombre en dessous et multipliez les deux entiers ensemble. Placer leur produit avant le premier radical.

Attention aux signes plus et moins lors de la multiplication des coefficients. N`oubliez pas qu`un nombre négatif multiplié par un nombre positif produit un résultat négatif et qu`un nombre négatif multiplié par un nombre négatif produit un résultat positif.
Par exemple, lors du calcul $3 \sqrt{2} \times 2 \sqrt{6}$ $3{sqrt{2}}times 2{sqrt{6}}$ , calculer d`abord $3 \times 2 = 6$ $3fois 2=6$ . Maintenant, la tâche est la suivante : $6 \sqrt{2} \times \sqrt{6}$ $6{sqrt{2}}times {sqrt{6}}$ .

Image intitulée Multiplier les racines carrées Étape 6

2. Multiplier les nombres sous les radicaux. Pour ce faire, multipliez les nombres comme s`il s`agissait de nombres entiers. Assurez-vous que le produit reste sous le signe radical.

Par exemple, pour une déclaration comme

6 \sqrt{2} \times \sqrt{6}

$6{sqrt{2}}times {sqrt{6}}$ , calculer le produit des nombres sous les radicaux en utilisant

2 \times 6 = 12

$2fois 6=12$ , de sorte que

\sqrt{2} \times \sqrt{6} = \sqrt{12}

${sqrt{2}}times {sqrt{6}}={sqrt{12}}$ . La tâche ressemble maintenant à ceci :

6 \sqrt{12}

$6{sqrt{12}}$ .

Image intitulée Multiplier les racines carrées Étape 7

3. Si possible, factorisez les carrés sous le signe radical. Vous devez le faire pour simplifier votre réponse. Si vous ne pouvez pas résoudre un carré, votre réponse a déjà été simplifiée et vous pouvez sauter cette étape.

Un carré est le résultat de la multiplication d`un nombre entier (positif ou négatif) par lui-même. Par exemple : 4 est un carré, car

2 \times 2 = 4

$2fois 2=4$ .

Par exemple:

\sqrt{12}

${sqrt{12}}$ peut être factorisé pour que le carré de 4 soit placé avant le radical :

\sqrt{12}

${sqrt{12}}$
=

\sqrt{4 \times 3}

${sqrt{4fois 3}}$

Image intitulée Multiply Square Roots Step 8

4. Multiplier la racine du carré par le coefficient. Laissez l`autre facteur sous le radical. Cela donne une expression simplifiée.

Par exemple,

6 \sqrt{12}

$6{sqrt{12}}$ peut être dissous dans

6 \sqrt{4 \times 3}

$6{sqrt{4fois 3}}$ , après quoi vous pouvez prendre la racine carrée de 4 (c`est-à-dire 2) après quoi vous la multipliez par 6 :

6 \sqrt{12}

$6{sqrt{12}}$
=

6 \sqrt{4 \times 3}

$6{sqrt{4fois 3}}$
=

6 \times 2 \sqrt{3}

$6fois 2{sqrt{3}}$
=

12 \sqrt{3}

$12{sqrt{3}}$

Des astuces

Connaissez vos carrés, car cela rend ce processus beaucoup plus facile!
Suivez les règles habituelles du signe d`un nombre pour déterminer si le nouveau coefficient sera positif ou négatif. Un coefficient positif multiplié par un coefficient négatif donne un nombre négatif. Deux coefficients positifs multipliés ensemble ou deux coefficients négatifs multipliés ensemble donnent un nombre positif.
Tous les termes sous le radical sont toujours positifs, vous n`avez donc pas à vous soucier du signe lorsque vous multipliez des nombres sous un radical.