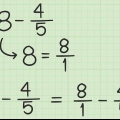Soustraire des nombres

Teneur

Pas
Des astuces
Mises en garde

Les soustractions sont ces sommes où vous soustrayez deux nombres l`un de l`autre. C`est assez simple si vous voulez soustraire des nombres entiers les uns des autres, mais cela devient un peu plus compliqué lorsque vous travaillez avec des fractions ou des nombres décimaux. Une fois que vous avez maîtrisé la soustraction, vous pouvez passer aux concepts mathématiques plus compliqués et ajouter, multiplier et diviser des nombres sera beaucoup plus facile.

Pas

Méthode 1 sur 6: Soustraire de grands nombres entiers en empruntant

1. Notez le plus grand nombre. Supposons que vous travaillez avec la somme 32 - 17. Notez 32 d`abord.

2. Écrivez le plus petit nombre juste en dessous. Assurez-vous que les dizaines et les uns sont bien alignés afin que les 3 pouces "32" directement au-dessus de 1 dans "17" état, et le 2 dans "32" juste au-dessus du "sept" à 17 ans.

3. Soustraire le nombre du bas du haut. Cela peut devenir un peu délicat si le nombre du bas est supérieur à celui du haut. Dans ce cas 7 est supérieur à 2. Voici ce qu`il faut faire :

tu vas devoir "prêter" des 3 dans "32" faire le 2 a 12.

Traverser le 3 de "32" et faites-en un 2, puis faites de l`unité 2 un 12.

Maintenant vous avez 12 – 7 = 5. Écrivez un 5 sous la colonne des unités.

4. Soustraire le dix du nombre du bas du dix du nombre du haut. N`oubliez pas que le 3 sur 32 est devenu un 2. Soustrayez maintenant le 1 sur 17 des 2 au-dessus, donc 2-1 = 1. Écrivez 1 sous la colonne des dizaines. Si tout va bien, vous avez maintenant 15 comme réponse, donc 32 - 17 = 15.

5. Vérifie ton travail. Si vous voulez vous assurer que vous avez fait le calcul correctement, il vous suffit d`ajouter la réponse au plus petit nombre pour récupérer le plus grand nombre. Donc à vérifier : 15 + 17 = 32, donc tu as bien fait. Excellent!

Méthode 2 sur 6: Soustraire de petits nombres entiers

1. Déterminer quel nombre est le plus grand. Un exercice tel que 15 - 9 nécessite une approche différente de 2 - 30.

Dans la somme 15 - 9, le premier nombre, 15, est le plus grand.
Dans la somme 2 - 30, le deuxième nombre, 30 est le plus grand.

2. Décidez si votre réponse doit être positive ou négative. Si le premier nombre est le plus grand, alors la réponse est positive. Si le deuxième nombre est le plus grand, la réponse est négative.

Donc dans la première somme, 15 - 9, la réponse devient positive, car 15 est supérieur à 9.

Donc dans la deuxième somme, 2 - 30, la réponse devient négative, car 2 est inférieur à 30.

3. Trouver la différence entre les deux nombres. Pour soustraire deux nombres, calculez la différence entre eux.

Pour le problème 15 - 9, prenez 15 pièces. Retirez 9 et comptez combien il en reste (6). Donc, 15 - 9 = 6. Ou utilisez une droite numérique et dessinez les chiffres de 1 à 15 le long de la ligne, puis rayez 9 de 15 vers le bas pour arriver à 6.

Avec la somme 2 - 30, il est plus facile de retourner les nombres et de rendre la réponse négative. Donc, 30 - 2 = 28, et avec cela 2 - 30 est -28.

Méthode 3 sur 6: Soustraction de nombres décimaux

1. Écrivez le plus grand nombre au-dessus du plus petit nombre pour que les décimales soient alignées. Supposons que vous ayez le problème suivant : 10,5 - 8,3. Écrivez le 10,5 au-dessus de 8,3 de manière à ce que les virgules soient au-dessus les unes des autres.

Si vous avez un problème où un nombre a plus de décimales que l`autre, remplissez l`espace vide avec des zéros. Par exemple, si vous avez le problème 5.32 - 4.2, vous pouvez le réécrire comme 5.32 = 4.20. Cela ne change pas la valeur d`un nombre, mais vous vous assurez que les deux nombres peuvent être plus facilement soustraits l`un de l`autre.

2. Soustraire les dixièmes les uns des autres. La soustraction de ces nombres est la même qu`avec les entiers, sauf qu`il faut faire attention à la virgule décimale, alignée et incluse dans la réponse. Dans ce cas, vous devez soustraire 3 de 5. 5 - 3 = 2, donc vous écrivez un 2 sous le 3 dans 8.3.

N`oubliez pas d`inclure le point décimal (la virgule) dans la réponse. Il ressemble maintenant à ceci : ,2.

3. Soustrayez maintenant les unités les unes des autres. Maintenant, soustrayez 8 de 0. Emprunter une douzaine de 1 (à côté du 0) pour faire 10, maintenant soustraire 8 de 10. Vous pouvez également calculer immédiatement la somme 10 – 8 = 2, sans l`étape intermédiaire d`emprunt, car le nombre du bas n`a pas de dix. Écrivez la réponse sous 8.

4. Donc la réponse finale sera 2.2.

Méthode 4 sur 6: Soustraction de fractions

1. Mettre les numérateurs et les dénominateurs ensemble. Supposons que vous travaillez avec le problème 13/10 - 3/5. Écrivez ce problème de sorte que les deux numérateurs, 13 et 3, et les deux dénominateurs, 10 et 5, soient côte à côte, séparés par un signe moins. Cela vous donne une meilleure vue d`ensemble du problème et facilite la recherche d`une solution.

2. Trouver le plus petit commun multiple. C`est le plus petit multiple de deux nombres. Le LCF de 10 et 5 dans cet exemple est 10.

Notez que le lcm de deux nombres n`est pas toujours l`un des deux nombres. Par exemple, à 3 et 2, le LCF est 6, car il n`y a pas de nombre inférieur à 6 qui est un multiple de chacun des nombres.

3. Réécrire les fractions avec les mêmes dénominateurs. La fraction 13/10 peut rester inchangée car le dénominateur n`a pas changé, mais la fraction 3/5 devient égale à 6/10 car le dénominateur rentre deux fois dans le multiple commun de 10. Maintenant, vous avez égalisé les deux fractions. 3/5 est égal à 6/10, mais avec la différence que ce n`est plus un problème maintenant de soustraire les deux fractions l`une de l`autre.

Donc la nouvelle tâche sera : 13/10 - 6/10.

4. Soustraire les deux numérateurs l`un de l`autre. Donc 13 - 6 = 7. Ne pas soustraire les dénominateurs.

5. Placez le nouveau numérateur au-dessus du nouveau dénominateur (le LCF précédemment calculé) pour la réponse finale. Le nouveau numérateur est 7 et le dénominateur des deux fractions est 10. Donc la réponse finale est 7/10.

6. Vérifie ton travail. Si vous voulez vous assurer que vous avez fait le calcul correctement, il vous suffit d`ajouter la réponse au plus petit nombre pour récupérer le plus grand nombre. Donc à vérifier : 7/10 + 6/10 = 13/10. Vous êtes maintenant prêt.

Méthode 5 sur 6: Soustraire une fraction d`un nombre entier

1. Ecrire le devoir. Supposons que nous ayons le problème suivant : 5 - 3/4. Notez ceci.

2. Convertir le nombre entier en une fraction avec le même dénominateur que la fraction donnée. Faire une fraction du 5 avec le dénominateur 4. Considérons d`abord que 5 est égal à la fraction 5/1. Ensuite, vous multipliez le numérateur et le dénominateur de la nouvelle fraction par 4 pour obtenir deux fractions avec le même dénominateur. Cela garde la valeur de la fraction la même, mais avec des nombres différents. Donc, 5/1 x 4/4 = 20/4.

3. Réécrire le devoir. Cela peut maintenant être écrit comme : 20/4 - 3/4.

4. Soustraire les numérateurs des fractions et garder les fractions égales. Donc, 20 - 3 = 17. Donc le numérateur final devient 17 et le dénominateur est 4.

5. Donc la réponse au problème est 17/4. Pour convertir cette fraction impropre en une fraction composée, divisez 17 par 4 pour obtenir le nombre 4 avec un reste de 1. La réponse ressemble alors à ceci : 4 1/4.

Méthode 6 sur 6 : Soustraction de variables

1. Ecrire le devoir. Supposons que vous travaillez sur le problème suivant : 3x - 5x + 2y - z - (2x + 2x + y). Écris la première équation au-dessus de la seconde.

2. Soustraire tous les termes similaires les uns des autres. Lorsque vous travaillez avec des variables, vous ne pouvez soustraire que des termes avec la même variable et avec la même puissance. Cela signifie que vous pouvez faire 4x -7x, mais pas 4x -7x. Vous pouvez donc diviser cette tâche comme ceci :

3x - 2x = x

-5x - 2x = -7x

2y - y = y

-z - 0 = -z

3. Donnez votre réponse finale. Maintenant que vous avez soustrait tous les termes égaux, vous pouvez immédiatement donner votre réponse finale. Voici la réponse :

3x - 5x + 2y - z - (2x + 2x + y) = x - 7x + y - z

Des astuces

Divisez les plus grands nombres en plus petits morceaux. Prendre : 63 - 25.Personne ne dit que vous devez soustraire les 25 à la fois. Vous pouvez d`abord soustraire 3 pour obtenir 60 ; puis soustrayez 20 pour obtenir 40 puis les 2 derniers. Résultat : 38. Et maintenant tu n`as plus besoin d`emprunter.

Mises en garde

Si vous avez un mélange de nombres positifs et négatifs, les choses deviennent beaucoup plus compliquées.Continuez à chercher des articles qui peuvent vous aider avec cela.