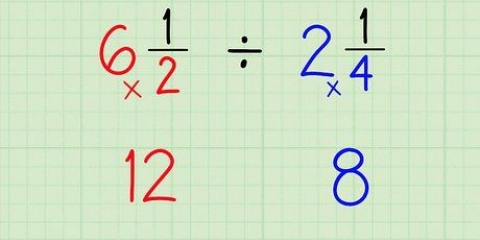Dans l`exercice #1 (5厂65), 5 est le dénominateur et 6 est le premier chiffre du numérateur (65). 5 va une fois dans 6, alors mettez un 1 sur le signe de division, au-dessus du 6. Dans l`exercice #2 (3厂136), 3 (le diviseur) ne rentre pas complètement dans 1 (le premier chiffre du numérateur). Dans ce cas, écrivez un 0 au-dessus du signe de division, au-dessus du 1. 
Dans l`exercice #1 (5厂65), multipliez le nombre au-dessus de la barre (1) par le dénominateur (5), ce qui donne 1x5 = 5, et placez la réponse (5) juste en dessous de 6 sur 65. Dans l`exercice #2 (`3厂136) il y a un zéro au-dessus du signe de division, donc si vous le multipliez par 3 (le dénominateur), le résultat est zéro. Écrivez un zéro sur une nouvelle ligne juste en dessous de 1 sur 136. 
Dans l`exercice #1 (5厂65), soustrayez le 5 (le produit de la nouvelle ligne) du 6 au-dessus (le premier chiffre du numérateur) : 6 - 5 = 1. Placez le résultat (1) dans une autre nouvelle ligne directement en dessous de 5. Dans l`exercice #2 (3厂136) soustraire le 0 (le produit de la nouvelle rangée) du 1 en haut à droite (le premier chiffre du compteur). Placez le résultat (1) dans une autre nouvelle ligne directement en dessous du 0. 
Dans l`exercice #1 (5厂65), abaisser le 5 sur 65 pour qu`il soit à côté du 1 obtenu en soustrayant 5 à 6. Il y en a maintenant 15 dans cette rangée. Dans l`exercice #2 (3厂136), faites tomber le 3 sur 136 et placez-le à côté du 1, vous donnant 13. 
Pour continuer avec 5厂65, diviser le nouveau nombre (15) par 5 (le dénominateur), et écrire le résultat (3, car 15 5 = 3) à droite du 1 au-dessus du signe de division. Ensuite, vous multipliez ce 3 au-dessus du signe de division par 5 (le dénominateur) et écrivez le résultat (15, car 3x5 = 15) moins de 15 ans sous le signe division. Enfin, soustrayez 15 de 15 et écrivez 0 dans une nouvelle ligne du bas. L`exemple du problème n° 1 est maintenant terminé, car il n`y a plus de nombres à réduire au dénominateur. La réponse (13) est au-dessus du signe de division. 
Pour 3厂136: Déterminez combien de fois 3 va complètement dans 13, et écrivez la réponse (4) à droite du 0 au-dessus du signe de division. Multipliez ensuite 4 par 3 et écrivez la réponse (12) sous 13. Enfin, soustrayez 12 de 13 et écrivez la réponse (1) sous 12. 
Pour 3厂136: Continuer le processus pour le tour suivant. Faites tomber le 6 sur 136, en laissant 16 dans la rangée du bas. Divisez 16 par 3 et écrivez le résultat (5) au-dessus du signe de division. Multipliez 5 par 3 et écrivez le résultat (15) dans une nouvelle ligne du bas. Soustrayez 15 de 16 et écrivez le résultat (1) dans une nouvelle ligne du bas. Puisqu`il n`y a plus de chiffres à inclure dans le numérateur, vous avez terminé le problème et le 1 sur la ligne du bas est le reste (le nombre qui reste). Écrivez-le au-dessus du signe de division, éventuellement avec un `r.`avant pour que votre réponse finale `45 r.1` devient. 

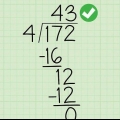
Dans ce problème, 4 (le dénominateur) rentre une fois dans 5 (le premier chiffre du numérateur), avec un reste de 1 (5 4 = 1 r.1). Placez le quotient, 1, au-dessus de la longue ligne de division. Placez un petit 1 en exposant à côté du 5, pour vous rappeler que vous aviez un reste de 1. Le 518 en dessous de la ligne de division devrait maintenant ressembler à ceci : 518. 
Dans le problème, le nombre formé par le reste et le deuxième nombre du numérateur est 11. le dénominateur (4), entre dans 11 deux fois, laissant un reste de 3 (11 4 = 2 r.3) restes. Écrivez le 2 au-dessus de la ligne de division (ce qui vous donne 12) et le 3 en exposant à côté du 1 sur 518. Le compteur d`origine, 518, devrait maintenant ressembler à ceci : 518. 
Dans le problème, 38 est le prochain (et dernier) nombre du numérateur -- le reste 3 de l`étape précédente, et le nombre 8 est le dernier terme du numérateur. Le dénominateur (4) va dans 38 neuf fois avec un reste de 2 (38 4 = 9 r.2), parce que 4 x 9 = 36, qui est deux moins que 38. Écrivez ce dernier reste (2) au-dessus de la ligne de division pour compléter votre réponse. Donc, votre dernière réponse au-dessus du diviseur est 129 r.2.. 

Dans cet exemple de problème, on inversera 5/8 pour que le 8 soit en haut et le 5 soit en bas. 
Par exemple: 3/4 x 8/5. 
Dans ce cas, les numérateurs sont 3 et 8, et 3x8 = 24. 
Les dénominateurs sont 4 et 5 dans le problème, et 4x5 = 20. 
Dans le devoir : 3/4 x 8/5 = 24/20. 
Dans le cas de 24/20, 4 est le plus grand nombre qui va de manière égale dans 24 et 20. Vous pouvez le confirmer en écrivant tous les diviseurs des deux nombres et en choisissant le plus grand nombre qui est un diviseur des deux : 24 : 1, 2, 3, 4, 6, 8, 12, 24 20 : 1, 2, 4, 5, 10, 20 Puisque 4 est le plus grand diviseur commun de 24 et 20, divisez les deux nombres par 4 pour simplifier la fraction. 24/4 = 6 20/4 = 5 24/20 = 6/5. Alors: 3/4 5/8 = 6/5 
Dans le problème, 5 passe dans 6 une fois avec un reste de 1. Donc le nouvel entier est 1, le nouveau numérateur est 1, et le dénominateur reste 5. Le résultat: 6/5 = 1 1/5. 

Dans le devoir : 8 - 5 = 3. 
Ainsi: 3 3 = 3. 

Dans le problème, tout ce que vous avez à faire est de déplacer le point décimal d`une position à la fois pour le dénominateur et le numérateur. Donc : 0,5 devient 5 et 65,5 devient 655. Cependant, si les nombres du problème étaient de 0,5 et 65,55, vous déplaceriez la virgule décimale de deux positions dans 65,55, ce qui en ferait 6555. Par conséquent, vous devez également décaler la virgule décimale de 0,5 à deux positions. Pour ce faire, ajoutez un zéro à la fin et faites-en 50. 
Dans la déclaration, la décimale vient en 655 après les 5 derniers (comme 655,0). Écrivez donc la virgule au-dessus de la ligne de division directement au-dessus de la virgule en 655. 
Divisez le centième (6) par 5. Vous obtenez alors 1, avec le reste 1. Placez 1 à la centième place au-dessus de la longue ligne de division et soustrayez 5 de 6 en dessous du nombre six. Le reste, 1, reste. Abattez les cinq premiers de 655 et vous obtenez le nombre 15. Divisez 15 par 5 et vous obtenez 3. Placez les trois au-dessus du caractère de division longue, à côté du 1. Abattre les 5 derniers. Divisez 5 par 5 et vous obtenez 1 -- placez le 1 au-dessus du caractère de division longue. Il n`y a pas de reste, car 5 va une fois sur 5. La réponse est le nombre au-dessus du signe de division long (131), donc 655 5 = 131. Si vous sortez une calculatrice, vous verrez qu`il s`agit également de la réponse à la division d`origine : 65,5 0,5.
Faire des sommes de division
Teneur
La division est l`une des quatre principales opérations arithmétiques, avec l`addition, la soustraction et la multiplication. En plus des nombres entiers, vous pouvez également diviser des nombres décimaux, des fractions ou des exposants. Vous pouvez faire une division longue ou, si l`un des nombres est un seul chiffre, une division courte. Commencez à maîtriser la division longue, car c`est la clé de toute l`opération.
Pas
Méthode 1 sur 5: Division longue

1. Écrivez le problème à l`aide d`unsigne de longue division. Le signe de la division longue ( ?? ) ressemble à une `fin de parenthèse` avec un nombre en dessous. Placez le dénominateur, le nombre que vous divisez, à l`extérieur du signe de division long et le numérateur, le nombre que vous divisez, à l`intérieur du signe de division long .
- Exemple de problème n°1 (débutant) : 65 5. Placez le 5 à l`extérieur de la division et le 65 à l`intérieur. Cela devrait ressembler 5厂65, mais avec le 65 en dessous de la ligne horizontale.
- Exemple d`exercice #2 (avancé) : 136 3. Placez le 3 à l`extérieur de la division et le 136 à l`intérieur. Cela devrait ressembler 3厂136, mais avec le 136 en dessous de la ligne horizontale.

2. Diviser le premier chiffre du numérateur par le dénominateur. En d`autres termes, découvrez combien de fois le dénominateur (le nombre en dehors du signe de division) entre dans le premier chiffre du numérateur. Placez le résultat entier au-dessus du signe de division, juste au-dessus du premier chiffre du dénominateur.

3. Multipliez le nombre au-dessus du signe de division par le dénominateur. Prenez le nombre que vous avez écrit juste au-dessus de la division et multipliez-le par le dénominateur (le nombre à gauche de la division). Écrivez le résultat dans une nouvelle ligne sous le numérateur, aligné avec le premier chiffre du numérateur.

4. Soustraire le produit (résultat de la multiplication) du premier chiffre du numérateur. En d`autres termes, soustrayez le nombre que vous venez d`écrire dans la nouvelle ligne sous le numérateur du nombre dans le numérateur directement au-dessus. Ecrire le résultat dans une nouvelle ligne, aligné sous les nombres de la soustraction.

5. Abaisser le deuxième chiffre du compteur. Amenez le deuxième chiffre du compteur jusqu`à la nouvelle rangée du bas, juste à droite du résultat de la soustraction que vous venez d`obtenir.

6. Répétez la division longue (tâche #1). Cette fois, utilisez le numérateur (le nombre à gauche du signe de division) et le nouveau nombre sur la rangée du bas (le résultat de votre premier tour de maths et le chiffre que vous avez reporté). Comme précédemment, divisez, multipliez et soustrayez vos nombres, pour obtenir le résultat.

sept. Répétez la division longue (tâche #2). Comme précédemment, commencez par la division, la multiplication puis la soustraction.

8. Faites un autre long tour de division et vous obtenez le reste (tâche #2). Lorsque vous avez terminé avec ce problème, notez qu`il y a un reste (c`est-à-dire un nombre qui reste à la fin de votre calcul). Vous mettez ce repos à côté de votre réponse entière.
Méthode 2 sur 5: Division courte

1. Utilisez un trait d`union pour écrire le problème. Placez le dénominateur, le nombre par lequel vous divisez, à l`extérieur (et à gauche de) la ligne de division. Placez le numérateur, le nombre que vous allez diviser, à l`intérieur (à droite et en dessous) de la ligne de division.
- À partage rapide, le dénominateur peut-il être composé d`un seul chiffre.
- Mission: 518 4. Dans ce cas, le 4 sera à l`extérieur de la ligne de division et 518 sera à l`intérieur.

2. Diviser le premier chiffre du numérateur par le dénominateur. En d`autres termes, déterminez combien de fois le nombre à l`extérieur du diviseur rentre dans le premier chiffre du nombre à l`intérieur du diviseur. Écrivez l`entier du résultat au-dessus de la barre de division et écrivez tout reste en exposant à côté du premier chiffre du numérateur.

3. Divisez le reste et le deuxième chiffre du numérateur par le dénominateur. Traitez le nombre en exposant indiquant le reste comme un chiffre à part entière et combinez-le avec le chiffre du numérateur immédiatement à sa droite. Déterminez combien de fois le dénominateur entre complètement dans ce nouveau nombre à 2 chiffres et écrivez le nombre entier et tout reste comme vous le faisiez auparavant.

4. Répétez ceci jusqu`à ce que vous ayez parcouru tout le compteur. Continuez à déterminer combien de fois le dénominateur entre dans le nombre formé par le chiffre suivant du numérateur et le reste en exposant immédiatement à sa gauche. Une fois que vous avez parcouru tous les chiffres du compteur, vous avez votre réponse.
Méthode 3 sur 5: Division de fractions

1. Écrivez la somme de la division de sorte que les deux fractions soient côte à côte. À diviser des fractions, écrire la première fraction suivie du symbole de division (÷) puis la deuxième fraction.
- Par exemple, la déclaration pourrait être quelque chose comme : 3/4 5/8. Pour plus de commodité, utilisez des lignes horizontales plutôt que diagonales pour séparer le numérateur (numéro du haut) et le dénominateur (numéro du bas) de toute fraction.

2. Inverser le numérateur et le dénominateur de la deuxième fraction. La deuxième fraction devient son propre inverse.

3. Changer la barre de division en signe de multiplication. Pour diviser des fractions, multipliez la première fraction par l`inverse de la seconde.

4. Multiplier les numérateurs des fractions. Suivez la même procédure que pour la multiplication de deux fractions.

5. Multiplier les dénominateurs des fractions de la même manière. Encore une fois, c`est exactement ce que vous feriez pour multiplier deux fractions.

6. Placer le produit des numérateurs au dessus du produit des dénominateurs. Maintenant que vous avez multiplié les numérateurs et les dénominateurs des deux fractions, vous pouvez former le produit des deux fractions.

sept. Simplifier la fraction, si nécessaire. Pour simplifier la fraction, déterminer le plus grand diviseur commun, ou le plus grand nombre qui correspond aux deux nombres dans son intégralité, puis diviser à la fois le numérateur et le dénominateur par ce nombre.

8. Réécrivez la fraction sous forme de nombre fractionnaire, si nécessaire. Pour ce faire, divisez le numérateur par le dénominateur et écrivez la réponse sous forme d`entier. Le reste (le nombre qui reste) est le numérateur de la nouvelle fraction. Le dénominateur de la fraction reste le même.
Méthode 4 sur 5: Diviser les exposants

1. Assurez-vous que les exposants ont la même base. Tu peux diviser les exposants s`ils ont la même base. S`ils n`ont pas la même base, vous devrez les manipuler jusqu`à ce qu`ils le fassent, si vous le pouvez.
- Si vous commencez tout juste avec cela, faites d`abord un problème dans lequel les deux exposants ont déjà la même base. Par exemple: 3 3.

2. Soustraire les exposants les uns des autres. Il suffit de soustraire le deuxième exposant du premier. Ne vous inquiétez pas pour la base pour l`instant.

3. Placez le nouvel exposant au-dessus de la base d`origine. Il suffit d`écrire le nouvel exposant au-dessus de la base d`origine. C`est tout!
Méthode 5 sur 5: Division de nombres décimaux

1. Écrivez le problème avec un trait d`union. Placez le dénominateur, le nombre par lequel vous divisez, à l`extérieur (et à gauche de) la longue barre de division, et le numérateur, le nombre que vous divisez, à l`intérieur de la longue barre de division. À diviser des décimales, convertir d`abord les nombres décimaux en nombres entiers.
- Dans l`exemple 65,5 0,5 est placé 0,5 à l`extérieur de la ligne de division et 65,5 à l`intérieur.

2. Déplacez les points décimaux de manière égale pour créer deux nombres entiers. Faites simplement glisser les points décimaux vers la droite jusqu`à ce qu`ils soient à la fin de chaque nombre. Assurez-vous de les déplacer du même nombre de positions pour chaque nombre -- si vous devez déplacer la virgule décimale de deux positions dans le dénominateur, faites de même pour le numérateur.

3. Placez le point décimal directement au-dessus de la ligne de division. Placez une décimale sur le signe de division longue directement au-dessus de la décimale dans le numérateur.

4. Résoudre le problème en effectuant une division longue. Pour diviser 655 par 5, procédez comme suit :
Articles sur le sujet "Faire des sommes de division"
Оцените, пожалуйста статью
Populaire