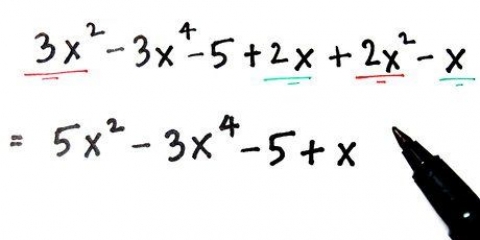Déterminer le troisième angle d'un triangle

Teneur

Pas
Mises en garde

Déterminer le troisième angle d`un triangle si vous savez quels sont les deux autres angles est facile. Il suffit de soustraire les autres angles de 180° pour trouver le troisième angle. Cependant, il existe quelques autres façons de déterminer le troisième angle d`un triangle, en fonction du problème avec lequel vous travaillez. Si vous voulez apprendre à déterminer cet illustre troisième coin d`un triangle, lisez l`étape 1 pour commencer.

Pas

Méthode 1 sur 3: Utilisation des deux autres coins

Image intitulée Trouver le troisième angle d`un triangle Étape 1

1. Additionner les deux angles connus ensemble. Tout ce que vous devez savoir, c`est que tous les angles d`un triangle s`additionnent toujours être à 180°. C`est toujours vrai. Donc, si vous connaissez deux des trois coins du triangle, il ne vous manque qu`une petite pièce du puzzle. La première chose que vous pouvez faire est d`additionner les angles que vous connaissez déjà. Dans cet exemple, les angles que vous connaissez sont 80° et 65°. Additionnez-les (80° + 65°) pour obtenir 145°.

Image intitulée Trouver le troisième angle d`un triangle Étape 2

2. Soustraire ce nombre de 180°. Les angles d`un triangle sont additionnés à 180°. Donc doit l`angle restant avec les autres angles est de 180°. Dans cet exemple : 180° - 145° = 35°.

Image intitulée Trouver le troisième angle d`un triangle Étape 3

3. Écrivez votre réponse. Vous savez maintenant que le troisième angle est de 35°. En cas de doute, il suffit de vérifier votre travail. Les trois angles ensemble doivent être de 180° degrés, sinon ce n`est pas un triangle. 80° + 65° + 35° = 180°. Vous êtes maintenant prêt.

Méthode 2 sur 3: Utilisation de variables

Image intitulée Trouver le troisième angle d`un triangle Étape 4

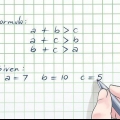
1. Écrivez le problème. Parfois, vous n`avez pas cette chance et vous ne connaissez pas les valeurs des deux angles d`un triangle, mais vous n`avez que quelques variables, ou quelques variables et un angle. Disons que vous avez affaire au problème suivant : Déterminer l`angle `x` du triangle de dimensions `x`, `2x` et 24°. Écrivez simplement ceci d`abord.

Image intitulée Trouver le troisième angle d`un triangle Étape 5

2. Additionner toutes les dimensions ensemble. C`est le même principe que tu suivrais si tu connaissais les deux angles. Il suffit de faire correspondre les valeurs des angles en combinant les variables. Alors, x + 2x + 24° = 3x + 24°.

Image intitulée Trouver le troisième angle d`un triangle Étape 6

3. Soustraire ces valeurs de 180°. Soustrayez ensuite ces valeurs de 180° pour vous rapprocher de la résolution du problème. Assurez-vous que l`équation est égale à 0. Voici à quoi cela ressemble :

180° - (3x + 24°) = 0

180° - 3x - 24° = 0

156° - 3x = 0

Image intitulée Trouver le troisième angle d`un triangle Étape 7

4. Résolvez maintenant pour x. Déplacez maintenant les variables d`un côté de l`équation et les nombres de l`autre. Vous obtenez 156° = 3x. Divisez maintenant les deux côtés de l`équation par 3 pour obtenir x = 52°. Cela signifie que le troisième angle du triangle doit être de 52°. L`autre angle est 2x (2x 52° ou 104°).

Image intitulée Trouver le troisième angle d`un triangle Étape 8

5. Vérifie ton travail. Si vous voulez vous assurer qu`il s`agit d`un triangle valide, ajoutez simplement les trois valeurs des angles ensemble pour voir si elles totalisent 180°. Soit 52° + 104° + 24° = 180°. Vous êtes maintenant prêt.

Méthode 3 sur 3: Utiliser d`autres méthodes

Image intitulée Trouver le troisième angle d`un triangle Étape 9

1. Trouver le troisième angle d`un triangle isocèle. Les triangles isocèles ont deux côtés égaux et deux angles égaux. Les côtés égaux sont chacun marqués d`un signe dièse, qui indique que les angles opposés des deux côtés sont égaux. Si vous connaissez la mesure angulaire d`un angle égal d`un triangle isocèle, alors vous connaissez aussi l`autre angle égal. Vous pouvez le déterminer comme suit :

Si l`un des angles égaux est de 40°, alors vous savez que l`autre angle est également de 40°. Vous pouvez trouver le troisième côté, si nécessaire, en soustrayant 40° + 40° (c`est-à-dire 80°) à 180°. 180° - 80° = 100°, qui est l`angle restant.

Image intitulée Trouver le troisième angle d`un triangle Étape 10

2. Trouver le troisième angle d`un triangle équilatéral. Un triangle équilatéral n`a que des côtés égaux et des angles égaux. Souvent, cela est indiqué par deux marques de hachage au milieu de chacun des côtés. Cela signifie que la valeur de tout angle dans un triangle équilatéral est de 60°. Vérifie ton travail. 60° + 60° + 60° = 180°.

Image intitulée Trouver le troisième angle d`un triangle Étape 11

3. Trouver le troisième angle d`un triangle rectangle. Supposons que vous ayez un triangle rectangle dont les autres angles sont de 30°. Si c`est un triangle rectangle, alors vous savez que l`un des angles est exactement de 90°. Les mêmes principes s`appliquent. Tout ce que vous avez à faire est d`additionner les angles que vous connaissez (30° + 90° = 120°) et de soustraire ce nombre de 180°. En effet, 180° - 120° = 60°. Donc le troisième angle est de 60°.

Mises en garde

Faire une erreur lors de l`addition et de la soustraction doit entraîner une mauvaise réponse. C`est toujours une bonne idée de vérifier votre travail, même s`il ne semble pas faux.